目录
1. 基础知识
2. 大整数 + 大整数
3. 大整数 - 大整数
1. 基础知识
利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。
这里我们要介绍:大整数 + 大整数,大整数 - 大整数,大整数 * 小整数,大整数 / 小整数。
大整数显然用简单的数据类型是无法表示的。所以我们选用数组来存储大整数的每一位。于是,就产生了这么一个问题:数组下标为0的元素是存最高位还是最低位呢?
显然,我们在运算过程中可能会发生进位,这时,如果我们用第一种(下标为0存最高位),在运算过程中最高位发生进位时,就需要在数组的前面添加一个新的位置来存放产生的进位。这就需要将数组的元素整体向后移动,这很麻烦。所以我们选用第二种方式来存储大整数(下标为0存最低位),这样在产生进位时我们只需要在数组的后面添加一个位置即可。这是非常容易滴。
2. 大整数 + 大整数
我们可以从人类计算加法的方法中找出做加法的规律:
下面以 345678 + 6789 距离分析:我们将存储进位的变量 carry 初始化为0,然后让 carry 去与两个大整数的个位相加,即 0 + 8 + 9 = 17,将得到的结果 17 对 10 取模,得到相加后的个位:7,push_back到存放结果的数组,然后继续将相加后的结果17除以10,作为下一位相加的进位。依次类推,直到将两个大整数的每一位相加。
#include<iostream>
#include<vector>
using namespace std;
//传引用可以提高效率,不用copy一遍数组了
vector<int> add(vector<int>& A, vector<int>& B)
{
//存放结果的数组
vector<int> C;
//用来记录进位的变量,初始化为0
int carry = 0;
//对两个大整数的对应位置的数相加
for (int i = 0; i < A.size() || i < B.size(); i++)
{
//因为两个大整数的长度可能有差异,当一个大整数的每一位加完了,就不需要继续了
if (i < A.size())
carry += A[i];
if (i < B.size())
carry += B[i];
C.push_back(carry % 10);
carry /= 10;
}
//如果最高位相加有进位(只可能是1,push_back 1 也行),再将进位push_back
if (carry)
{
C.push_back(carry);
}
return C;
}
void test01()
{
//两个大整数以字符串的形式输入
string a, b;
cout << "请输入两个整数,以回车键结束" << endl;
cin >> a >> b;
//两个数组用来存放大整数的每一位
vector<int> A, B;
//将输入的大整数的每一位拆分后添加到数组
//数字字符 - '0' 即可得到数字字符对应的数字
for (int i = a.size() - 1; i >= 0; i--)
{
A.push_back(a[i] - '0');
}
for (int i = b.size() - 1; i >= 0; i--)
{
B.push_back(b[i] - '0');
}
//用一下大整数加法的接口,并且用C接收最终结果
vector<int>C = add(A, B);
cout << "相加的结果:";
//输出结果
for (int i = C.size() - 1; i >= 0; i--)
{
printf("%d", C[i]);
}
cout << endl;
}
int main()
{
//大整数的加法
test01();
system("pause");
return 0;
}3. 大整数 - 大整数
大整数减去大整数用户可能输入的是一个较小的大整数减去一个较大的大整数,我们就需要先进行一个比较,确保我们在做减法时是大的数减去小的数,如果需要在最终的结果上加上负号即可。
与大整数加大整数类似,对两个大整数的每一位做减法,显然这时有两种情况:当减数小于被减数,此时就需要向前借一位,而当减数大于等于被减数则不需要进位。
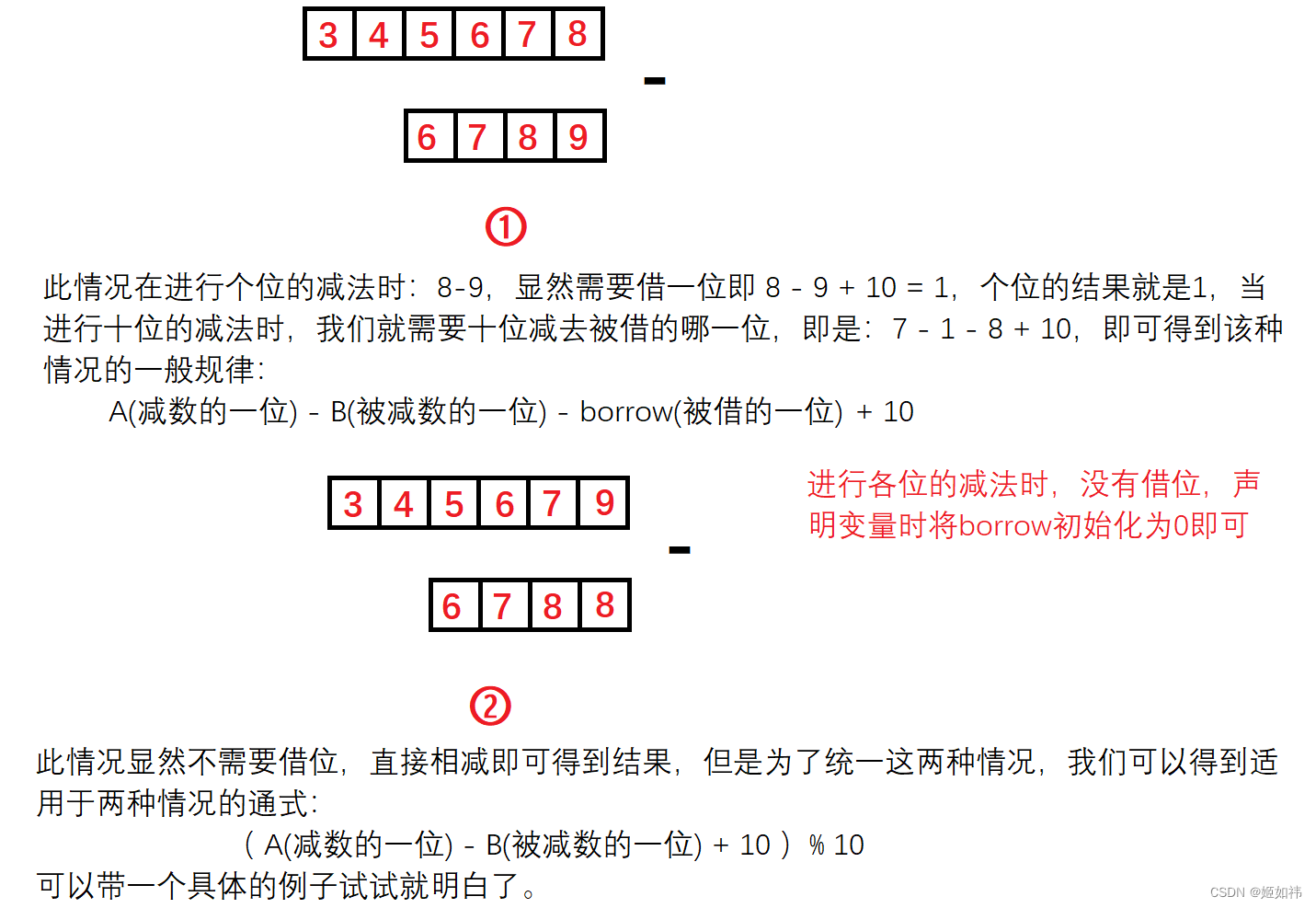
这里还有一个问题就是:相减的结果在打印时可能会有先导0,例如:12345 - 12300 在没有去掉先导0,得到的结果就是:00045,这显然不是我们想要的。我们需要对存放结果的数组的最后一个元素进行判断,如果该元素为0,就需要将其pop掉。但是如果相减的最终结果是0,这样做存放结果的数组里面将没有元素了,所以我们需要保证存放结果的数组中至少有一个元素。
bool cmp(vector<int>& A, vector<int>& B)
{
//先比较两整数的长度
if (A.size() != B.size())
{
return A.size() - B.size();
}
//从最高位开始比较
for (int i = A.size() - 1; i >= 0; i--)
{
if (A[i] != B[i])
return A[i] > B[i];
}
//这里代表两个数相等
return true;
}
vector<int> sub(vector<int>& A, vector<int>& B)
{
vector<int> C;
int borrow = 0;
for (int i = 0; i < A.size(); i++)
{
//减数减去借位
borrow = A[i] - borrow;
//当i不小于被减数的大小就不用做减法了
if (i < B.size())
borrow -= B[i];
//利用一般规律push_back结果
C.push_back((borrow + 10) % 10);
//有借位borrow置为1
if (borrow < 0)
borrow = 1;
else
borrow = 0;
}
//去掉先导0
while (C.size() > 1 && C.back() == 0)
{
C.pop_back();
}
return C;
}
void test02()
{
//两个大整数以字符串的形式输入
string a, b;
cout << "请输入两个整数,以回车键结束" << endl;
cin >> a >> b;
//两个数组用来存放大整数的每一位
vector<int> A, B;
//将输入的大整数的每一位拆分后添加到数组
//数字字符 - '0' 即可得到数字字符对应的数字
for (int i = a.size() - 1; i >= 0; i--)
{
A.push_back(a[i] - '0');
}
for (int i = b.size() - 1; i >= 0; i--)
{
B.push_back(b[i] - '0');
}
//对两个大整数做判断,确保是大数 - 小数
if (cmp(A, B))
{
//用一下大整数加法的接口,并且用C接收最终结果
vector<int>C = sub(A, B);
cout << "相减的结果:";
//输出结果
for (int i = C.size() - 1; i >= 0; i--)
{
printf("%d", C[i]);
}
cout << endl;
}
else
{
//用一下大整数加法的接口,并且用C接收最终结果
//如果B > A,交换位置传参即可,最后输出数据的时候加上负号
vector<int>C = sub(B, A);
cout << "相减的结果:";
//输出结果
cout << "-";
for (int i = C.size() - 1; i >= 0; i--)
{
printf("%d", C[i]);
}
cout << endl;
}
}
int main()
{
//大整数的减法
test02();
system("pause");
return 0;
}