摘要

剑指 Offer 48. 最长不含重复字符的子字符串

一、滑动窗口解析

这样一来，我们就可以使用「滑动窗口」来解决这个问题了：

我们使用两个指针表示字符串中的某个子串（或窗口）的左右边界，其中左指针代表着上文中枚举子串的起始位置，而右指针即为上文中的 rk；
在每一步的操作中，我们会将左指针向右移动一格，表示我们开始枚举下一个字符作为起始位置，然后我们可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后，这个子串就对应着以左指针开始的，不包含重复字符的最长子串。我们记录下这个子串的长度；
在枚举结束后，我们找到的最长的子串的长度即为答案。

判断重复字符：在上面的流程中，我们还需要使用一种数据结构来判断是否有重复的字符，常用的数据结构为哈希集合。在左指针向右移动的时候，我们从哈希集合中移除一个字符，在右指针向右移动的时候，我们往哈希集合中添加一个字符。

package sliding;

import org.junit.Test;

import java.util.HashSet;
import java.util.Set;

/**
 * @Classname JZ48最长不含重复字符的子字符串
 * @Description TODO
 * @Date 2023/2/18 14:15
 * @Created by xjl
 */
public class JZ48最长不含重复字符的子字符串 {

    public int lengthOfLongestSubstring(String s) {
        // 哈希集合，记录每个字符是否出现过
        Set<Character> set = new HashSet<Character>();
        int n = s.length();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = -1, ans = 0;
        // 在这个就是左指针 从0到n
        for (int left = 0; left < n; ++left) {
            if (left != 0) {
                // 左指针向右移动一格，移除一个字符
                set.remove(s.charAt(left - 1));
            }
            while (rk + 1 < n && !set.contains(s.charAt(rk + 1))) {
                // 不断地移动右指针
                set.add(s.charAt(rk + 1));
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = Math.max(ans, rk - left + 1);
        }
        return ans;
    }


    @Test
    public void test(){
        int abcabcbb = lengthOfLongestSubstring("abcabcbb");

    }
}

复杂度分析

时间复杂度：O(N)，其中N是字符串的长度。左指针和右指针分别会遍历整个字符串一次。
空间复杂度：O(∣Σ∣)，其中Σ表示字符集（即字符串中可以出现的字符），∣Σ∣表示字符集的大小。

二、双指针 + 哈希表

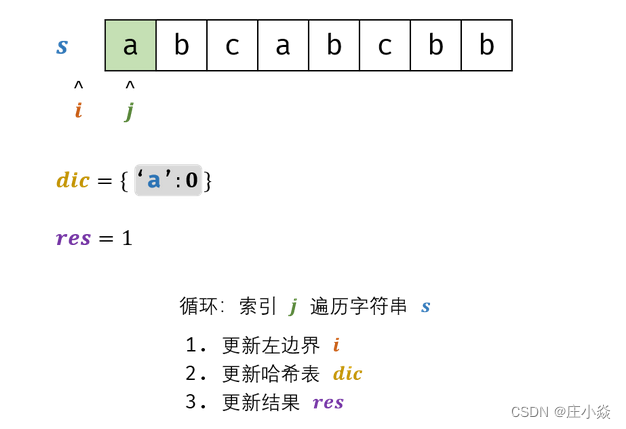
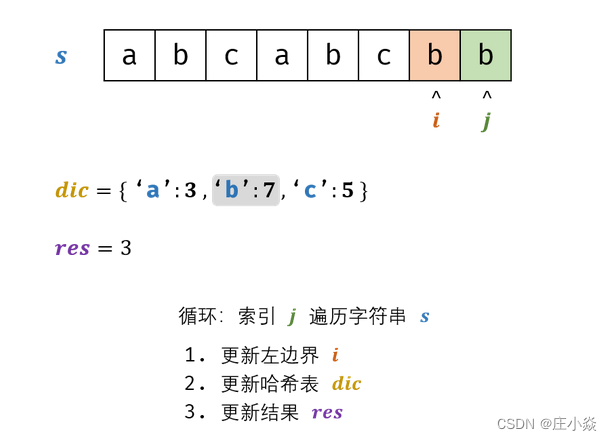
哈希表dic统计:指针 j遍历字符s ，哈希表统计字符s[j] 最后一次出现的索引。
更新左指针i: 根据上轮左指针i和 dic[s[j]]，每轮更新左边界i，保证区间 [i+1,j] 内无重复字符且最大。i=max（dic[s[j]],i）
新结果 res ：取上轮 res和本轮双指针区间 [i+1,j]的宽度(即 j−i)中的最大值。res=max(res,j-i)；

    public int lengthOfLongestSubstring2(String s) {
        Map<Character, Integer> dic = new HashMap<>();
        int left = -1, res = 0;
        for (int right = 0; right < s.length(); right++) {
            if (dic.containsKey(s.charAt(right))) {
                left = Math.max(left, dic.get(s.charAt(right))); // 更新左指针 i
            }
            dic.put(s.charAt(right), right); // 哈希表记录
            res = Math.max(res, right - left); // 更新结果
        }
        return res;
    }

复杂度分析：