ccc-pytorch-回归问题（1）

news2024/9/25 10:37:11

文章目录

- - 1.简单回归实战：
  - 2.手写数据识别

1.简单回归实战：

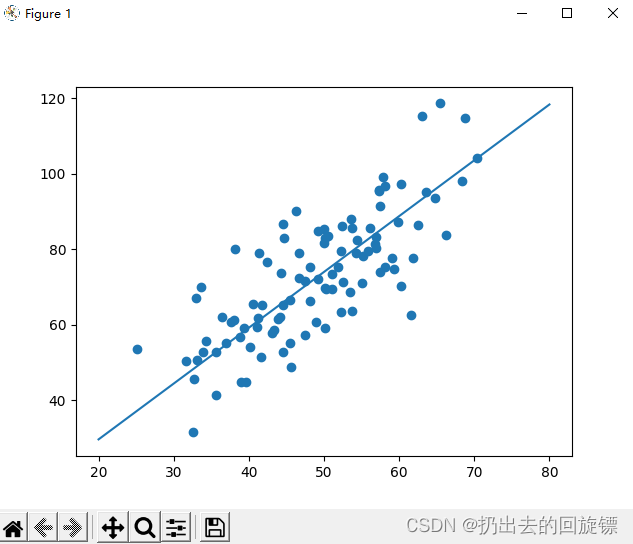
用线性回归拟合二维平面中的100个点
在这里插入图片描述
公式： $y = w x + b$
损失函数： $\sum(y_{really}-y)^2$
迭代方法：梯度下降法，其中 $w$ , $b$ 更新公式如下：
$w_{N+1}=w_N-\eta*\frac{\partial loss}{\partial w}\\ b_{N+1}=b_{N}-\eta*\frac{\partial loss}{\partial b}$
其中 $\eta$ 表示学习率， $\partial$ 表示微分
$\frac{\partial loss}{\partial w}=2(wx+b-y)x/n\\ \frac{\partial loss}{\partial b}=2(wx+b-y)/n$
项目文件：
计算损失函数：

def compute_loss(b,w,points):
    total = 0
    for i in range(0,len(points)):
        x = points[i,0]
        y = points[i,1]
        total += (y-(w*x+b)) ** 2
    return total / float(len(points))

梯度下降迭代更新：

def gradient(b,w,points,leanrningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0,len(points)):
        x = points[i,0]
        y = points[i,1]
        b_gradient += (2/N) * (((w * x)+b)-y)
        w_gradient += (2/N) * (((w * x)+b)-y) * x
    new_b = b - (leanrningRate * b_gradient)
    new_w = w - (leanrningRate * w_gradient)
    return [new_b , new_w]

def graient_descent_runner(points, b, w, learning_rate, num_iterations):
    new_b = b
    new_w = w
    for i in range(num_iterations):
        new_b, new_w = gradient(new_b, new_w, np.array(points), learning_rate)
    return [new_b, new_w]

主函数运行以及绘图结果：

def run():
    points = np.genfromtxt("data.csv",delimiter=",")
    learning_rate = 0.0001
    initial_b = 0
    initial_w = 0
    num_iteractions = 1000
    print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
          .format(initial_b,initial_w,
                  compute_loss(initial_b,initial_w,points)))
    print("Runing...")
    [b, w] = graient_descent_runner(points,initial_b,initial_w,learning_rate,num_iteractions)
    print("After {0} iterations b = {1}, w = {2}, error = {3}".
          format(num_iteractions,b,w,
                 compute_loss(b,w,points)))
    x = np.linspace(20, 80, 5)
    y = w * x + b
    pyplot.plot(x, y)
    pyplot.scatter(points[:, 0], points[:, 1])
    pyplot.show()

if __name__ == '__main__':
    run()

在这里插入图片描述

2.手写数据识别

工具函数库：

import torch
from matplotlib import pyplot as plt

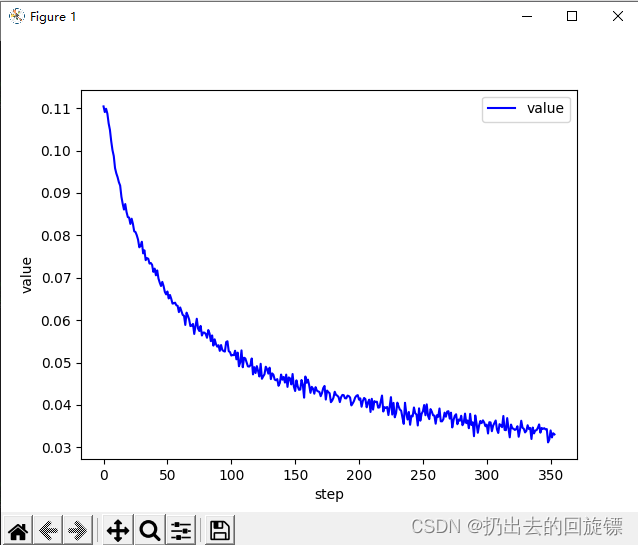
def plot_curve(data):
    fig = plt.figure()
    plt.plot(range(len(data)), data, color='blue')
    plt.legend(['value'], loc='upper right')
    plt.xlabel('step')
    plt.ylabel('value')
    plt.show()

def plot_image(img, label, name):
    fig = plt.figure()
    for i in range(6):
        plt.subplot(2, 3, i + 1)
        plt.tight_layout()
        plt.imshow(img[i][0]*0.3081+0.1307, cmap='gray', interpolation='none')
        plt.title("{}: {}".format(name, label[i].item()))
        plt.xticks([])
        plt.yticks([])
    plt.show()

def one_hot(label, depth=10):
    out = torch.zeros(label.size(0), depth)
    idx = torch.LongTensor(label).view(-1, 1)
    out.scatter_(dim=1, index=idx, value=1)
    return out

第一步：导入库和图像数据

import torch
from torch import nn #构建神经网络
from torch.nn import functional as F 
from torch import optim #最优化工具
import torchvision #视觉工具
from utils import plot_image, plot_curve, one_hot

batch_size = 512
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=True, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=True)

test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=False)

x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), y.min())
plot_image(x, y, 'image sample')

在这里插入图片描述
第二步：新建一个三层的非线性的网层

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        #第一层（28*28是图片，256根据经验随机决定）
        self.fc1 = nn.Linear(28 * 28, 256)
        self.fc2 = nn.Linear(256, 64)
         #第三层(十分类输出一定是10)
        self.fc3 = nn.Linear(64, 10)

    def forward(self, x):
        # x: [b, 1, 28, 28]
        # h1 = relu(xw1+b1) h2 = relu(h1w2+b2) h3 = h2w3+b3
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)

        return x

第三步：train训练

net = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
train_loss = []

for epoch in range(3):
    for batch_idx, (x, y) in enumerate(train_loader):
        # x: [b, 1, 28, 28], y: [512]
        # [b, 1, 28, 28] => [b, 784]，将整个图片看做特征向量
        x = x.view(x.size(0), 28*28)
        # => [b, 10]
        out = net(x)
        # [b, 10]
        y_onehot = one_hot(y)
        # loss = mse(out, y_onehot)
        loss = F.mse_loss(out, y_onehot)
        optimizer.zero_grad()
        loss.backward()#梯度下降
        # w' = w - lr*grad
        optimizer.step()

        train_loss.append(loss.item())
        if batch_idx % 10==0:
            print(epoch, batch_idx, loss.item())

plot_curve(train_loss)

在这里插入图片描述
第四步：准确度测试

total_correct = 0
for x,y in test_loader:
    x  = x.view(x.size(0), 28*28)
    out = net(x)
    # out: [b, 10] => pred: [b]
    pred = out.argmax(dim=1)
    correct = pred.eq(y).sum().float().item()
    total_correct += correct

total_num = len(test_loader.dataset)
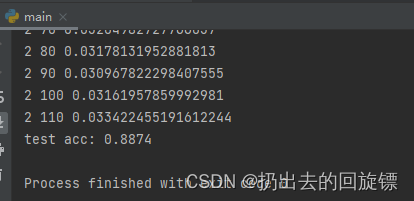
acc = total_correct / total_num
print('test acc:', acc)

x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')

在这里插入图片描述

无注释代码：

import torch
from torch import nn
from torch.nn import functional as F
from torch import optim
import torchvision
from utils import plot_image, plot_curve, one_hot

batch_size = 512
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=True, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=True)

test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=False)

x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), y.min())
plot_image(x, y, 'image sample')

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(28 * 28, 256)
        self.fc2 = nn.Linear(256, 64)
        self.fc3 = nn.Linear(64, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)

        return x

net = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
train_loss = []

for epoch in range(3):
    for batch_idx, (x, y) in enumerate(train_loader):
        x = x.view(x.size(0), 28*28)
        out = net(x)
        y_onehot = one_hot(y)
        loss = F.mse_loss(out, y_onehot)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        train_loss.append(loss.item())
        if batch_idx % 10==0:
            print(epoch, batch_idx, loss.item())

plot_curve(train_loss)

total_correct = 0
for x,y in test_loader:
    x  = x.view(x.size(0), 28*28)
    out = net(x)
    pred = out.argmax(dim=1)
    correct = pred.eq(y).sum().float().item()
    total_correct += correct

total_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)

x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')