DFS深度优先搜索

递归三要素

递归的定义
递归的拆解
递归的出口

什么时候使用DFS？

深度回溯问题（DFS与回溯区别不大）
二叉树问题
组合、排列问题
找方案问题（解空间是一棵树或者图，需要自行构造图/树）
图的搜索问题/路径/方案/节点的的排列

不要使用DFS的场景

连通块问题
拓扑排序
一切可以使用BFS解决的问题

组合问题

例如，[1,2,3] 的所有组合为 [] [1] [2] [3] [1,2] [1,3] [2,3] [1,2,3] 共8种。
- 问题模型：求出所有满足条件的组合
- 判断条件：组合中的元素与顺序无关
- 时间复杂度：2^n
- 难点：将题目的要求构成图或者树，以本题为例，可以将集合中的元素作为节点，那么如何构建边呢？为了避免出现出现12和21这种重复集合，可以让小数节点指向大数节点形成有向边。如下图所示：
除此之外也可以将其构建成一棵树，小节点指向大节点，如下所示：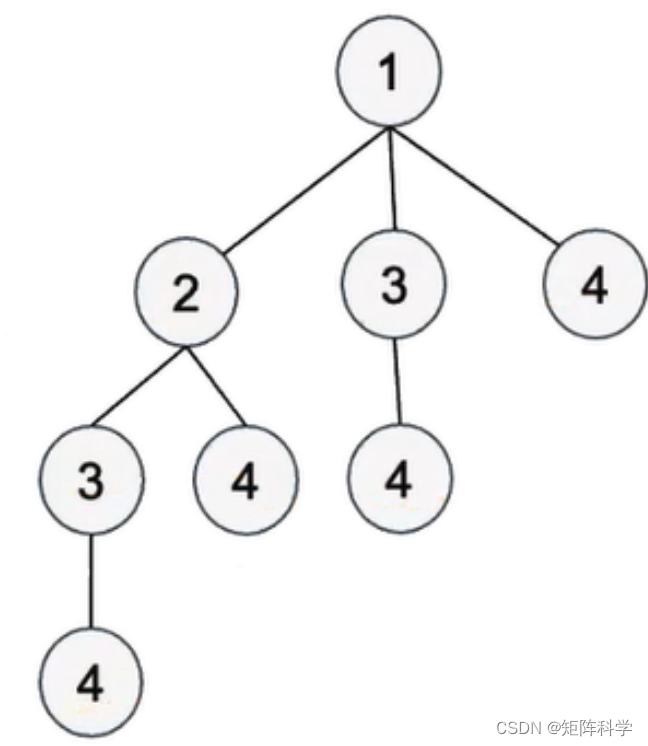

DFS关键模板

    public int def(int x, int y ,int step){
        if(递归出口/达到目标状态){
            //进行对应操作
            return 0;
        }
        for (int i = 0; i < n; i++) {
            //遍历剩下的所有的情况
            if(visit[i]==0){
                //未访问
                x = 下一步更新;
                y = 下一步更新;
                visit[i] = 1;
                def(x,y,step);
                visit[i] = 0;  //记得回溯还原
            }
        }
    }

46. 全排列

class Solution {
    int n;
    List<List<Integer>> res;
    int[] visit;
    int[] permu;

    public void dfs(int[] nums,int step){
        if(step==n){ //存了10个数达到结束条件
            List<Integer> arr = new ArrayList<>();
            for(int a:permu){
                arr.add(a);
            }
            res.add(arr);
            return ;
        }

        for (int i = 0; i < nums.length; i++) {
            if(visit[i]==0){
                permu[step] = nums[i];
                visit[i] = 1;
                dfs(nums,step+1);
                visit[i] = 0;  //记得回溯
            }
        }

    }
    public List<List<Integer>> permute(int[] nums) {
        n = nums.length;
        res = new ArrayList<>();
        visit = new int[n]; 
        permu = new int[n]; //存一个结果
        dfs(nums,0); //0表示permu中存了0个数
        return res;
    }
}

以下题目DFS不一定是好的解法，但是练手深搜是非常合适的。所有，很多时候，其实DFS属于暴力搜索算法，并不是优化算法，但是作为最基础的搜索算法，必须掌握才能在此基础上进行动态规划或者剪枝优化。

386. 字典序排数

class Solution {
    int[] item;
    int[] visit;
    List<Integer> res;

    public void dfs(int[] nums,int step,int n){
        if(step==n){
            for(int a : item){
                res.add(a);
            }
            return;
        }

        for (int i = 0; i < n; i++) {
            if(visit[i]==0){
                visit[i]=1;
                item[step] = nums[i];
                //多了这段中途判断而已
                if(step>0 && ((item[step-1]+"").compareTo(item[step]+""))>0){
                    visit[i]=0;
                    return;
                }  
                dfs(nums,step+1,n);
                visit[i]=0;
            }
        }
    }
    public List<Integer> lexicalOrder(int n) {
        item = new int[n];
        visit = new int[n];
        res = new ArrayList<Integer>();
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i]=i+1;
        }
        dfs(arr,0,n);
        return res;
    }
}

64. 最小路径和

这是一道非常非常典型的题目，DFS如果要求一个数，例如路径条数、方案数、路径总和等等。需要弄清楚，这个变量作为参数传递还是定义一个变量。如果作为参数传递，就是模板，直接在参数上进行加减操作，不影响该值在此循环的值。如果作为单独变量（第二种解法）需要复原变量，需要 sum -= grid[i+1][j] 复原，或者记录前面的值直接用，两种方法都一样。特别推荐直接将其作为参数进行传递。

import org.junit.Test;
import java.util.List;
public class lc64 {
    int res;
    int sum;
    int visit[][];
//==================第一种写法==================
    public void dfs(int[][] grid,int i,int j,int summ){
        if(i==(grid.length-1) && j==grid[0].length-1){
            res = Math.min(res,summ);
        }
        //下走
        if((i+1)<grid.length && visit[i+1][j]==0){
            visit[i+1][j]=1;  
            dfs(grid,i+1,j,summ+grid[i+1][j]);
            visit[i+1][j]=0; 
        }
        //右走
        if((j+1)<grid[0].length && visit[i][j+1]==0){
            visit[i][j+1]=1;  
            dfs(grid,i,j+1,summ+grid[i][j+1]);
            visit[i][j+1]=0; 
        }
    }

//================第二种写法================
    public void dfs(int[][] grid,int i,int j ){
        if(i==(grid.length-1) && j==grid[0].length-1){
            res = Math.min(res,sum);
        }
        //下走
        if((i+1)<grid.length && visit[i+1][j]==0){
            visit[i+1][j]=1;
            int temp = sum;
            sum += grid[i+1][j];
            dfs(grid,i+1,j );
            visit[i+1][j]=0;
            //或者 sum -= grid[i+1][j];
            sum = temp; // 还原sum; 
        }

        //右走
        if((j+1)<grid[0].length && visit[i][j+1]==0){
            visit[i][j+1]=1;
            int temp = sum;
            sum += grid[i][j+1];
            dfs(grid,i,j+1 );
            visit[i][j+1]=0;
            //或者 sum -= grid[i][j+1];
            sum = temp;// 还原sum;
        }
    }

    public int minPathSum(int[][] grid) {
        visit = new int[grid.length][grid[0].length];
        res = Integer.MAX_VALUE;
        sum = grid[0][0] ;
        dfs(grid,0,0 );
        return res;
    } 
}

其实，这道题也是非常好的记忆化搜索的动态规划例题，如下：

class Solution {
    int mem[][];
    public int arrive(int[][] grid,int i,int j){
        if(i==0 && j==0){
            return grid[i][j];
        }

        int v1 = Integer.MAX_VALUE;
        int v2 = Integer.MAX_VALUE;

        if((i-1)>=0 && j>=0 ) {
            if(mem[i-1][j]==-1){
                v1 = arrive(grid,i-1,j);
                mem[i-1][j] = v1;
            }else {
                v1 = mem[i-1][j];
            }
        }
        if((j-1>=0) && i>=0){
            if (mem[i][j-1]==-1){
                v2 = arrive(grid,i,j-1);
                mem[i][j-1] = v2;
            }else{
                v2 = mem[i][j-1];
            }
        }
        return Math.min(v1,v2)+grid[i][j];
    }

    public int minPathSum(int[][] grid) {  
        //动态规划
        mem = new int[grid.length][grid[0].length];
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                mem[i][j] = -1;
            }
        }
        mem[0][0] = grid[0][0];
        return arrive(grid,grid.length-1,grid[0].length-1);

    }
}

最后以一道典型DFS题结束本章讲解

200. 岛屿数量

思路：凡是搜到了一个1，就找到了一个岛屿，为了避免重复计算，需要把这个岛（这个岛不是这个图）的所有1改成0，然后继续往下搜。简单说就是看见1就计数+1，然后把这片岛毁了，接着往下走！其实这里不用visit记录是否访问过，因为访问过的会将其标记为0，但是写了无妨！建议按照模板操作！

public class lc200 {
    int visit[][];
    public void dfs(char[][] grid,int i , int j){
        if(grid[i][j]=='0'){
            //如果是水就不用深入查找了
            return;
        }
        grid[i][j]='0'; //摧毁
        int[][] dirc = new int[][]{{-1,0},{1,0},{0,-1},{0,1}}; //方向 上下左右

        for (int k = 0; k < dirc.length; k++) { //往四个方向走
            int x = dirc[k][0];
            int y = dirc[k][1];
            //往x,y指定的方向走，判断符合条件才走
            if((((i+x)<grid.length)&&(i+x)>=0) &&
                    (((j+y)<grid[0].length) && j+y>=0) &&
                    visit[i+x][j+y]==0){ //这里判断写的复杂，就是边界判断加访问判断

                visit[i+x][j+y] = 1;
                if(grid[i+x][j+y]=='1'){
                    dfs(grid,i+x,j+y); //如果还是岛就继续深入
                }
                visit[i+x][j+y] = 0;
            }
        }
    }
    public int numIslands(char[][] grid) {
        int count = 0;
        visit = new int[grid.length][grid[0].length];
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if(grid[i][j]=='1'){
                    count++;
                    dfs(grid,i,j); //开始毁灭这个岛所有1
                }
            }
        }
        return count;
    }
}