这一篇分享一道在数组中寻找峰值的题目,使用到分而治之,二分查找等思想。本文章会讲解这个二分查找的本质,以及为什么要用二分查找,它能解决哪一类题目?
目录:
一.题目及其要求
1.分而治之
2.题目思路
3.具体做法+配图演示
4.复杂度分析
二.剖析二分查找
1.本质
2.优点
3.适用场景
一.题目及其要求
1.给定一个长度为n的数组,返回其中任何一个峰值的索引
2.峰值元素是指其值严格大于左右相邻值的元素
3.数组两个边界可以看成是最小, nums[−1]= nums[ n]=−∞
4.峰值不存在平的情况,即相邻元素不会相等
5.峰值从第二个数开始,不考虑边界的-∞
如输入[2,4,1,2,7,8,4]时,会形成两个山峰,一个是索引为1,峰值为4的山峰,另一个是索引为5,峰值为8的山峰,如下图所示:
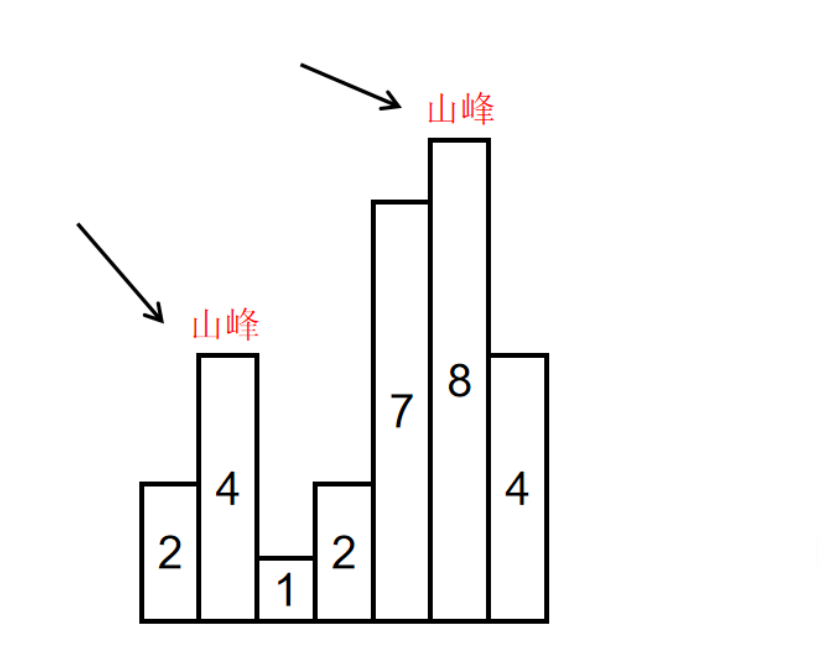
示例:
输入:[2,4,1,2,7,8,4]
返回值:1 说明:4和8都是峰值元素,返回4的索引1或者8的索引5都可以
输入:[1,2,3,1]
返回值:2 说明:3 是峰值元素,返回其索引 2
1.分而治之
分治即“分而治之”,意思就是把一个复杂大问题分成若干个简单的小问题,当小问题解决后,大问题也就迎刃而解。“分”指的是将一个大而复杂的问题划分成多个性质相同但是规模更小的子问题,子题继续按照这样划分,直到问题可以被轻易解决;“治”指的是将子问题单独进行处理。经过分治后的子问题,将若干个子问题进行合并才能得到原问题的解,因此整个分治过程经常用递归来实现。
2.题目思路
因为题目只需要找到其中一个波峰,因此不断地往高处走,一定会有波峰。那我们可以每次找一个标杆元素,将数组分成两个区间,每次就较高的一边走,因此也可以用分治来解决,而标杆元素可以选择区间中点。
//右边是往下,不一定有坡峰
if(nums[mid] > nums[mid + 1])
right = mid;
//右边是往上,一定能找到波峰
else
left = mid + 1;下面配图进行理解上面代码:
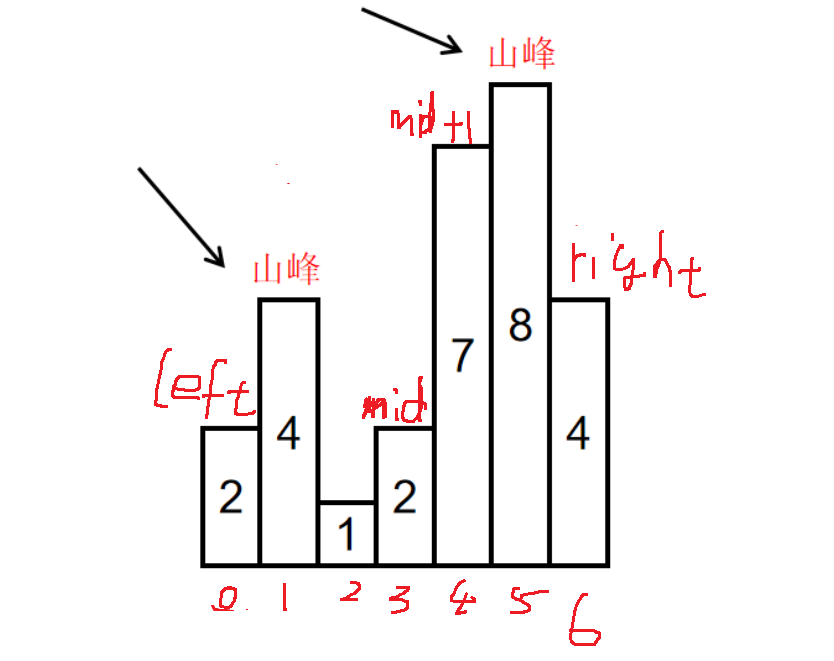
3.具体做法+配图演示
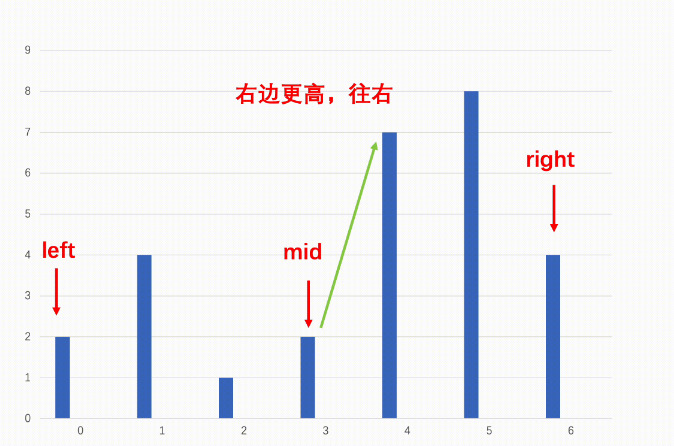
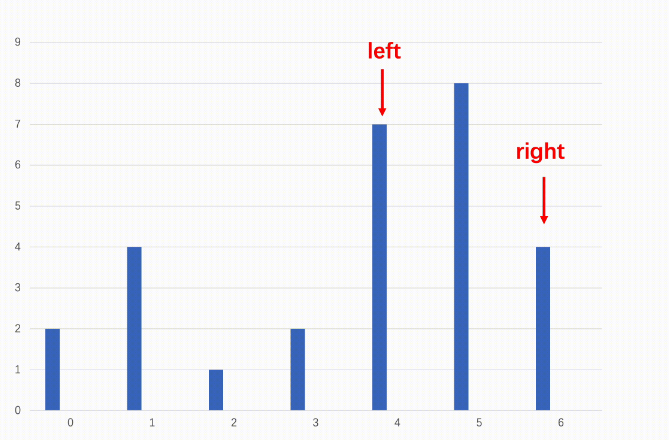
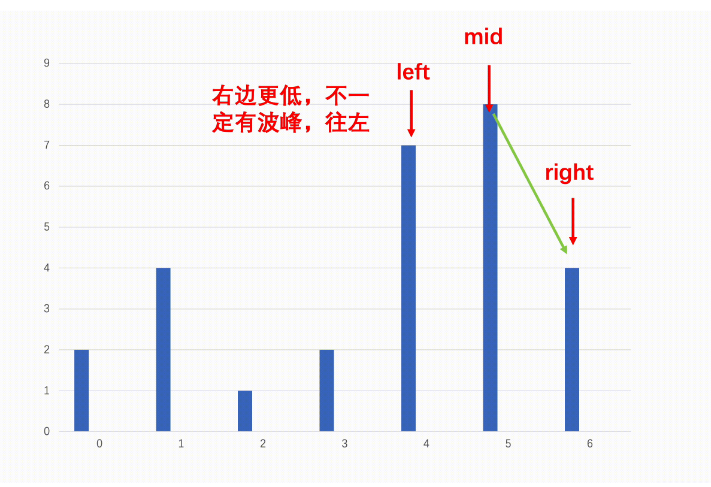
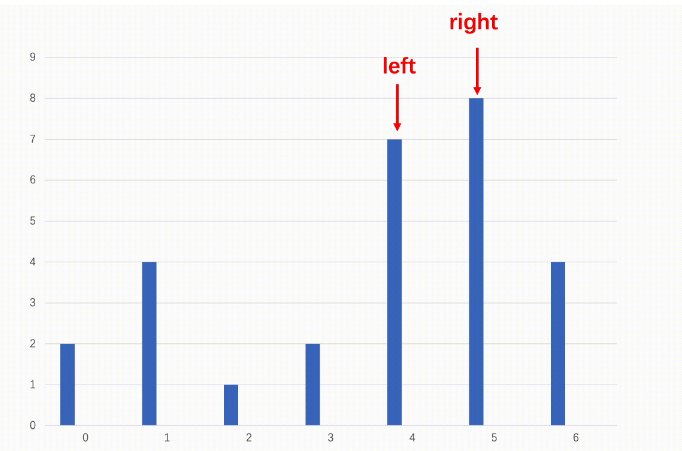
1:二分查找首先从数组首尾开始,每次取中间值,直到首尾相遇。
2:如果中间值的元素大于它右边的元素,说明往右是向下,我们不一定会遇到波峰,但是那就往左收缩区间。
3:如果中间值大于右边的元素,说明此时往右是向上,向上一定能有波峰,那我们往右收缩区间。
4:最后区间收尾相遇的点一定就是波峰。
下面是配图演示:


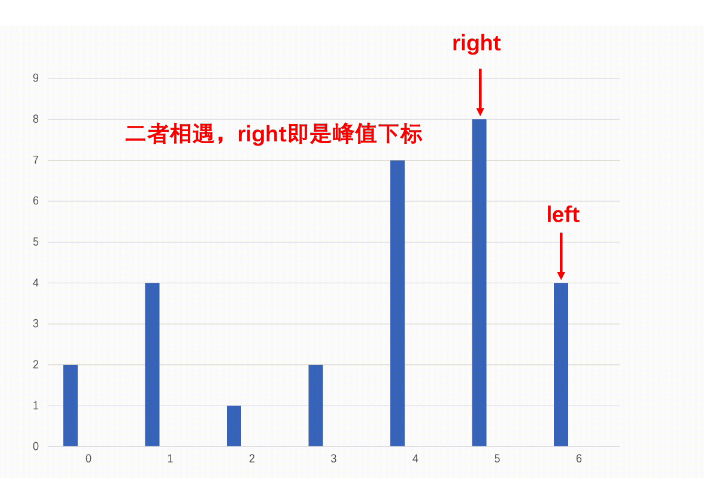
4.代码实现
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
//二分法
while(left < right){
int mid = (left + right) / 2;
//右边是往下,不一定有坡峰
if(nums[mid] > nums[mid + 1])
right = mid;
//右边是往上,一定能找到波峰
else
left = mid + 1;
}
//其中一个波峰
return right;
}
};
4.复杂度分析
时间复杂度:O(log2n),二分法最坏情况对整个数组连续二分,最多能分log2n次。
空间复杂度:O(1),常数级变量,无额外辅助空间。
二.剖析二分查找
1.本质
二分查找的本质是二段性,二分查找的过程本质是对可行区间的压缩。只要满足二段性的问题都可以用二分查找解决。
2.优点
通过对有序数组进行逐步缩小范围的操作,将查找时间从线性时间降低到了对数时间,因此它是一种非常高效的搜索算法。
3.适用场景
二分查找的时间复杂度为O(log n),比其他搜索算法的复杂度要低得多,因此它被广泛应用于各种搜索场景中。
在这里二段性的体现是峰值的左边单调增,右边单调减。你可能会反驳给我们的数值不只有一个峰值,但是只要我们控制好条件,一定可以把范围压缩到只有一个峰值的情况,来看看该怎么处理:
nums[mid] < nums[mid + 1]说明在“上坡”,则可以使left = mid + 1(因为mid肯定不是峰值),向“峰”处压缩
nums[mid] > nums[mid + 1]说明在“下坡”,则应该使right = mid(mid可能是峰值),往“峰”处压缩
虽然开始left和right之间可能有多个峰值,但是随着left和right不断逼近,最后两者之间一定会压缩到一个峰值上,因为两者都是向“峰”不断靠近的,但是不会超过最终的“峰”。
望上文对你有帮助,谢谢你的阅览,后面会持续分享算法题目,大家可以关注一下。
2023.02.18
From:努力进大厂的新青年