在日常生活中,我们经常使用这些术语。但是在统计学和机器学习上下文中使用时,有一个本质的区别。本文将用理论和例子来解释概率和似然之间的关键区别。
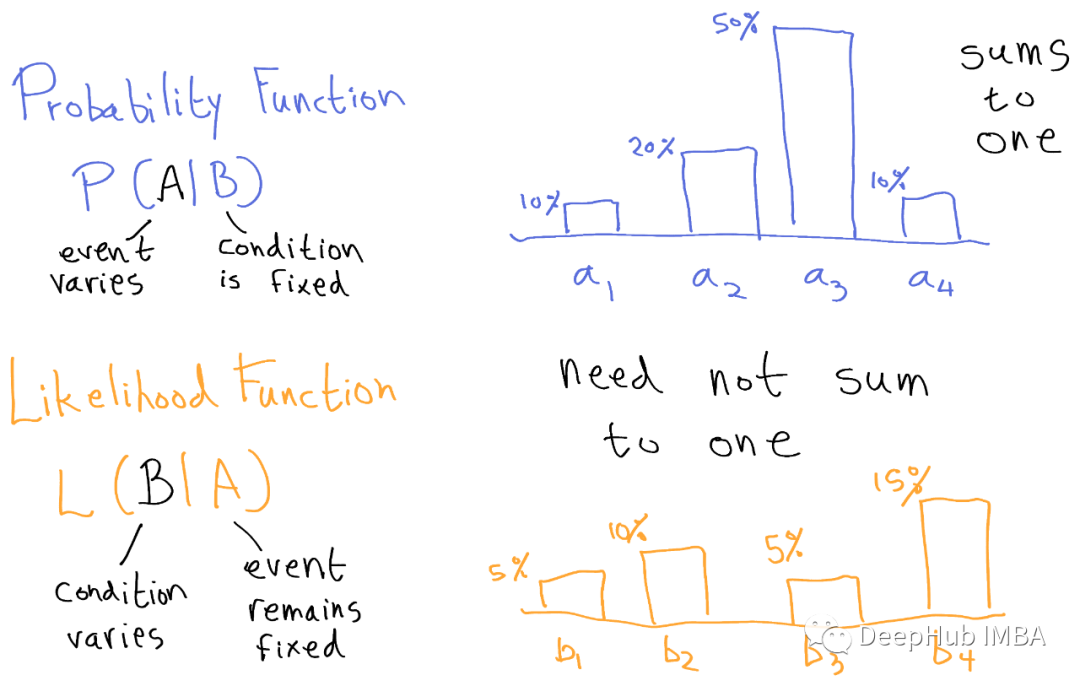
概率与似然
假设在一场棒球比赛中,两队的队长都被召集到场上掷硬币。获胜的队长将根据掷硬币的结果选择先击球还是先投球。
现在,获胜的队长选择先击球的概率是多少?我们现在知道只有两种可能的结果:获胜的队长决定先投球或开始击球。获胜的队有50%的几率会选择先击球。

评论员现在正在讨论获胜队长选择首先在击球的可能性。在实际中这个数字可能不到 50%,因为选择先击球会受球场类型、天气、对方球队等因素的影响。比如说如果比赛前下了大雨,决定先击球的可能性会低至 1%。如果天气条件恰到好处,那么获胜的队选择先击球的可能性可能高达 95%。
所以在计算概率值时,我们相信参数值θ=0.5是正确的。在考虑了所有参数之后,我们假设我们确定参数值 θ=0.5。但是在计算似然时,我们的目标是确定我们是否可以信任该参数。
所以我们可以说概率是基于纯数学的;然而似然是一个有许多参数和条件的函数。
为什么似然不是概率分布?
在抛硬币的情况下,我们可以阐述以下关于潜在结果 x 的情况。
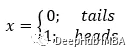
硬币正面朝上的概率是,
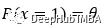
在此基础上,我们可以提出以下关于求硬币正面朝上和反面朝上的概率的问题。
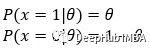
下面的方程可以推广前一组方程。
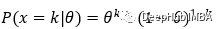
现在,我们可以看到上面的公式适用于k=1和k=0的值。

有了以上的基础,现在要考虑两种不同的情况。
1、概率
假设在抛硬币之前,我们知道参数θ=3/4的值。在此基础上可以说得到正面的概率是P(正面)= θ = 3/4, P(反面)= 1-θ = 1/4。让我们把这些数据画在一个简单的图表上。我们保持参数(θ)不变,并改变数据(x=1或x=0)。
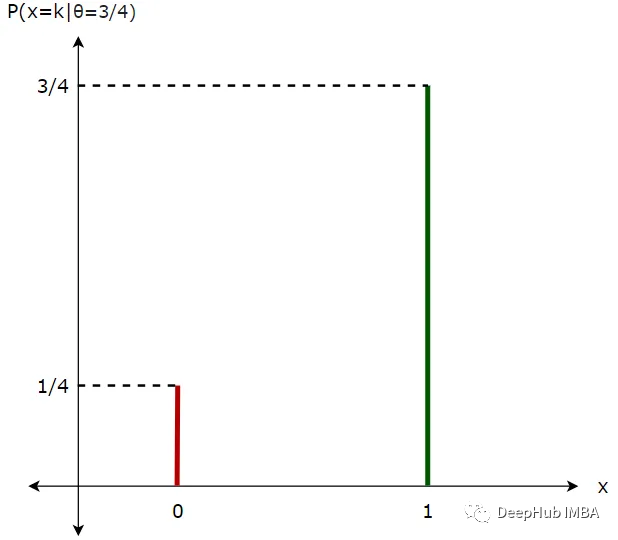
2、似然
现在,假设我们在抛硬币之前不知道正面或反面的概率,而我们有数据的结果, 也就是说我们已经掷过硬币。现在,给定 x=1,找到 θ 的概率是多少。在这种情况下,我们保持数据 (x=1) 不变并更改参数 (θ)。
我们目标是想找到定义这种结果的分布。简而言之,我们想要找到给定 x 的 θ 值。可以将其写成如下的数学格式。
P(x=1 | θ) = L(θ | x=1)
这里需要注意的关键是曲线下的面积是1/2。所以,我们可以说它不是一个有效的概率分布。它被称为似然分布。似然函数不服从概率定律。因此似然函数在[0,1]区间内是无界的。
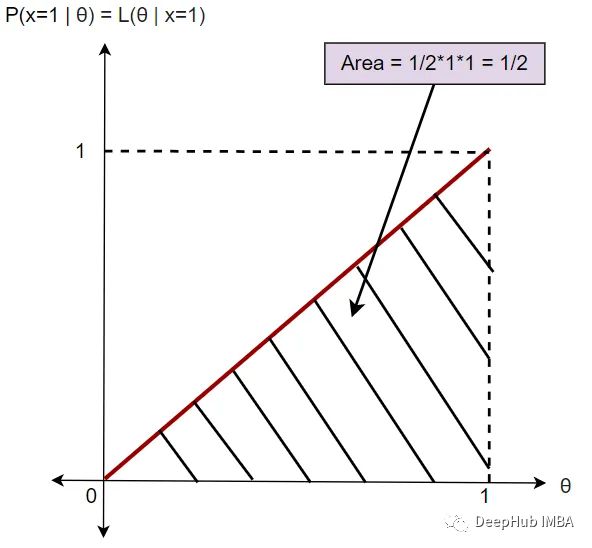
概率和似然之间的关键区别
假设我们从参数化分布 F(X;θ) 中得到一个随机变量 X。在此参数化分布中,θ 是定义分布 F(X;θ) 的参数。随机变量 X=x 的概率为 P(X=x) = F(x;θ),这里的参数 θ 是已知的。
而我们一般情况下会拥有现实世界中的数据 (x),而定义分布 (θ) 的参数是未知的。给定模型 F(X;θ),似然度定义为观测数据 X 随 θ 变化的概率。我们可以将其写为 L(θ) = P(θ; X=x)。这里X 已知,但定义分布 (θ) 的参数未知。定义似然的动机是为了确定分布的参数。
在我们的日常生活中,经常将概率和似然称为同一事物。例如:明天下雨的概率是多少?或者明天下雨的可能性(似然)有多大?但是这些术语在机器学习和统计学中有很大不同。下面的一个例子可以解释概率和似然之间的关键区别。
当我们计算概率结果时,我们假设模型的参数是值得信赖的。但是当我们计算似然时,我们会根据我们观察到的样本数据来确定我们是否可以信任模型中的参数。
抛硬币
如果一枚硬币正面朝上和背面朝上的概率相等,就称其为均匀硬币。换句话说,P(正面)= P(反面)= 1/2。
假设有一枚均匀硬币。我们假设硬币参数值(θ = 0.5)。在寻找概率时,我们假设参数是可信的。也就是说如果我们抛这枚硬币一次,它正面朝上的概率是1/2。现在我们抛硬币100次,发现只有12次是正面朝上的。基于这些证据,我们会说硬币是均匀的可能性非常低。因为如果硬币是均匀的,我们预计它正面朝上的概率是一半,也就是50次。
在上面的例子中,我们可以说,100次硬币正面朝上的概率只有12次,这让我们高度怀疑,因为在给定的条件中,硬币正面朝下的实际概率实际上是p = 0.5。但如果这枚硬币55次正面,我们就可以说这枚硬币很可能是均匀的。
概率问题和统计问题的区别
假设我们还是抛硬币。考虑以下两个场景。
概率问题:
我们假设硬币是均匀的。连续得到两个正面的概率是多少?
它表示给定参数值(P = 0.5),观察数据(序列)的概率是多少。
统计问题:
我们不知道硬币是否公平(我们正在试图确定硬币的公平性)。假设我们抛硬币两次,连续得到两次正面。
问:根据观察到的数据,这枚硬币是均匀的可能性有多大?(p = 0.5)?
这意味着我们在给定数据(sequence = HH)的情况下确定参数的值(P = 0.5)。也就是说“我们的样本在多大程度上支持我们的假设 P = 0.5?”
我们可以将似然定义为参数模型中样本对给定参数值的支持程度的度量。
二项分布的概率和似然
继续抛硬币,让我们考虑一个简单的二项分布的例子。假设我们抛硬币十次,并记录结果。结果是9次正面1次反面。
我们知道硬币是均匀的,即p = 0.5。根据这个信息,我们要算出投掷10次得到9次正面的概率。我们可以用公式

这里0.009765是在p = 0.5的情况下得到x = 9个正面的概率。
一般情况下我们可以这样写:
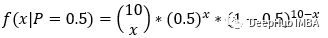
下面,如果我们不确定硬币是否均匀。这意味着我们不知道参数p的值。而我们已经投掷了十次硬币,并得到了投掷结果。结果是9次正面1次反面。基于此,我们可以得出以下结论。
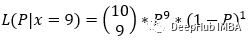
在这里,我们试图根据给定的数据样本(10次抛掷中有9次正面)找到参数P的值。
总结
在机器学习的背景下:
- 概率是指基于模型中参数指定的值,特定结果发生的概率,我们相信参数值是准确的。
- 似然指的是样本对参数模型中给定参数值的支持程度,我们试图根据提供的样本数据确定模型的参数值。
https://avoid.overfit.cn/post/02f9cd888b274752b17a9fc3f1120fbc
作者:Pratik Shukla


![[答疑]经营困难时期谈建模和伪创新-长点心和长点良心](https://img-blog.csdnimg.cn/img_convert/b069adfbb8e4c559e3a1d5585483baf8.png)