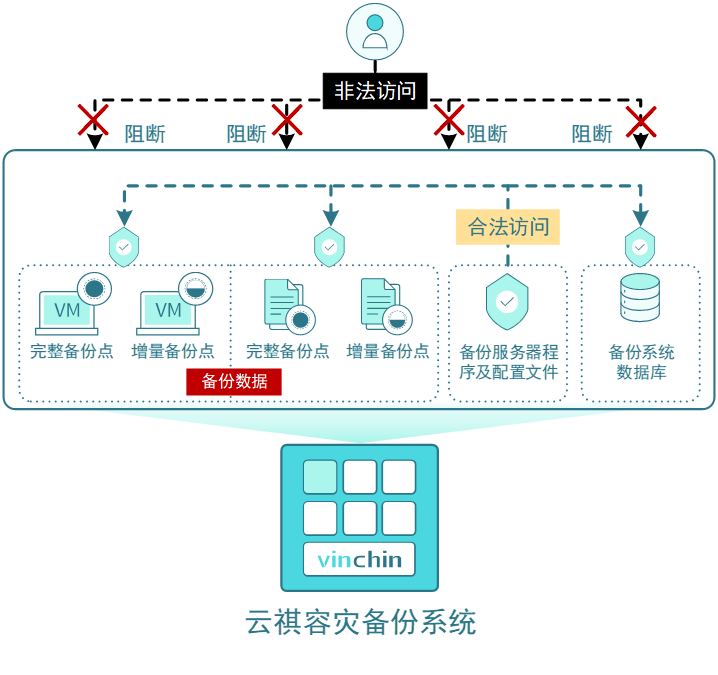
Problem - E - Codeforces

题意：有 n 个怪，生命值为，你有两种操作，一种花费 1 MP减少一个怪的一格血量，可以操作任意次；另一次是花费 x MP，制造一个爆炸，可以不断消灭两侧连续严格递减的数，但只能执行一次（而且是最后一次）；问让消灭所有怪的最小MP花费是多少？

分析：略加思考会想到实际上就是找一个最大的金字塔，两侧都是平原，但实际上并不完全是，因为两侧斜率可以不一样；然后就蒙圈了，显然肯定是要一维枚举塔尖位置，另一维能明显感觉到需要用数据结构维护，为啥呢。显然如果暴力的话就是对每个位置往两边延续，但实际上前面的状态肯定是可以被后面的状态使用的；当时到这里就卡住了；

有三个点：

1. 实际上这种塔尖结构，可以分为两个方向来维护，一个增一个减；

2.发现直接维护不好维护，相对于维护严格递减，不如维护不增【这里就有个小技巧维护】

3.该用什么结构，能维护一个连续区间的最值

这是我之前对维护单调性数据结构的理解还不够深刻，这里再重新理解一下

单调栈由于栈的特性可以维护不连续的单调性，主要 是找到某个位置的左右最值

而单调队列由于是队列先进先出 所以可以维护连续的单调性 至于为啥滑动窗口 单纯有个长度限定而已

得明白两个事：预处理每个数减去坐标之后，只要不减就一定是能满足的，所以对队尾如果比当前的大，那么要减去长度*差值——使满足不减的性质【把山峰不断削平的一个过程】；然后还得处理队头，这里我有个一直想不明白的点：为啥只要处理队头就行了 —— 是因为如果有上一步的合并操作，有可能会使得长度超过他本身的最大长度（本身就是q[hh].val + q[hh].ed），所以要判断if (q[hh].val + q[hh].ed - q[hh].len + 1 <= 0)的条件。（因为如果最新的元素没合并到队头的话，这种肯定不会成立，你想想为什么（因为我们已经预处理过了，只要预处理后严格比你大，那长度就一定合法））

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void slv() {
    int n; cin >> n;
    vector<int> a(n + 1);
    vector<ll> L(n + 1), R(n + 1);
    for(int i = 1 ; i <= n ; i++ ) {
        cin >> a[i];
    }
    struct node{
        int len,val,ed;
    };
    auto cal=[&](vector<ll>& ans){
        vector<ll> pr(n + 2), pr2(n + 2);
        for(int i = 1 ; i <= n ; i++ ) {
            pr[i] = pr[i - 1] + a[i];
        }
        vector<int> a2(n + 1);
        for(int i = 1 ; i <= n ; i++ ) {
            a2[i] = a[i] - i;
            pr2[i] = pr2[i - 1] + a2[i];
        }
        vector<node> q(n + 2);
        int hh = 0, tt = -1;
        ll sm = 0;
        for(int i = 1; i <= n ; i++ ) {
            node cur={1, a2[i], i};
            sm += a2[i];
            while(hh <= tt && q[tt].val >= a2[i]) {
                sm -= 1ll * (q[tt].val - a2[i]) * q[tt].len; //累递过来都是被削平了
                cur.len += q[tt--].len;
            }
            q[++tt] = cur;
            if(hh <= tt && q[hh].val + q[hh].ed - q[hh].len < 0) {
                int len = q[hh].val + q[hh].ed;
                sm -= 1ll * (q[hh].len - len) * q[hh].val;
                q[hh].len = len;
            }//sm其实就是不断削削剩下的部分
            int pre = q[hh].ed - q[hh].len;
            ans[i] += pr[pre] + pr2[i - 1] - pr2[pre] - (sm - a2[i]);
        }
    };

    cal(L);
    auto debug=[&](vector<ll> ve){
        for(int i = 1 ; i <= n ; i++ ) {
            cout << ve[i] << ' ';
        }
        cout << '\n';
    };
//    debug(L);
    reverse(a.begin() + 1, a.end());
    cal(R);
    ll ans = 1e18;
    reverse(a.begin() + 1, a.end());
    for(int i = 1 ; i <= n ; i++ ) {
        ans = min(ans, L[i] + R[n - i + 1] + a[i]);
    }
    cout << ans << '\n';
}
int main() {
    ios::sync_with_stdio(false); cin.tie(0);
    int t; cin >> t;
    while(t--) {
        slv();
    }
}

 参考了知乎cup大佬的代码，自己太菜了搞了半天才搞懂Educational Codeforces Round 143 (Rated for Div. 2) A - F - 知乎