简介

      本章主要讲解一些树的基本概念,二叉树的三种打印方式，二叉查找树和字典树的应用，红黑树的概念。

1.树 (Tree)

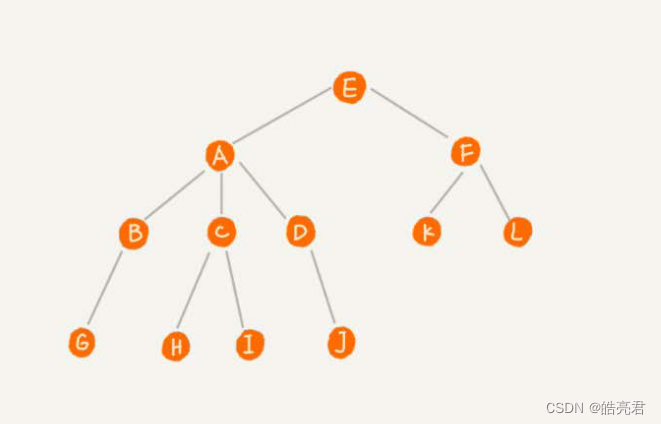
      像这种递归结构数据类型叫做树，例如后台管理系统里菜单存储数据结构就是这种,树的节点包含: 根节点、父节点、子节点、兄弟节点、叶子节点。
      在下面这幅图，E节点是根节点,A节点就是B节点的父节点，B节点是A节点的子节点。B、C、D这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫作根节点，也就是图中的节点E。我们把没有子节点的节点叫作叶子节点或者叶节点，比如图中的G、H、I、J、K、L都是叶子节点。

关于“树”，还有三个比较相似的概念：高度（Height）、深度（Depth）、层（Level）。

• 节点的高度：节点到最底层子节点的最长路径
• 节点的深度：根节点到这个节点所经历的的个数
• 节点的高度：节点的深度+1

如上图节点对应高度、深度、层如下表

节点名称	高度	深度	层
E	3	0	1
A	2	1	2
B	1	2	3
G	0	3	4

      在我们的生活中，“高度”这个概念，其实就是从下往上度量，比如我们要度量第10层楼的高度、第13层楼的高度，起点都是地面。所以，树这种数据结构的高度也是一样，从最底层开始计数，并且计数的起点是0。
      “深度”这个概念在生活中是从上往下度量的，比如水中鱼的深度，是从水平面开始度量的。所以，树这种数据结构的深度也是类似的，从根结点开始度量，并且计数起点也是0。
      “层数”跟深度的计算类似，不过，计数起点是1，也就是说根节点的位于第1层。

2.二叉树（Binary Tree）

2.1.二叉树数据结构

      二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。我画的这几个都是二叉树。以此类推，你可以想象一下四叉树、等长什么样子。

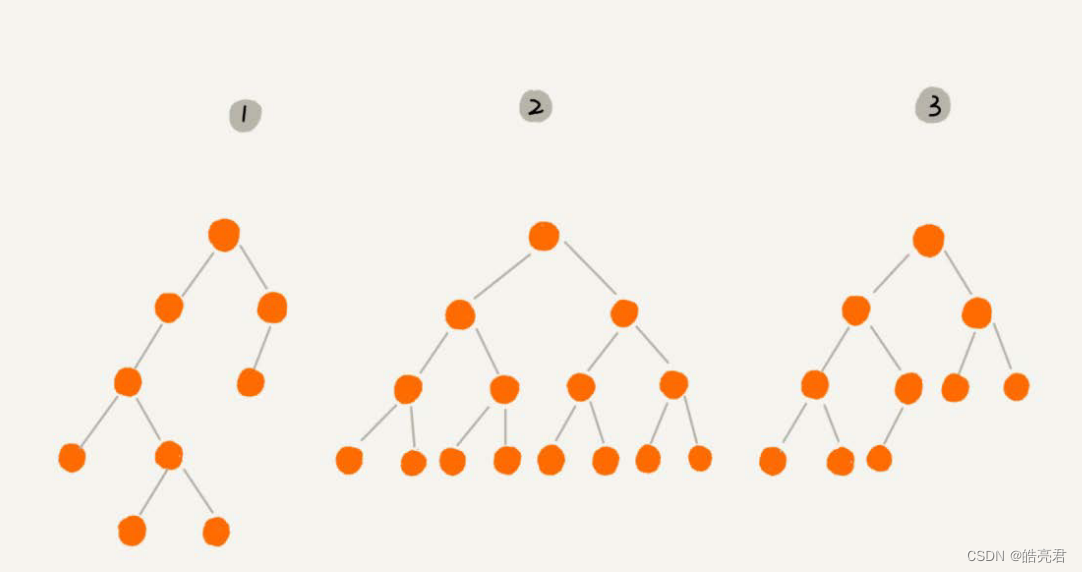
这上图中有两个比较特殊的二叉树，分别是编号2和编号3这两个。

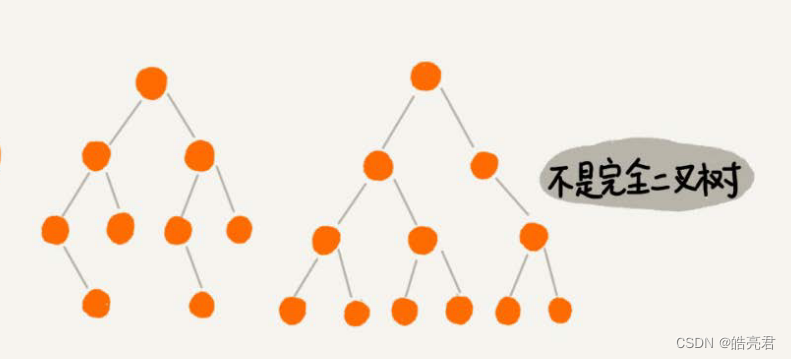
• 编号2的二叉树中，叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。
• 编号3的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。

下图左边的树由于叶子节点靠右部不符合完全二叉树的特性要求，右图因为非叶子节点没有达到最大(2个）所以也不符合。

java定义树节点

@Data
public class TreeNode<T> {
        /*
         * 节点存储的值Val
         */
        private T data;
        /*
         * 子节点左边的数据
         */
        private TreeNode<T> left;
        /*
         * 子节点右边的数据
         */
        private TreeNode<T> right;
		
        public TreeNode(T data) {
            this.data = data;
        }
}

2.2.二叉树的三种遍历方式

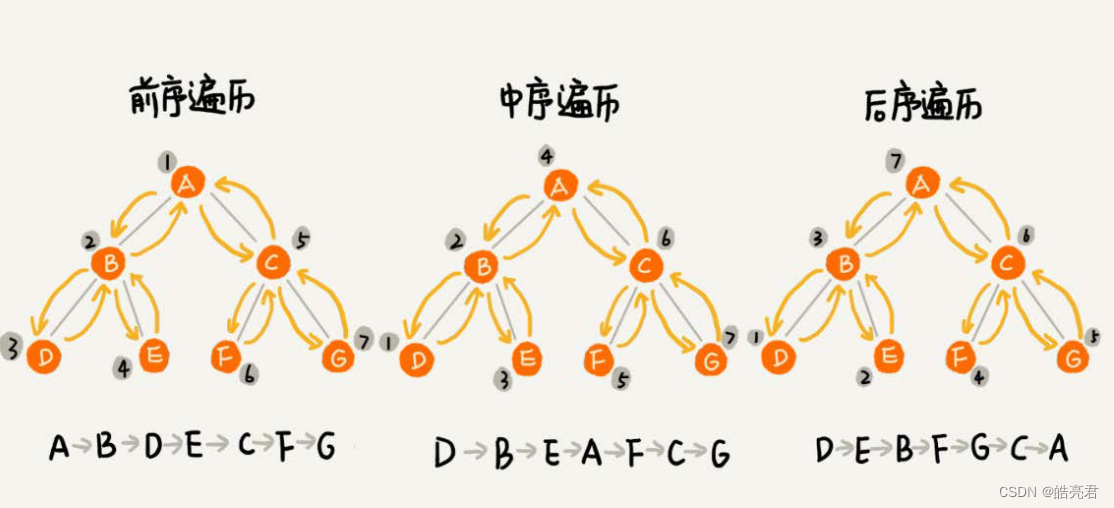
      将所有节点都打印出来的方法有三种，前序遍历、中序遍历和后序遍历。其中，前、中、后序，表示的是节点与它的左右子树节点遍历打印的先后顺序。

• 前序遍历: 对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
• 中序遍历: 对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
• 后序遍历: 对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

前、中、后序遍历的递推公式都写出来。

• 前序遍历的递推公式：preOrderPrint( r ) = print r->preOrderPrint(r->left)->preOrderPrint(r->right)
• 中序遍历的递推公式：inOrderPrint( r ) = inOrderPrint(r->left)->print r->inOrderPrint(r->right)
• 后序遍历的递推公式：postOrderPrint( r ) = postOrderPrint(r->left)->postOrderPrint(r->right)->print r

以下是java实现对二叉树的三种打印实现

    /**
     * 前序遍历 对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树
     * 13 10 9 11 16 14 15
     */
    public static void preOrderPrint(TreeNode root) {
        if (root != null) {
            System.out.print(root.getData() + " ");
            preOrderPrint(root.getLeft());
            preOrderPrint(root.getRight());
        }
    }
    /**
     * 中序遍历 对于树中的任意节点来说，先打印它的左子树，然后再打印它的本身，最后打印它的右子树。
     * 9 10 11 13 14 16 15
     */
    public static void inOrderPrint(TreeNode root) {
        if (root != null) {
            inOrderPrint(root.getLeft());
            System.out.print(root.getData() + " ");
            inOrderPrint(root.getRight());
        }
    }

    /**
     * 后序遍历  对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印它本身。
     * 9 11 10 14 15 16 13 后序打印
     */
    public static void postOrderPrint(TreeNode root) {
        if (root != null) {
            postOrderPrint(root.getLeft());
            postOrderPrint(root.getRight());
            System.out.print(root.getData() + " ");
        }
    }
     	/**
     *        13
     *   10        16
     * 9   11    14   15
     */
    public static void main(String[] args) {
        System.out.println("             13\n" +
                "        10        16\n" +
                "      9   11    14   15");
        TreeNode<Integer> root = new TreeNode<>(13);
        TreeNode<Integer> left = new TreeNode(10);
        TreeNode<Integer> right = new TreeNode(16);
        root.setLeft(left);
        root.setRight(right);

        TreeNode<Integer> left1 = new TreeNode(9);
        TreeNode<Integer> right1 = new TreeNode(11);
        left.setLeft(left1);
        left.setRight(right1);

        TreeNode<Integer> left2 = new TreeNode(14);
        TreeNode<Integer> right2 = new TreeNode(15);
        right.setLeft(left2);
        right.setRight(right2);

        System.out.print("前序遍历:");
        preOrderPrint(root);
        System.out.println();
        System.out.print("中序遍历:");
        inOrderPrint(root);
        System.out.println();
        System.out.print("后续遍历:");
        postOrderPrint(root);
    }

3.二叉查找树(Binary Search Tree)

3.1.二叉查找树的概念和定义

      二叉查找树是二叉树中最常用的一种类型，也叫二叉搜索树。顾名思义，二叉查找树是为了实现快速查找而生的。不过，它不仅仅支持快速查找一个数据，还支持快速插入、删除一个数据。它是怎么做到这些的呢？
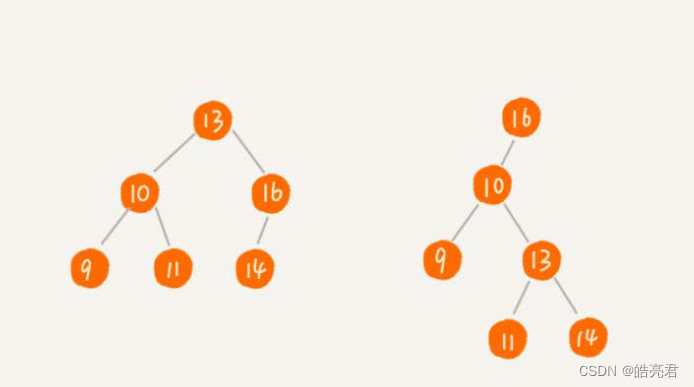
      这些都依赖于二叉查找树的特殊结构。二叉查找树特性要求，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值。 二分查找算法就是通过这种特性在有序的数组实现快速查找某个数字。
从下图两个二叉查找树的例子就应该就清楚了。

      以下代码是Java对二叉查找树的基本功能实现，数据结构和2.1章节的二叉树一样，插入和查找都比较容易理解,只有删除节点涉及到调整数据结构所以会比较复杂。

@Data
public class BinarySearchTree {

    private TreeNode tree;

    public void preOrderedPrint(TreeNode root) {
        if (root != null) {
            System.out.print(root.data + " ");
            preOrderedPrint(root.left);
            preOrderedPrint(root.right);
        }
    }

    /**
     * 查找数据
     *
     * @param data
     * @return 返回node节点
     */
    public TreeNode search(int data) {
        TreeNode p = tree;
        while (p != null) {
            if (data < p.data) {
                p = p.left;
            } else if (data > p.data) {
                p = p.right;
            } else {
                return p;
            }
        }
        return null;
    }

    /**
     * 插入数据
     *
     * @param data
     */
    public void insert(int data) {
        //首次插入初始化树
        if (tree == null) {
            tree = new TreeNode(data);
            return;
        }
        //赋值给临时遍历
        TreeNode p = tree;
        while (p != null) {
            //判断插入的数据是否比根节点数据大，大则往右节点插入
            if (data > p.data) {
                if (p.right == null) {
                    //初始化新节点数据并赋值给当前节点的右索引
                    p.right = new TreeNode(data);
                    return;
                }
                //如果不为空,则遍历子树一直找到合适的位置位置
                p = p.right;
            } else {
                if (p.left == null) {
                    //初始化新节点数据并赋值给当前节点的左索引
                    p.left = new TreeNode(data);
                    return;
                }
                //如果不为空,则遍历子树一直找到合适的位置位置
                p = p.left;
            }
        }
    }


    /**
     * 删除数据
     *
     * @param data
     */
    public void delete(int data) {
        // curNode指向要删除的节点，初始化指向根节点
        TreeNode curTreeNode = tree;
        // parentNode记录的是p的父节点
        TreeNode parentTreeNode = null;

        //查找数据是否存在
        while (curTreeNode != null && curTreeNode.data != data) {
            parentTreeNode = curTreeNode;
            if (data > curTreeNode.data) {
                //如果查找的数据大于当前数据,则往右边查找
                curTreeNode = curTreeNode.right;
            } else {
                //如果查找的数据小于当前数据,则往左边查找
                curTreeNode = curTreeNode.left;
            }
        }

        if (curTreeNode == null) {
            // 没有找到
            return;
        }

        // 要删除的节点有两个子节点
        if (curTreeNode.left != null && curTreeNode.right != null) {
            // 查找右子树中最小节点
            TreeNode minTreeNode = curTreeNode.right;
            // minParent表示minP的父节点
            TreeNode minParent = curTreeNode;
            while (minTreeNode.left != null) {
                //调整节点位置
                minParent = minTreeNode;
                minTreeNode = minTreeNode.left;
            }
            // 将minNode的数据替换到curNode中
            curTreeNode.data = minTreeNode.data;
            // 下面就变成了删除minParent了
            curTreeNode = minTreeNode;
            parentTreeNode = minParent;
        }

        // 删除节点是叶子节点或者仅有一个子节点
        TreeNode child; // p的子节点
        if (curTreeNode.left != null) {
            child = curTreeNode.left;
        } else if (curTreeNode.right != null) {
            child = curTreeNode.right;
        } else {
            child = null;
        }
        if (parentTreeNode == null) {
            // 删除的是根节点
            tree = child;
        } else if (parentTreeNode.left == curTreeNode) {
            parentTreeNode.left = child;
        } else {
            parentTreeNode.right = child;
        }
    }

    @Data
    public class TreeNode {
        /*
         * 节点存储的值Val
         */
        private int data;

        /*
         * 子节点左边的数据
         */
        private TreeNode left;

        /*
         * 子节点右边的数据
         */
        private TreeNode right;

        public TreeNode(int data) {
            this.data = data;
        }

    }

3.2.二分查找算法

      二分查找是一种非常高效的查找算法，高效到什么程度呢？我们来分析一下它的时间复杂度。
我们假设数据大小是n，每次查找后数据都会缩小为原来的一半，也就是会除以2。最坏情况下，直到查找区间被缩小为空，才停止。

      可以看出来，这是一个等比数列。其中n/2k=1时，k的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较，所以，经过了k次区间缩小操作，时
间复杂度就是O(k)。通过n/2k=1，我们可以求得k=log2n，所以时间复杂度就是O(logn)。

由此可见章节3.1的二叉查找树的查询效率是非常高的，时间复杂度和二分查找算法一致。

 /**
     * 使用二分查找数据
     * @param nums 原数据
     * @param find 查找的数字
     */
    public static Integer search(int nums[], int find) {
        //设置标志位，区分是否查找成功
        int index = -1;
        //统计比较次数
        int count = 0;
        //右偏移的数
        int low = 0;
        //中位数
        int mid;
        //范围
        int high = nums.length;
        while (low <= high) {
            count++;
            mid = (low + high) / 2;
            //防止出现没找到这个数出现下标越界
            if (mid > nums.length) {
                break;
            }
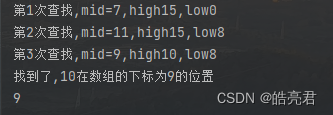
            System.out.println("第" + count + "次查找,mid=" + mid + ",high" + high + ",low" + low);
            if (find == nums[mid]) {
                index = mid;
                System.out.println("找到了," + find + "在数组的第" + mid + "下标");
                break;
            } else if (find > nums[mid]) {
                //如果要找的数大于中位数,在中位数右边,则设置右偏移的值=中位数+1
                low = mid + 1;
            } else {
                //如果要找的数小于中位数,在中位数左边，则设置范围=中位数-1
                high = mid - 1;
            }
        }
        if (index != -1) {
            System.out.println("找到了,下标为" + index);
        } else {
            System.out.println("没有找到这个数" + find);
        }
        return index;
    }

调用示例如下:

    public static void main(String[] args) {
        //需要查找的数据
        int find = 10;
        int[] nums = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15};
        System.out.println(search(nums, find));
    }

基于递归方式的实现二分查找如下

    /**
     * 二分查找 递归实现版本
     */
    public static int dsearch(int[] nums, int find) {
        return dsearch(nums, 0, nums.length - 1, find);
    }

    /**
     * @param nums 数据
     * @param low 右偏移的数
     * @param high 查找的范围
     * @param find 查找的数字
     * @return
     */
    private static int dsearch(int[] nums, int low, int high, int find) {
        if (low > high) {
            //偏移量大于范围终止递归查询
            return -1;
        }
         //计算出中位数   >>1 相当于num除以2 
        int mid = low + ((high - low) >> 1);
        if (nums[mid] == find) {
            return mid;
        } else if (nums[mid] < find) {
            return dsearch(nums, mid + 1, high, find);
        } else {
            return dsearch(nums, low, mid - 1, find);
        }
    }

4.字典树(Trie)

      Trie树，也叫“字典树”。顾名思义，它是一个树形结构。它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。
      举个简单的例子来说明一下。我们有6个字符串，它们分别是：how，hi，her，hello，so，see。我们希望在里面多次查找某个字符串是否存在。如果每次查找，都是拿要查找的字符串跟这6个字符串依次进行字符串匹配，那效率就比较低，有没有更高效的方法呢？

      这个时候，我们就可以先对这6个字符串做一下预处理，组织成Trie树的结构，之后每次查找，都是在Trie树中进行匹配查找。Trie树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。最后构造出来的就是下面这个图中的样子。

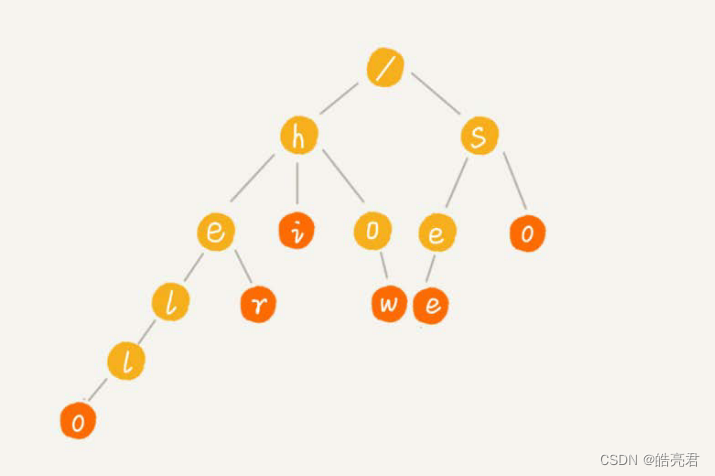
字典树的数据存储过程如下：

像百度查询中输入前缀自动补全的功能就是基于字典树特性实现的。

Java中实现字典树

public class Trie {

    /**
     * 根节点
     */
    private TrieNode root = new TrieNode();

    /**
     * 往Trie树中插入一个字符串
     *
     * @param str 字符串
     */
    public void insert(String str) {
        char[] text = str.toCharArray();
        TrieNode node = root;
        for (int i = 0; i < text.length; ++i) {
            char index = text[i];
            if (!node.map.containsKey(index)) {
                node.map.put(index, new TrieNode());
            }
            node = node.map.get(index);
        }
        node.end = true;
    }

    /**
     * 查找字符
     *
     * @param patternStr 匹配字符
     * @return
     */
    public boolean search(String patternStr) {
        return find(patternStr, false);
    }

    /**
     * 根据前缀查找是否存在
     *
     * @param prefix 匹配字符前缀
     * @return
     */
    public boolean startsWith(String prefix) {
        return find(prefix, true);
    }

    /**
     * 查找字符串是否存在
     *
     * @param patternStr 匹配字符
     * @param prefix     是否前缀匹配
     * @return 结果
     */
    private boolean find(String patternStr, boolean prefix) {
        TrieNode node = root;
        char[] pattern = patternStr.toCharArray();
        for (int i = 0; i < pattern.length; ++i) {
            char index = pattern[i];
            if (!node.map.containsKey(index)) {
                return false;
            }
            node = node.map.get(index);
        }
        if (prefix) {
            return true;
        }
        return node.end;
    }

    /**
     * 单词补齐
     *
     * @param patternStr
     * @return
     */
    public List<String> wordFill(String patternStr) {
        TrieNode node = root;
        char[] pattern = patternStr.toCharArray();
        char index;
        List<String> list = new ArrayList();
        StringBuffer sb = new StringBuffer();

        // 找到字符串末字符在字典树中的位置
        for (int i = 0, j = pattern.length; i < j; i++) {
            index = pattern[i];
            if (node.map.containsKey(index)) {
                sb.append(index);
                node = node.map.get(index);
            } else {
                return null;
            }
        }
        scanFind(node, String.valueOf(sb), list);
        return list;
    }


    /**
     * 子树单词补全
     * @param node   当前节点
     * @param prefix 前缀词
     * @param list   补词后的数据
     */
    private void scanFind(TrieNode node, String prefix, List<String> list) {
        for (Map.Entry<Character, TrieNode> entry : node.map.entrySet()) {
            list.add(prefix + entry.getKey());
            scanFind(entry.getValue(), prefix, list);
        }
    }

    @Data
    public class TrieNode {
        /**
         * 存储字典树
         */
        Map<Character, TrieNode> map;
        /**
         * 是否结尾字符
         */
        boolean end;
        public TrieNode() {
            map = new HashMap<>();
        }
    }

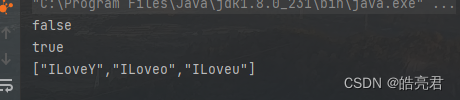
测试字典树的前缀查找、完整查找、单词补全功能

    public static void main(String[] args) {
        Trie tree = new Trie();
        tree.insert("ILove");
        tree.insert("ILoveYou");
        //完整查找
        System.out.println(tree.search("ILoveYo"));
        //前缀查找
        System.out.println(tree.startsWith("ILove"));
        //单词补全
        System.out.println(JSONObject.toJSONString(tree.wordFill("ILove")));
    }

5.红黑树(Red-Black Tree)

      章节3讲的二叉查找树是最常用的一种二叉树，它支持快速插入、删除、查找操作，各个操作的时间复杂度跟树的高度成
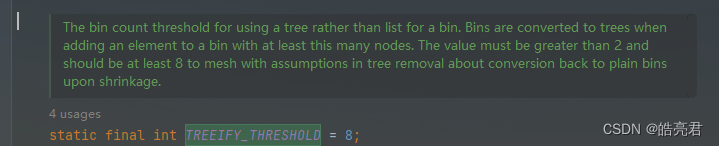
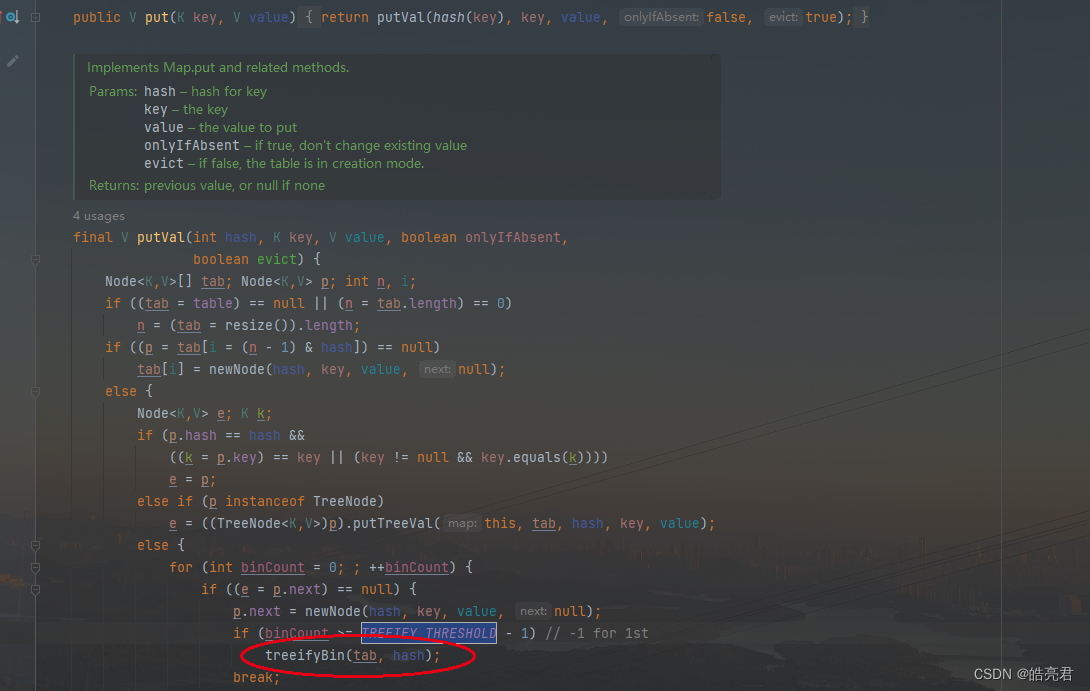
正比，理想情况下，时间复杂度是O(logn)。不过，二叉查找树在频繁的动态更新过程中，可能会出现树的高度远大于log2n的情况，从而导致各个操作的效率下降。极端情况下，二叉树会退化为链表，时间复杂度会退化到O(n)。我上一节说了，要解决这个复杂度退化的问题，我们需要一种平衡二叉查找树，其典型的代表是红黑树,在Jdk1.8里的HashMap里put数据时候出现hash冲突的时候会把数据会存放在链表里,当链表长度大于8的时候会把数据转存储到红黑树里。

什么是“平衡二叉查找树”？
      平衡二叉树的严格定义是这样的：二叉树中任意一个节点的左右子树的高度相差不能大于1。从这个定义来看，完全二叉树、满二叉树其实都是平衡二叉树，但是非完全二叉树也有可能是平衡二叉树。

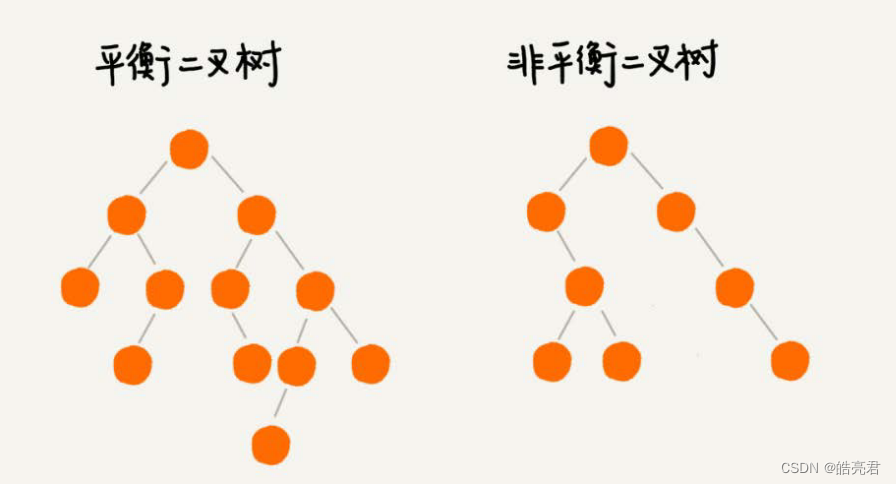
      平衡二叉查找树不仅满足上面平衡二叉树的定义，还满足二叉查找树的特点。最先被发明的平衡二叉查找树是AVL树，它严格符合我刚讲到的平衡二叉查找树的定义，即任何节点的左右子树高度相差不超过1，是一种高度平衡的二叉查找树。但是很多平衡二叉查找树其实并没有严格符合上面的定义（树中任意一个节点的左右子树的高度相差不能大于1），比如此章讲的红黑树，它从根节点到各个叶子节点的最长路径，有可能会比最短路径大一倍。

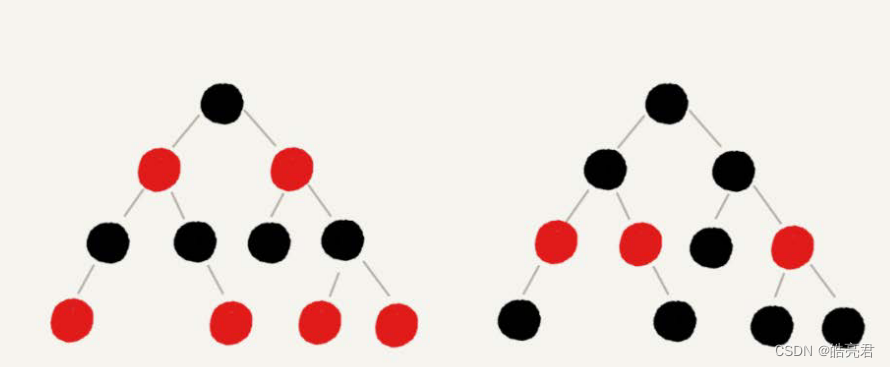
顾名思义，红黑树中的节点，一类被标记为黑色，一类被标记为红色。除此之外，一棵红黑树还需要满足这样几个要求：

• 根节点是黑色的；
• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
• 每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

如下都符合红黑树的定义

Java中HashMap里定义的红黑树数据结构如下,可以看到有一个字段用来标识节点是红色还是黑色。