文章目录
- 蛮力法之排序
- 选择排序
- 冒泡排序
- 实际应用
- 蛮力法之最近对和凸包问题
- 最近对问题
- 凸包问题
蛮力法(brute force),其本质跟咱常说的暴力法是一样的,都是一种简单直接地解决问题的方法,通常直接基于问题的描述和所涉及的概念定义进行求解。
蛮力法之排序
选择排序
选择排序,其本质是将位置与对应的数据大小相匹配,比如:在遍历整个列表时,先找到最小(大)的元素,将其与第一个元素交换;再从第二个元素开始遍历,找到第二小(大)的元素,将其与第二个元素交换;再从第n-1个元素开始遍历,找到第n-1小(大)的元素,将其与第n-1个元素交换。在遍历列表n-1次后,列表就按指定顺序排列完成。此时:
A
1
⩽
A
2
⩽
A
3
⩽
…
…
⩽
A
n
−
1
⩽
A
n
A~1~\leqslant A~2~\leqslant A~3~\leqslant ……\leqslant A~n-1~\leqslant An
A 1 ⩽A 2 ⩽A 3 ⩽……⩽A n−1 ⩽An
其实现代码为:
void selectSort(int*a,int len)
{
for(int i=0;i<len;++i)
{
for(int j=i+1;j<len;++j)
{
if(a[i]>a[j])
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}
案例分析
如果我们使用选择排序对列表 0,2,4,1,9,6,3,8,5,7进行排序,那么其排序过程将会是:

使用DEV跑得到结果:

其时间复杂度为O(n2),空间复杂度为0(n)
)
冒泡排序
冒泡排序,其本质是比较相邻两个元素大小,即,如果 an-1< an ,那么就交换两者位置, 而选择排序是选择相应的元素放置到合适的位置。
其实现代码为:
void bubbleSort(int*a,int len)
{
for(int i=0;i<len-1;++i)
{
for(int j=0;j<len-1-i;++j)
{
if(a[j]>a[j+1])
{
int temp = a[j+1];
a[j+1] = a[j];
a[j] = temp;
}
}
}
}
案例分析
如果我们使用冒泡排序对列表 0,2,4,1,9,6,3,8,5,7进行排序,那么其排序过程将会是:

使用DEV跑得到结果:

与选择排序一样,其时间复杂度为O(n2),空间复杂度为0(n)
实际应用
问题:应用选择排序将序列E,X,A, M,P,L,E按照字母顺序排序。
程序解答
直接将上述的选择排序排序内容从整数变成字符即可,一样的逻辑。
#include <iostream>
using namespace std;
void outPut(char *a,int len)
{
for(int i=0;i<len;i++)
cout<<a[i]<<" ";
cout<<endl;
}
void selectSort(char*a,int len)
{
for(int i=0;i<len-1;++i)
{
for(int j=i+1;j<len;++j)
{
if(a[i]>a[j])
{
char temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}
int main(void)
{
char a[] = {'E','X','A','M','P','L','E'};
cout<<"排序前:";
outPut(a,7);
selectSort(a,7);
cout<<"排序后:";
outPut(a,7);
return 0;
}
蛮力法之最近对和凸包问题
最近对问题
最近对问题描述
最近点对问题要求:在一个包含n个点的集合中,找出距离最近的两个点。这种处理平面或者高维空间的邻近点的问题,在各种计算几何问题当中是最简单的。问题中的点可以代表飞机、邮局这类实体对象,也可以代表数据库记录、统计样本或者 DNA序列等非实体对象。航空交通控制人员可能会对两架最可能发生碰撞的飞机感兴趣。区域邮政管理者可能需要依赖最近对问题的解来寻找地理位置最近的邮局。
解答
使用蛮力法解决最近对问题,一般是采用先将任意两点之间的距离求出,再找到这些距离中的最小值。
例如:
题目
在集合{16,4,23,6,5,94,77}中打印出两数差值最小的两个数;
解析:
由上述最近对问题核心:求两两数值的最小差值,不难有下图中的求解过程:

根据上述的模拟过程,可写出下述程序:
#include <iostream>
#include <math.h>
using namespace std;
void findMinValue(int*a,int len)
{
int minValue,dp[2];
// 遍历数组 求任意两数之差
for(int i=0;i<len-1;i++)
{
for(int j=i+1;j<len;j++)
{
int temp = abs(a[i]-a[j]);
// 比较是否是最小的差
if((i==0&&j==1) || temp < minValue)
{
dp[0] = a[i];
dp[1] = a[j];
minValue = temp;
}
}
}
cout<<"差值最小的两数为:"<<dp[0]<<" "<<dp[1]<<endl;
}
int main(void)
{
int a[] = {16,4,23,61,5,94,77};
findMinValue(a,7);
return 0;
}
使用DEV运行求解有:
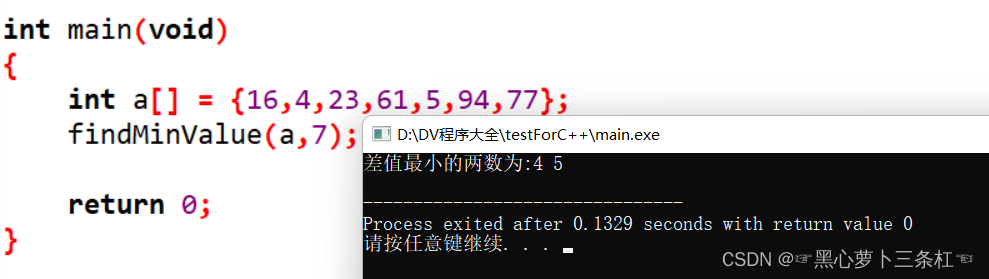
与选择排序类似,该程序的时间复杂度为O(n2),空间复杂度为O(n)。
凸包问题
设p,=(x1, y1), p2=(x2,y2). …, pn=(xn,yn)是平面上n个点构成的集合S,包含集合S中所有点的最小多边形就称为凸包多边形,也就是将最外围所有点连接起来构成的多变形,将其称为凸包多边形。 下图就是一个包含点集的凸包多边形。

例如:
求出二维平面中点 (1,1),(2,1)、(4,1)、(2,2)、(3,2)、(4,2)、(2,3)、(4,3)、(5,3)、(3,4) 所构成的最小凸包。
人为画出凸包多边形有:

分析:
凸包多边形,是由点集最外层点所构成,再结合上图,是不是可以看出当凸边多边形边确定时,其他点都在边的一侧。从数学角度上来说,也就是当凸边多边形边确定时,任意一点到这条边的距离的符号相同(即同为正数,或同为负数,或者为0)。
然后,在将任意两点连接构成一条直线,再判断这条直线是否符合上述凸边多边形边的性质,如果符合该性质就这两点加入到结果集中;否则就继续找其他的直线。
当以点(1,1)为凸包多边形边的一点时,将该点依次连接其他任意点,例如:连接点(2,1),通过点到直线的距离公式,可以算出任意点到该直线都为正数,因此,可以作为凸多边形的一边;而连接点(5,3)时,由于点散落在直线两侧,使用距离公式,可以算出部分点到直线距离为正数,而剩余点到直线的距离为负数,因此,该边不可作为凸多边形的一边。

根据上述的分析,可以写出下述程序:
#include<iostream>
#include<cmath>
#include<vector>
#include<map>
using namespace std;
int check(vector<pair<float, float> >&data,pair<float, float>&target)
{
// 判断数组data中是否已经包含该数值 包含就返回1 否则返回0
for(int i=0;i<data.size();i++)
if(data[i].first==target.first && data[i].second==target.second)
return 1;
return 0;
}
vector<pair<float, float> > convexHull(vector<pair<float,float> > &point){
// 集合点少于2时 可以直接返回
if(point.size() <= 2)
return point;
vector<pair<float, float> > pointPairVec;
//两个循环扫描每个点
for(int i=0; i<point.size()-1; i++){
for(int j=i+1; j<point.size(); j++){
// 求一个一次函数的直线A:ax+by=c (a=y2-y1,b=x2-x1,c=x1y2-y1x2)
float a = point[j].second - point[i].second;
float b = point[i].first - point[j].first;
float c = point[i].first*point[j].second - point[i].second*point[j].first;
//记录直线两边的点
int sign1 = 0, sign2 = 0;
//扫描直线A外的所有的点
for(int k=0; k<point.size(); k++){
if(k==i || k==j)
continue;
else{
// 求点到直线A的距离
float sign = a*point[k].first + b*point[k].second - c;
// 该点在直线上边
if(sign > 0)
sign1++;
// 该点在直线下边
else if(sign < 0)
sign2++;
}
}
// 该点不符合要求 继续查找
if(sign1 > 0 && sign2 > 0)
continue;
// 将符合要求的两点加入结果集
else{
// 将不重复的值加入到结果集
if(!check(pointPairVec,point[i]))
pointPairVec.push_back(point[i]);
if(!check(pointPairVec,point[j]))
pointPairVec.push_back(point[j]);
}
}
}
return pointPairVec;
}
int main(){
// 保存数据集
vector<pair<float, float> > pointsArray(10);
// 生成数据集
pointsArray[0] = pair<float, float>(1,1);
pointsArray[1] = pair<float, float>(2,1);
pointsArray[2] = pair<float, float>(4,1);
pointsArray[3] = pair<float, float>(2,2);
pointsArray[4] = pair<float, float>(3,2);
pointsArray[5] = pair<float, float>(4,2);
pointsArray[6] = pair<float, float>(4,3);
pointsArray[7] = pair<float, float>(2,3);
pointsArray[8] = pair<float, float>(5,3);
pointsArray[9] = pair<float, float>(3,4);
cout<<"源数据:"<<endl;
for(int i=0; i<pointsArray.size(); i++)
cout<<"("<<pointsArray[i].first<<","<<pointsArray[i].second<<")"<<" ";
vector<pair<float, float> > convex = convexHull(pointsArray);
cout<<endl<<"求出能够构成凸包的点:"<<endl;
for(int i=0; i<convex.size(); i++)
cout<<"("<<convex[i].first<<","<<convex[i].second<<")"<<" ";
return 0;
}
DEV跑出结果为:

小编主学嵌入式,算法能力一般,欢迎大家查看小编其他文章,同时也欢迎大家留言或私信交流哈!