时隔两年半（2年4个月），我又回来研究生成技术了。以前学习研究GAN没结果，不管是技术上，还是应用产品上，结果就放弃了，现在基于diffusion的技术又把生成技术带上了一个新的高度。现在自己又来研究学习这方面的东西了。现在看来，以前还是自己自我定位不清晰，想搞研究，搞出研究成果来，自己能力不够，也没人带，搞不了；然后格局不够，对事物曲折变化认识不够，坚持力也不够。现在就还是面向应用进行学习研究了。当时的GAN生成效果还差一截，但是现在的完全能够达到真实效果了，并且技术使用难度也没那么大，应该能做成受欢迎产品级的效果了。

一、基本概念
扩散模型 diffusion
当前主要有四大生成模型：生成对抗模型、变微分自动编码器、流模型以及扩散模型。扩散模型（diffusion models）是当前深度生成模型中新SOTA。
不止于图像生成：
从连续到离散，计算机视觉，语音生成，NLP、波形信号处理、多模态建模、分子图建模、时间序列建模、对抗性净化等都有出色表现。
做研究的话：
其实大部分的研究者都不需要理解扩散模型的数学本质，更需要的是对扩散模型的原理的经验化理解，从而应用到research里面去。

基本数学原理：

它的原理相当复杂，很多数学推导。然后一些具体的东西也不用知道，以俺们的水平，知道了也不能根据原理推导出什么性质，从而帮助做什么提升性工作。要知道其性质，只能直接从经验角度走，以及看网上的资料了。
下面的可以不看吧

视频教程好一点
https://www.bilibili.com/video/BV1r14y1Y7xa/?spm_id_from=333.788.recommend_more_video.9&vd_source=832fdd9b4041ab8d66be70be56266213
diffusion model 最近在图像生成领域大红大紫，如何看待它的风头开始超过 GAN ？ - 路橙LuChengTHU的回答 - 知乎
https://www.zhihu.com/question/536012286/answer/2533146567
从最开始说起，深度学习就是拟合概率函数，通过大量数据学习到大量参数，来拟合这个函数。（现实中很多的智能任务就是在计算一个概率函数？）
一般的深度学习任务，输出维度很低。
比如图片分类，拟合输入数据到输出分类这么一个函数。
注意到这里图片数据是多维的，这是一个多维到一维的函数，单值函数。
而生成模型则是反过来，输入低维数据，得到高维数据，这个可以叫做结构化学习？

这里生成对象可以是不同的东西，图片矩阵，文字序列都可以，需要具体控制。
输入的低维数据就代表要生成对象的特征，比如狗，黄色的狗到图片，狗为主题到一篇文章。然后生成过程就交给深度学习模型去拟合了。

https://zhuanlan.zhihu.com/p/563543020
https://zhuanlan.zhihu.com/p/34998569 这篇文章最好
我们看回生成模型到底是个啥。我们拿到一批样本（比如图片，称为 X ），想要学到它的分布p(X)，这样就能同时学到没被采样到的数据了，用这个分布 p(X) 就能随意采样，然后获得生成结果。(这里怎么采样？高维空间上X值在某些点概率很大，某些点概率很低，但是这样采样没有意义。）。于是这里引入一个隐变量Z，就是前面说得特征，高维数据在低维空间的流形。不妨假设Z服从正态分布，然后根据Z来生成X。Z和X具有一个条件概率关系p(X|Z) ，然后利用条件概率和全概率公式计算得到p(X),从而学习到X的分布，同时得到特征隐变量z和x的关系。

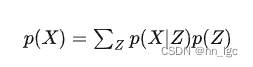
在这里插入图片描述

这个条件概率p(X|Z) 就描述了一个由 Z 来生成 X的模型，约等于生成器G。

于是，从VAE和GAN，他们都是从隐变量 Z（对象特征）生成目标数据X，但是实现上有所不同。
更准确地讲，它们是假设了Z服从某些常见的分布（比如正态分布或均匀分布），训练一个模型G，这个模型将原来的概率分布映射到训练集的概率分布，即X‘=g(Z)。也就是说，它们的目的都是进行分布之间的变换。

最后当然是希望促使模型得到的分布 X’ 和目标分布 X尽量接近。这个就是生成模型的难题，如何判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

那现在假设Z服从标准的正态分布，那么我就可以从中采样得到若干个 Z1,Z2,…,Zn，然后对它做变换得到 X̂1=g(Z1),X̂2=g(Z2),…,X̂n=g(Zn)，我们怎么判断这个通过 G 构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？

有读者说不是有 KL 散度吗？当然不行，因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式。

GAN的做法就是直接把这个判断方法也用神经网络学习过来就行，边生成边训练。但是仍然有问题，后面讲到。

而VAE 则使用了一个精致迂回的技巧。
VAE的核心：
其实，在整个 VAE 模型中，我们并没有去使用 p(Z)（先验分布）是正态分布的假设，我们用的是假设 P(X|Z) （后验分布）是正态分布。
具体来说，给定一个真实样本 Xk，我们假设存在一个专属于 Xk 的分布 p(Z|Xk)（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。（我理解这里Z是大Z，代表集合，就是每个z值到x_k的概率形成的分布吧。）

为什么要强调“专属”呢？因为我们后面要训练一个生成器 X=g(Z)，希望能够把从分布 p(Z|Xk) 采样出来的一个 Zk 还原为 Xk。
如果假设 p(Z) 是正态分布，然后从 p(Z) 中采样一个 Z，那么我们怎么知道这个 Z 对应于哪个真实的 X 呢？现在 p(Z|Xk) 专属于 Xk，我们有理由说从这个分布采样出来的 Z 应该要还原到Xk 中去。

那我怎么找出专属于 Xk 的正态分布 p(Z|Xk) 的均值和方差呢？找出均值方差就知道分布了，好像并没有什么直接的思路。
那好吧，我就用神经网络来拟合出来。这就是神经网络时代的哲学：难算的我们都用神经网络来拟合。

于是我们构建两个神经网络 $μk=f1(Xk)，logσ^2=f2(Xk)来算它们了。我们选择拟合 logσ^2 而不是直接拟合 σ^2，是因为 σ^2 总是非负的，需要加激活函数处理，而拟合 logσ^2$ 不需要加激活函数，因为它可正可负。

这里没太明白，反正就是构造神经网络，把均值方差算出来了。

到这里，我能知道专属于 Xk 的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个 Zk 出来，然后经过一个生成器得到 X̂k=g(Zk)。

现在我们可以放心地最小化 D(X̂k,Xk)^2，因为 Zk 是从专属 Xk 的分布中采样出来的，这个生成器应该要把开始的 Xk 还原回来。于是可以画出 VAE 的示意图：
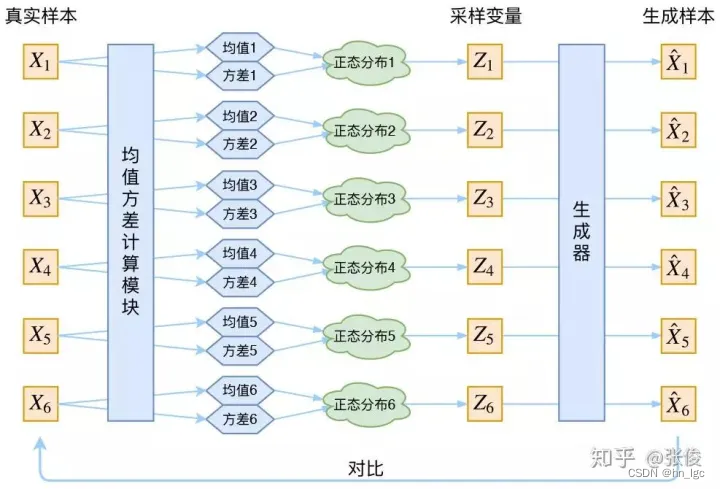
在这里插入图片描述
VAE 的本质是什么
它本质上就是在我们常规的自编码器的基础上，对 encoder 的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果 decoder 能够对噪声有鲁棒性；而那个额外的 KL loss（目的是让均值为 0，方差为 1），事实上就是相当于对 encoder 的一个正则项，希望 encoder 出来的东西均有零均值。

模型结构

https://zhuanlan.zhihu.com/p/525106459
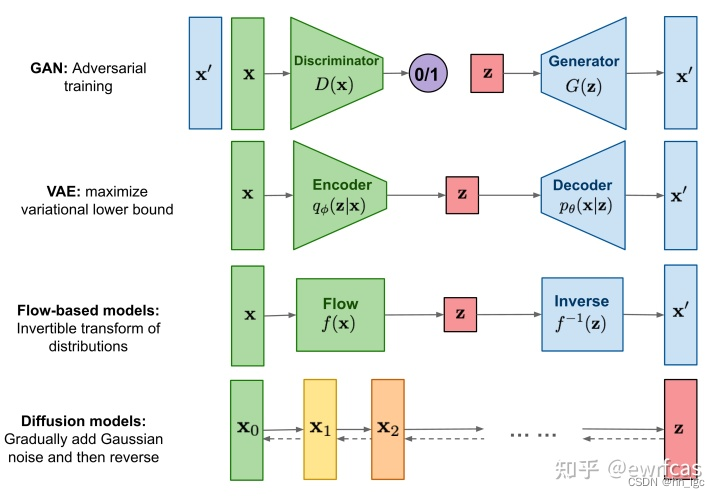
在这里插入图片描述
diffusion model和其他模型最大的区别是它的latent code(z)和原图是同尺寸大小的（正常情况）。一句话概括diffusion model，即存在一系列高斯噪声（ T 轮），将输入图片 x0 变为纯高斯噪声 xt 。而我们的模型则负责将 xt 复原回图片 x0 。这个和GAN像，只是噪声维度不同。

Diffusion前向过程
所谓前向过程，即往图片上加噪声的过程。虽然这个步骤无法做到图片生成，但是这是理解diffusion model以及构建训练样本GT至关重要的一步。
在这里插入图片描述
前向过程介绍结束前，需要讲述一下diffusion在实现和推导过程中要用到的两个重要特性。

特性1：重参数（reparameterization trick）
重参数技巧在很多工作（gumbel softmax, VAE）中有所引用。如果我们要从某个分布中随机采样(高斯分布)一个样本，这个过程是无法反传梯度的。而这个通过高斯噪声采样得到的过程在diffusion中到处都是，因此我们需要通过重参数技巧来使得他可微。
在这里插入图片描述

Diffusion逆向（推断）过程

如果说前向过程(forward)是加噪的过程，那么逆向过程(reverse)就是diffusion的去噪推断过程。

步骤总结：每个时间步通过 xt 和t来预测高斯噪声，然后计算得到均值和方差，再计算一个中间量xxx，最后重参数得到xt-1

训练过程简记

在这里插入图片描述

采样过程

测试（采样）如图右边 Algorithm 2 Sampling部分：

从标准高斯分布采样一个噪声 xT∼N(0,I) ；
从时间步 T 开始正向扩散迭代到时间步 1；
如果时间步不为1，则从标准高斯分布采样一个噪声 z∼N(0,I) ，否则 z=0；
根据高斯分布计算每个时间步 t 的噪声图；

缺点总结

作者：路橙LuChengTHU
链接：https://www.zhihu.com/question/536012286/answer/2533146567
来源：知乎

变分后验分布的表达能力与计算代价的权衡一直是VAE领域的核心痛点。
GAN还需要额外训练判别器，这导致训练很困难；
normalizing flow需要模型是可逆函数，不能随便用一个图像分类or分割领域的SOTA神经网络，这也导致模型表达能力受限。

Diffusion model最初提出是2015年的这篇Deep Unsupervised Learning using Nonequilibrium Thermodynamics，这篇文章写作上跟目前diffusion model非常不一样，而且也没有做work，不建议新手读。真正把diffusion model首次做work的工作是2020年提出的DDPM，其中有许多实现上的细节。抛开这些实现细节，站在2022年回看，我们可以揣测出2015年原作者提出这种模型的初衷。以下内容是我个人的理解。

总而言之，从理论角度来看，diffusion model的成功在于我们训练的模型只需要“模仿”一个简单的前向过程对应的逆向过程，而不需要像其它模型那样“黑盒”地搜索模型。并且，这个逆向过程的每一小步都非常简单，只需要用一个简单的高斯分布来拟合。这为diffusion model的优化带来了诸多便利，这也是它empirical performance非常好的原因之一。

扩散模型主要包括前向过程和后向过程：
前向过程(扩散过程)不断往输入数据中加噪声（标准高斯分布），加噪声其实是构建标签的过程，时间步趋近于正无穷最后变成纯噪声。
后向过程是去噪、不断复原的过程，也是生成目标的过程。

diffusion特点

在图像数据中，目前只有UNET这种网络结构（跨越连接）是work的，别的都不work（可以说是“完全不work”）。
确实目前diffusion model对于低维表征还没有很solid的研究工作，这也是我感兴趣的方向，说不定哪天就想出来了[笑哭][笑哭]
我们最新的研究提出了一个叫DPM-Solver的加速采样算法，证明了DDIM是diffusion ODE的一阶ODE solver，并且提出了二阶、三阶solver，可以做到10步采样质量很不错，20步几乎收敛。不是指噪声过程步数。

diffusion优点：

Diffusion model最大的优势是训练简单。
预测噪声”，其实就是用一个二范数来训练。Diffusion model借助了图像分割领域的UNet，训练loss稳定，模型效果非常也好。相比于GAN需要和判别器对抗训练或者VAE需要变分后验，diffusion model的loss真的是太简单了。
究其本质，其实就是我在1中提到的，diffusion model只需要“模仿”一个非常简单的前向过程对应的逆过程即可。
目前的训练技术让diffusion model直接跨越了GAN领域调模型的阶段，而是直接可以用来做下游任务。

diffusion模型缺点：

23.2
推理速度慢，因为噪声到图片的过程需要生成很多步，每次都运行一遍神经网络，就慢了。
训练速度极其消耗资源，要么慢，要么贵。
相对于GAN，GAN 能更灵活处理不同任务，应用层面部署比较容易，需要的资源小。Diffusion model 相对不太灵活，缺少良好的 latent space 性质。

发展方向:
我相信diffusion model的加速采样肯定会在不久的将来彻底被解决，从而让diffusion model占据深度生成模型的主导。
作者：路橙LuChengTHU
链接：https://www.zhihu.com/question/536012286/answer/2533146567

stable diffusion

资料来源
https://www.ithome.com/0/668/981.htm

https://zhuanlan.zhihu.com/p/583124756
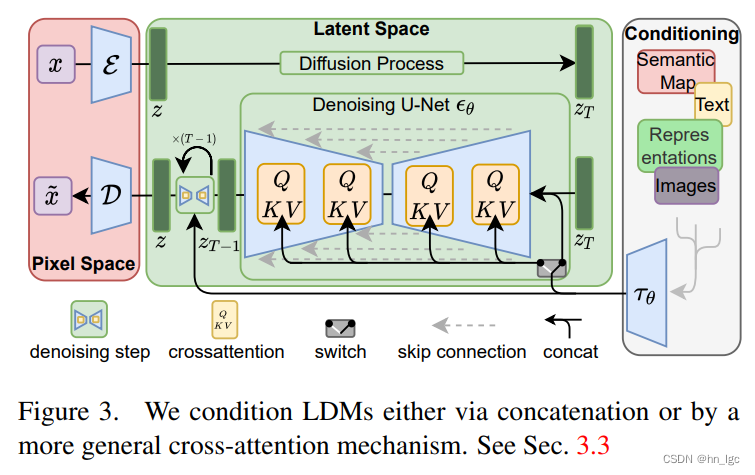
在这里插入图片描述

Stable Diffusion基于Latent Diffusion Models。它是Latent Diffusion Models的一个具体实现，具体来说，它特指这样的一个模型架构设置：自动编码器下采样因子为8，UNet大小为860M。这里看到，sd也是扩散模型的一个小标志，这个后面肯定会有更好的模型出来的吧。
特点：

论文提出一种在潜在表示空间（latent space）上进行diffusion过程的方法，从而能够大大减少计算复杂度，同时也能达到十分不错的图片生成效果。
相比于其它空间压缩方法（如），论文提出的方法可以生成更细致的图像，并且在高分辨率图片生成任务（如风景图生成，百万像素图像）上表现得也很好。
论文将该模型在**无条件图片生成****（unconditional image synthesis）, 图片修复（inpainting）,图片超分（super-resolution）任务上进行了实验，都取得了不错的效果。
论文还提出了cross-attention的方法来实现多模态训练，使得条件图片生成任务也可以实现。论文中提到的条件图片生成任务包括类别条件图片生成（class-condition）, 文图生成（text-to-image）, 布局条件图片生成（layout-to-image）。这也为日后Stable Diffusion的开发奠定了基础。

模型结构

Latent Diffusion Models整体框架如图，首先需要训练好一个自编码模型（AutoEncoder，包括一个编码器和一个解码器）。这样一来，我们就可以利用编码器对图片进行压缩，然后在潜在表示空间上做diffusion操作，最后我们再用解码器恢复到原始像素空间即可，论文将这个方法称之为感知压缩（Perceptual Compression）。个人认为这种将高维特征压缩到低维，然后在低维空间上进行操作的方法具有普适性，可以很容易推广到文本、音频、视频等领域。

在潜在表示空间上做diffusion操作其主要过程和标准的扩散模型没有太大的区别，所用到的扩散模型的具体实现为 time-conditional UNet。但是有一个重要的地方是论文为diffusion操作引入了条件机制（Conditioning Mechanisms），通过cross-attention的方式来实现多模态训练，使得条件图片生成任务也可以实现。
图片感知压缩（Perceptual Image Compression）
感知压缩本质上是一个tradeoff（折中，意思是不是啥创新）。

感知压缩主要利用一个预训练的自编码模型，该模型能够学习到一个在感知上等同于图像空间的潜在表示空间。这种方法的一个优势是只需要训练一个通用的自编码模型，就可以用于不同的扩散模型的训练，在不同的任务上使用。这样一来，感知压缩的方法除了应用在标准的无条件图片生成外，也可以十分方便的拓展到各种图像到图像（inpainting，super-resolution）和文本到图像（text-to-image）任务上。

在第一阶段训练自编码器时，为了避免潜在表示空间出现高度的异化，作者使用了两种正则化方法，一种是KL-reg，另一种是VQ-reg，因此在官方发布的一阶段预训练模型中，会看到KL和VQ两种实现。在Stable Diffusion中主要采用AutoencoderKL这种实现。
在这里插入图片描述

条件机制

除了无条件图片生成外，我们也可以进行条件图片生成，这主要是通过拓展得到一个条件时序去噪自编码器（conditional denoising autoencoder）来实现的，这样一来我们就可通过来控制图片合成的过程。具体来说，论文通过在UNet主干网络上增加cross-attention机制来实现。为了能够从多个不同的模态预处理，论文引入了一个领域专用编码器（domain specific encoder），它用来将多模态数据映射为同一种中间表示 ，这样我们就可以很方便的引入各种形态的条件（文本、类别、layout等等）。最终模型就可以通过一个cross-attention层映射将控制信息融入到UNet的中间层，cross-attention层的实现如下：
其中是UNet的一个中间表征。相应的目标函数可以写成如下形式：
条件图片生成，这主要是通过拓展得到一个条件时序去噪自编码器（conditional denoising autoencoder）来实现的。
在这里插入图片描述
论文设计了大量的对比实验，并分别对感知压缩权衡（下采样因子）、LDM生成效果对比进行了分析验证。并且还在其他任务上进行了实验，包括Super-Resolution、Inpainting、layout-condition在内的多种图片生成等任务，这说明说明LDMs中的学习到的潜在表示空间确实具备很强的分布拟合能力，能够够适配各种下游任务。