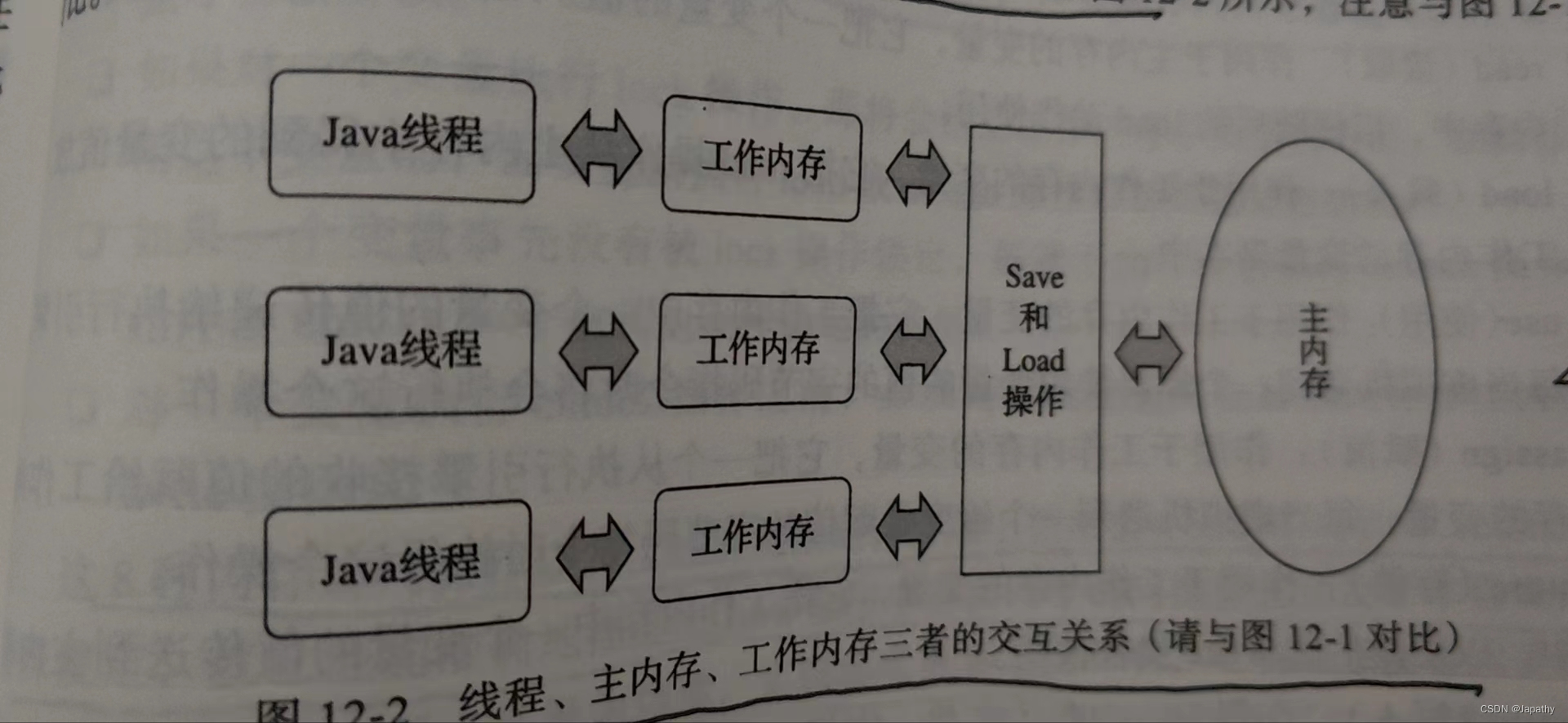
你肯定知道递归，大概也知道尾递归。可是为什么要在递归中分出尾递归这样一个类？尾递归的本质又是什么？许多人未必清楚。

递归原是Lisp语言提出的概念，后来被许多语言借鉴。递归指自我重复的结构，在编程语言中体现为函数的自我调用。递归在算法中有着非常重要的地位，在函数式编程中，递归是最基本的结构，没有循环，只有递归；而在命令式语言中，人人都知道要避免使用递归，因为深度递归会耗尽栈空间。

尾递归是递归中比较特殊的一种情况，经过优化的尾递归不会吞吃栈空间，而是使用固定大小的栈空间，如同循环一样。网上许多对于尾递归的解释是“在函数末尾调用自身”其实是错误的。在函数末尾调用自身不一定是尾递归，但尾递归一定是在末尾调用自身，在末尾调用自身只是尾递归的充分不必要条件。要解释清楚尾递归的本质，还要中函数调用说起。

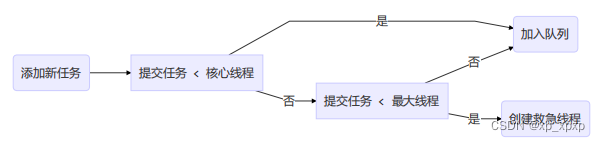
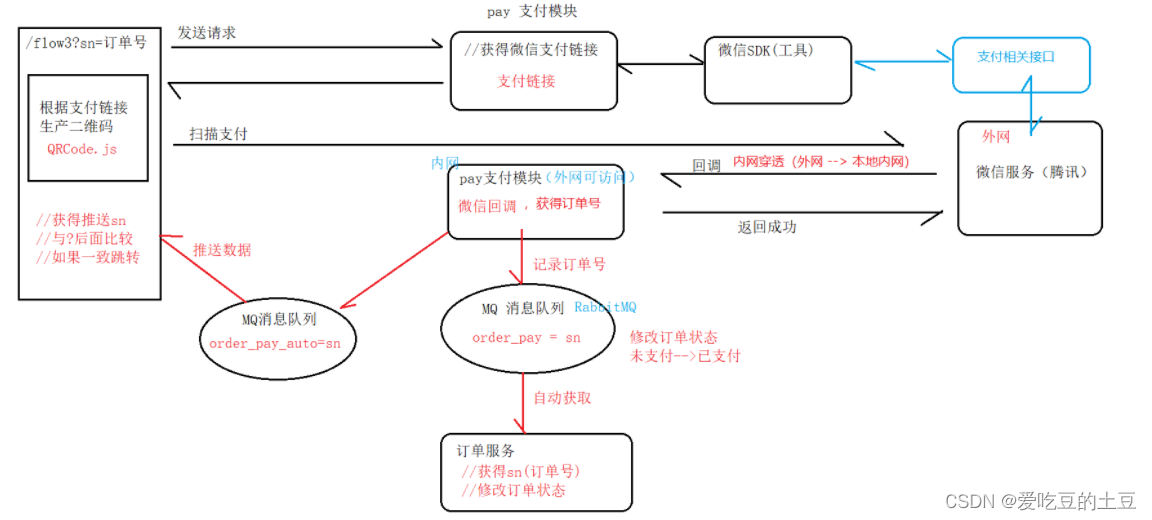
静态的函数只是一堆二进制指令，函数要想运行还需要栈。栈用来存储函数的参数和局部变量(有时包括返回值)，一个函数在运行时其参数和局部变量等占据的空间称为栈帧，如下图所示。

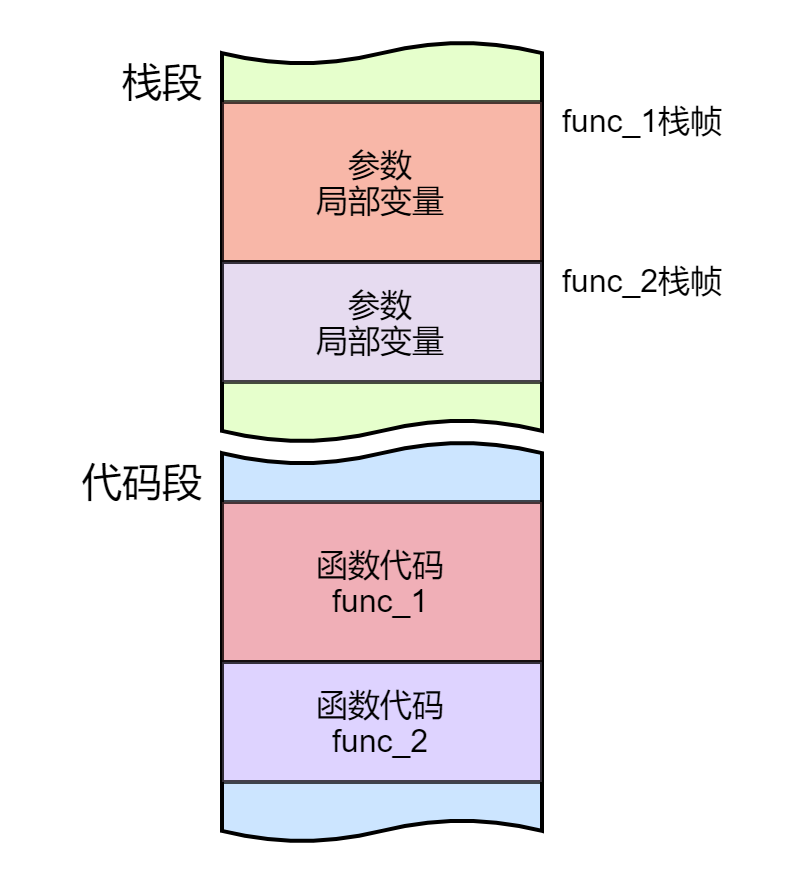
栈帧是一个函数一次运行的快照，是函数的内部状态。也就是说，函数每被调用一次，就会在栈段留下一个栈帧，即便是调用自身也会产生一个新的栈帧。如果想复用栈帧，函数就不能有内部状态，或者说它的状态不会再将来被使用。这才是尾递归的精髓，也只有这样的递归可以被优化，复用之前的栈帧，避免栈空间耗尽。如果只是把尾递归理解为在函数末尾调用自身是片面的。

首先来看下面这个列表求和的例子。

func sumSlice1(s []int) int {
  if len(s) == 0 {
    return 0
  }
  if len(s) == 1 {
    return s[0]
  }
  return s[0] + sumSlice1(s[1:])
}

func sumSlice2(s []int, tmp int) int {
  if len(s) == 0 {
    return tmp
  }
  return sumSlice2(s[1:], tmp+s[0])
}

上例中虽然sumSlice1也是在末尾调用自身，但是它不能进行尾递归优化，因为栈帧需要保存s[0]这个状态。而sumSlice2没有内部状态，可以进行尾递归优化。

还有一个典中典的递归例子是求斐波拉契数列的第n项，如下：

func Fibolacci1(n int) int {
  if n < 2 {
    return n
  }
  return Fibolacci1(n-1) + Fibolacci1(n-2)
}

func Fibolacci2(n, a, b int) int {
  if n == 0 {
    return a
  }
  return Fibolacci2(n-1, b, a+b)
}

Fibolacci1看似没有内部状态，但其实Fibolacci1(n-1)本身就是一个需要存储的状态，我们可以改写如下：

func Fibolacci1(n int) int {
  if n < 2 {
    return n
  }
  a := Fibolacci1(n-1)
  b := Fibolacci1(n-2)
  return a + b
}

这样就能明显看出它不是尾递归了。Fibolacci2没有内部状态，是可以做尾递归优化的版本。

说到状态，我们知道编程语言有两大阵营：函数式编程和命令式编程。前者努力消除状态，后者依赖于状态。所以一般只有函数式编程语言的编译器会去做尾递归优化，然而并不是所有的递归都是天然的尾递归，许多时候需要我们手动消除状态，方式就是把局部变量(状态)变成参数，我称之为状态参数化。这也是函数式编程常用的手段。

再多思考一点，如果将函数调用看作一条时间线，先执行的函数是过去，被调用的函数是未来，也就是过去需要用到将来的结果，这显然是不可能的，至少目前我们的物理学还是因果的。既然无法把将来带回到过去，那么就只能把过去带去未来，方法就是把它记录下来。记忆是人类大脑一项重要的功能，我们也是通过记忆把过去的信息带到未来。

注意，尾递归优化需要编译器的支持，我们在这里讨论的是尾递归的本质以及如何把编译器不能优化的递归改写成可以优化的递归。虽然我们的例子都是用Go写的，但是目前Go编译器是不支持尾递归优化的，想体验尾递归优化可以试试Erlang。