链接1

• 数理统计中的统计推断问题主要有两大类：参数估计问题和假设检验问题
• 参数估计问题
  • 所指参数一般为分布中所含的未知参数、未知参数的函数、分布中的各种特征数
  • 参数估计问题就是根据样本对以上各种未知参数做出估计
    • 一般提法：设有一个总体$X$，总体的分布函数为$F(X;\theta )$，其中$\theta$是未知参数。
    • $X_1,X_2,\cdots ,X_n$是总体$X$的一个样本
    • 现根据该样本对参数$\theta$作出估计，或估计$\theta$的某个已知函数$g(\theta )$
• 假设检验问题

一、假设检验是干啥的

• 假设检验，是用来判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法
• 显著性检验是假设检验中最常用的一种方法，也是一种最基本的统计推断形式（文章最后）
  • 其基本原理是先对总体的特征做出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受做出推断。常用的假设检验方法有Z检验、t检验、卡方检验、F检验等

二、假设检验基本原理/思想

• 核心是小概率原理和反证法
• 小概率思想：小概率事件在一次实验中基本上不会发生
• 对于你想证明的一个观点，若不能直接证明，可以先假设这个观点是错的，再通过推理发现矛盾，反证原本结论是正确的
• 具体到假设检验中，是先提出零假设$H_0$和备择假设$H_1$（你想证明的），通过统计方法计算样本统计量，如果样本观察值导致了小概率事件的发生，就应拒绝原假设
• 概率小到什么程度才能算作“小概率事件”？
  • 显然，“小概率事件”的概率越小，否定原假设H0就越有说服力，常记这个概率值为α(0<α<1)，称为检验的显著性水平。对于不同的问题，检验的显著性水平α不一定相同，一般认为，事件发生的概率小于0.1、0.05或0.01等，即“小概率事件”

三、假设检验步骤

1.提出零假设与备择假设

• 分析问题，确定问题，提出假设
• 假设检验分为双侧检验和单侧检验。简单分辨就是，双侧检验是比较不相等，单侧检验是比大或比小
  • 双侧检验：$$H_0:\mu ={\mu }_0,H_1:\mu \ne {\mu }_0$$
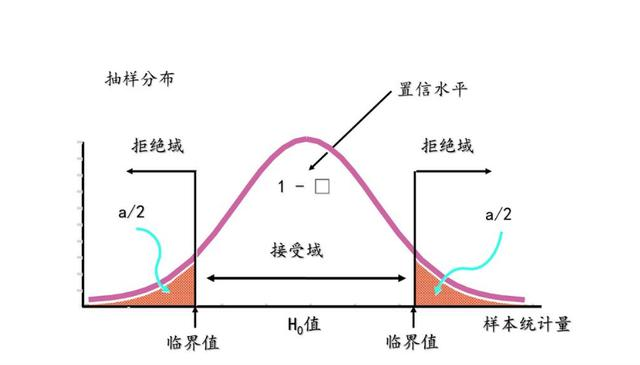
  • 如果检验的目的是检验抽样的样本统计量与假设参数的差是否过大（无论正方向，还是负方向），我们都会把风险分摊到左右两侧。比如显著性水平为5%，则概率曲线的左右两侧各占2.5%，也就是95%的置信区间。
    • 比如：小学生中，男女生的身高是否存在性别差异
  • 单侧检验：$$H_0:\mu ={\mu }_0,H_1:\mu >{\mu }_0$$ $$H_0:\mu \ge {\mu }_0,H_1:\mu <{\mu }_0$$
  • 如果检验的目的只是注重验证是否偏高，或者偏低，也就是说只注重验证单一方向，我们就检验单侧。比如显著性水平为5%，概率曲线只需要关注某一侧占5%即可，即90%的置信区间。
    • 比如：小学生中，男生的平均身高是否大于女生

2.给定显著性水平$\alpha$和样本容量$n$
3.根据问题的特点，提出拒绝域的形式，确定检验统计量
4.由$P(拒绝H_0|H_0为真)=\alpha$，求出拒绝域的具体表达式
5.对总体进行抽样，根据样本值是否落在拒绝域内，做出接受/拒绝$H_0$的判断

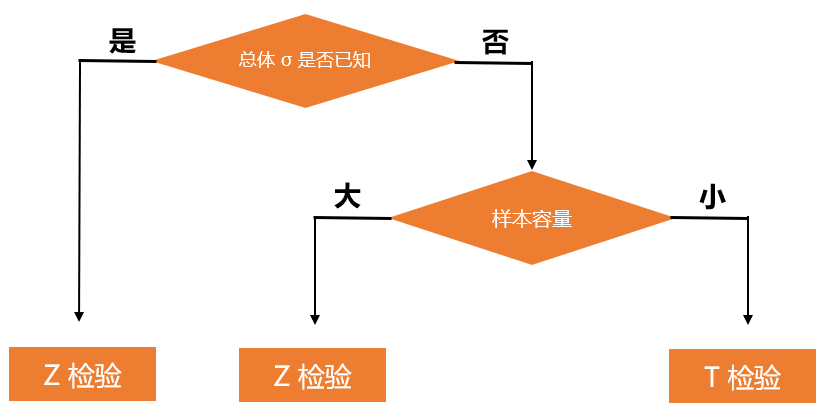
显著性检验(significance test)

统计显著性和置信度

• 任何理论（或认识）都没法保证其关于现实的推测是100%正确的，这归因于理论永远都只是对现实世界真相的大致概括和特征提取。
• 理论只能无限趋近于真实，但无法达到真实。人类用的仅仅是越来越接近真相的理论而已。
• 所以对于任何说法，都有一个可信度问题。
• 而通过对于现实的重复测试，我们将能够了解某说法究竟有多可信，不同的说法之间是存在着可信度的差异的。
• 这就像是盲人摸象之后，每个盲人说出的有关大象外形的可信度是有差别的，而且只要让盲人们多摸几次，他们对大象长相的描述会越来越接近真实。
• 了解不同观点的可信度，是统计的目的之一。
• 统计中所谓的’显著性’就是可信度的一种指标。
• 具有统计显著性的结果反映的是经过严格的测试得到的结果达到了一定可信度一专业术语叫’置信度’（又叫“置信水平”），它表明我们在多大程度上相信结论不会因随机因素而发生偏差。
• 更具体地说，置信度是我们所持理论预测出来的结果在指定区间出现的可能性。
• 显著性跟置信度的内涵异曲同工，但它们的表述方法刚好相反，且在应用中描述方式略有差异：
  • 对于置信度一般我们会说’…实验结果落在某个置信区间的可能性可以达到多高…'（这个可能性越大置信度就越高)
  • 而对于显著性我们会说’.…我们的理论假设被否定的可能性小于多少，我们的假设就可以被称为显著或者极显著…'（这个可能性越小显著性越高）
  • 显著性水平就是变量落在置信区间以外的可能性
  • 也就是说，置信度通常是正面描述（拒伪的），而目通常需要与一个置信区间关联起来。而显著性则是反面描述（拒真的），而且通常需要与一个预设的判断门槛值联系起来。
  • 如果显著性水平是$\alpha$，那么置信度就是$1-\alpha$
  • 

补充：第一类错误和第二类错误

• 第一类错误：原假设为真，却惨遭拒绝，记这一事件发生的概率为$\alpha$
• 第二类错误：原假设为假，确被你接受了，这一事件发生概率为$\beta$

p值是啥

• 说了那么多，所以p值是啥呢

• p值是假设$H_0$成立的概率

• 一般，想要证明什么，零假设就要设它的反面，基于反证法证明本来想证明的东西

• 只要证明$H_0$发生是一个小概率事件：若$p<\alpha$，则这个测试具有统计学显著性

• 如果置信区间不包含零假设的值，则检验结果具有统计显著性

• 一般选取的$\alpha =0.05$