1、图的概念
G=(V,E)
图G由节点集合V=V(G)和边集合E=E(G)组成,其中V为非空有限集合。
集合V中的节点(node)用红色标出,通过集合E中黑色的边(edge)连接。

G的边:E中的每个顶点对(u,v)称为G的边
边的端点:用e表示集合E中的一个顶点对e=(u, v),称u,v为边e的端点
邻接顶点:称u和v是邻接的顶点
关联:一条边的端点称为与这条边关联
邻接的边:若两条不同的边与一个公共的端点关联,称这两条边是邻接的
多重边:若联结两个顶点有不止一条边,这些边称为多重边
环:顶点重合为一点的边称为环
简单图 :没有环也没有多重边的图称为简单图
有限图:一个图如果它的顶点集合与边集合都有限,称为有限图
空图:没有边的图称为空图
标定图:给每一个定点和每一条边指定一个符号,则称这样的图为标定图
完全图:完全图是一个简单的无向图,其中每对不同的顶点之间都有一条边相连
二分图:若图G的顶点集合能分为两个子集V和U,使每一条边有一个端点在V中另一个端点在U中,则称此图为二分图(或二部图)记作G(V,U,E)
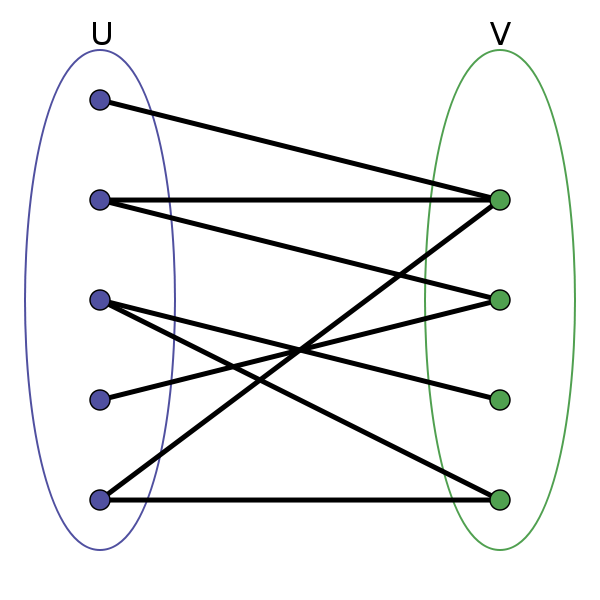
完全二分图 :若V的每个顶点与U的每个顶点都关联,称为完全二分图
补图:一个图G的补图
G
ˉ
\bar{G}
Gˉ也是以V(G)为顶点集的一个图,但是两个顶点在
G
ˉ
\bar{G}
Gˉ中邻接当且仅当它们在G中不邻接。下图b为a的补图。是完全图去除G的边集后得到的图。
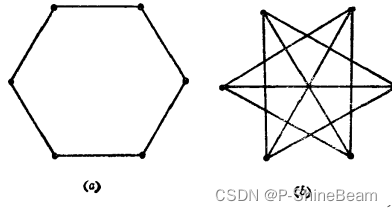
子图:所有顶点和边都属于图G的图称为G的子图
生成子图:含有G的所有顶点的子图称为G的生成子图
导出子图:设图G = (V, E),令S⊂V,使得S是G的任意顶点子集。则G的导出子图G(S)中,其顶点集为S,边集为G的边集E中两个顶点均属于S的边的集合。
2、顶点的度
图G中和一个顶点 v i v_{i} vi关联的边的数目叫做顶点 v i v_{i} vi的度,记作 d e g ( v i ) deg (v_{i}) deg(vi)
定理 1:设G是一个(p, q)图,那么G的各个顶点度的和是边数的二倍:
∑
v
i
∈
V
(
G
)
d
e
g
(
v
i
)
=
2
q
\sum_{v_{i}\in V(G) }^{} deg (v_{i}) = 2q
vi∈V(G)∑deg(vi)=2q
推论 1:在任何一个图G中,度为奇数的顶点的数目是偶数。
在一个(p, q)图中,对每个顶点v均有
0
≤
d
e
g
(
v
)
≤
p
−
1
0\le deg (v) \le p-1
0≤deg(v)≤p−1
孤立点:若 deg (v) = 0,则称v是孤立点
悬挂点:若 deg (v) = 1,称v是一个悬挂点
正则的图:若图G的所有顶点的度均相等,则称G为正则的
r度正则的图:顶点的度均为r的正则图称为r度正则图
出度:指出节点的边数量
入度:指向节点的边数量
定理 2:所有节点入度和等于所有节点出度和
定理3 :n个节点的无向完全图 边数为n(n-1)/2
3、图的连通性
通路
通路:给定图G=(V, E)中的节点和边相继交错出现的序列:
Γ
=
v
0
e
1
v
1
e
2
v
2
.
.
.
e
k
v
k
\Gamma = v_{0} e_{1} v_{1} e_{2} v_{2} ... e_{k} v_{k}
Γ=v0e1v1e2v2...ekvk称
Γ
\Gamma
Γ为节点
v
0
v_{0}
v0到节点
v
0
v_{0}
v0的通路。(其中边
e
i
e_{i}
ei的两端点是
v
i
−
1
v_{i-1}
vi−1和
v
i
v_{i}
vi,有向图时
v
i
−
1
v_{i-1}
vi−1与
v
i
v_{i}
vi分别是
e
i
e_{i}
ei的始点和终点)
通路的端点:
v
0
v_{0}
v0和
v
k
v_{k}
vk分别称为此通路的始点和终点,统称为通路的端点。
通路的长度: 通路中边的数目称为此通路的长度
回路:当
v
0
v_{0}
v0 =
v
k
v_{k}
vk时,此通路称为回路
简单通路:若通路中的所有边互不相同,称此通路为简单通路(也叫做轨迹trail)
简单回路:若回路中的所有边互不相同,称此回路为简单回路
基本通路:通路中所有节点互不相同,所有边也互不相同的通路(也叫做路径path)
基本回路:回路中除
v
0
v_{0}
v0 =
v
k
v_{k}
vk以外所有节点互不相同,所有边也互不相同的回路
通路长度:一条通路上所有边的权的和称为该通路的长度
图的直径:是指连接任意两个节点的所有最短通路中最长的通路长度
连通图
连通:在无向图 G 中,若从顶点i到顶点j有路径相连(当然从j到i也一定有路径)则称i和j是连通的;如果 G 是有向图,那么连接i和j的路径中所有的边都必须同向。
连通图:如果图中任意两点都是连通的,那么图被称作连通图。
强连通图:如果有向图图中任意两点都是连通的,并且双向都有路径,那么这个有向图图被称作强连通图
连通分量:无向图G的极大连通子图称为G的连通分量( Connected Component)。任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。
环路:回路与回路的边的不重并,称为环路
定理3.1:闭链是环路
定理3.2:环路中每个顶点的度均为偶数
定理:连通(p, q)图G关于生成树T的基本回路组做成G的一个基底,且环路空间的维数是q-p+1。由于基本回路组不是唯一的,环路空间的基底也不是唯一的
推论:连通的(p, q)图的环路空间中元素的个数是
2
q
−
p
+
1
2^{q-p+1}
2q−p+1(包括空图)
4、图的运算
设
G
1
G_{1}
G1和
G
2
G_{2}
G2是没有孤立点的图
G
1
G_{1}
G1和
G
2
G_{2}
G2的 并:由
G
1
G_{1}
G1和
G
2
G_{2}
G2中所有边组成图,记作
G
1
∪
G
2
G_{1} \cup G_{2}
G1∪G2
G
1
G_{1}
G1和
G
2
G_{2}
G2的 交:由
G
1
G_{1}
G1和
G
2
G_{2}
G2的公共边组成的图,记作
G
1
∩
G
2
G_{1} \cap G_{2}
G1∩G2
G
1
G_{1}
G1与
G
2
G_{2}
G2的 差:在
G
1
G_{1}
G1中去掉
G
2
G_{2}
G2的边所得到的图,记作
G
1
−
G
2
G_{1} - G_{2}
G1−G2
G
1
G_{1}
G1和
G
2
G_{2}
G2的 环和:在
G
1
G_{1}
G1和
G
2
G_{2}
G2的并中去掉
G
1
G_{1}
G1和
G
2
G_{2}
G2的交得到的图,记作
G
1
⊕
G
2
G_{1}\oplus G_{2}
G1⊕G2
5、树的概念
树:一个连通的无回路的图称为树。
定理5.1:在树中任意两个顶点均由唯一的通路联结
定理5.2:设T是一个(p, q)图,若T是一棵树,则q = p-1
定理5.3:设T是一棵树,若在T的任何两个不临近的顶点联一条边e,则T+e恰有一条回路
定理5.4:如果图G的任意两个顶点由唯一的通路联结,那么G是一棵树
定理5.5:设G是一个(p, q)图,如果G是连通的,且q=p-1,则G是一棵树
定理5.6:设G是一个(p, q)图,如果G无回路且q=p-1,则G是一棵树
割边(桥):去掉图的一条边后,剩下的图的支比原图多(暨图不再连通)
割点:在无向图中删除某顶点后图不再连通,则这个顶点就是这个图的割点
不可分图:连通的没有割点的图称为不可分图
定理5.7:当且仅当G的一条边e不包含在G的回路中时,e才是割边
定理5.8:当且仅当某连通图的每条边均为割边时,该连通图才是一棵树
定理5.9:当且仅当在G中存在与v不同的两个顶点u和w使v在每一条(u, w)通路上v才是割点
定理5.10:设v是树T的一个顶点,则当且仅当degv>1时,v才是割点
定理5.11:每个连通图G至少有两个顶点不是割点
推理5.1:每棵树至少有两个度为1的顶点,且树中最长通路的起点和终点的度均为1
定理5.12:不可分图的任一边至少在一个回路中
6、图的矩阵表示
(1)关联矩阵
完全关联矩阵:
设G是一个(p,q)图,令
a
i
j
=
{
1
,
若边
j
与顶点
i
关联
0
,
否则
a_{ij} = \left\{\begin{matrix} 1,& 若边j与顶点i关联\\ 0,& 否则 \end{matrix}\right.
aij={1,0,若边j与顶点i关联否则
则称由元素
a
i
j
a_{ij}
aij(i=1,…,p,j=1,…,q)构成的p
×
\times
×q矩阵为图G的完全关联矩阵
定理6.1:设G是连通的(p, q)图,那么G的完全关联矩阵的秩是p-1
推论6.1:完全关联矩阵的秩等于它所表示的图的秩
定理6.2:G为连通的(p, q)图,当且仅当G的完全关联矩阵的秩为p-1
大子阵:p
×
\times
×q矩阵的阶为min{p, q}的方阵,称为p
×
\times
×q矩阵的一个大子阵
大行列式:大子阵定义的行列式称为大行列式
定理6.3:设G是一个连通的(p, q)图。G的关联矩阵的一个大子阵是非奇异的当且仅当与这个大子阵的列相对应的边组成G的一颗生成树
(2)回路矩阵
完全回路矩阵:
设G是一个(p,q)图,令
b
i
j
=
{
1
,
若边
j
在环路
i
中
0
,
否则
b_{ij} = \left\{\begin{matrix} 1,& 若边j在环路i中\\ 0,& 否则 \end{matrix}\right.
bij={1,0,若边j在环路i中否则
则称由元素
b
i
j
b_{ij}
bij(i=1,…,
2
q
−
p
+
1
2^{q-p+1}
2q−p+1,j=1,…,q)构成的
2
q
−
p
+
1
2^{q-p+1}
2q−p+1
×
\times
×q矩阵为图G的完全回路矩阵
定理6.4:连通的(p, q)图G的完全回路矩阵的秩等于q-p+1
定理6.5:连通的(p, q)图G的关联矩阵A和完全回路矩阵B满足
A
B
T
AB^{T}
ABT = 0,
B
A
T
BA^{T}
BAT = 0
推论6.2:设B是图G的回路矩阵,则
A
B
T
AB^{T}
ABT = 0,
B
A
T
BA^{T}
BAT = 0
(3)割集矩阵
完全割集矩阵:
设G是一个(p,q)图,令
q
i
j
=
{
1
,
若边
j
在断集
i
中
0
,
否则
q_{ij} = \left\{\begin{matrix} 1,& 若边j在断集i中\\ 0,& 否则 \end{matrix}\right.
qij={1,0,若边j在断集i中否则
则称由元素
q
i
j
q_{ij}
qij(i=1,…,
2
p
−
1
2^{p-1}
2p−1-1,j=1,…,q)构成的
(
2
p
−
1
−
1
)
(2^{p-1}-1)
(2p−1−1)
×
\times
×q矩阵为图G的完全回路矩阵
(4)邻接矩阵
邻接矩阵:
一个图G=(V, X)由V中每两个点间的邻接关系唯一决定,这种关系可以用一个矩阵来表示。设V={
v
1
,
.
.
.
v
p
v_{1},...v_{p}
v1,...vp},p阶方阵A(G) =(
a
i
j
a_{ij}
aij)称为G的邻接矩阵:
若
a
i
j
=
{
1
,
v
i
邻接于
v
j
0
,
v
i
不邻接于
v
j
或
i
=
j
a_{ij} = \left\{\begin{matrix} 1,& v_{i}邻接于v_{j}\\ 0,& v_{i}不邻接于v_{j}或i=j \end{matrix}\right.
aij={1,0,vi邻接于vjvi不邻接于vj或i=j
(5)拉普拉斯矩阵
给定一个有n个顶点的图G,它的拉普拉斯矩阵L=
(
l
i
,
j
)
n
,
n
(l_{i,j})_{n,n}
(li,j)n,n定义为:
L
=
D
−
A
L=D-A
L=D−A其中D为图的度矩阵,A为图的邻接矩阵。
7、图的存储
(1)邻接矩阵
图的邻接矩阵表示法(Adjacency Matrix):也称作数组表示法。
采用两个数组来表示图: 一个是用于存储顶点信息的一维数组;另一个是用于存储图中顶点之间关联关系的二维数组,这个关联关系数组被称为邻接矩阵。
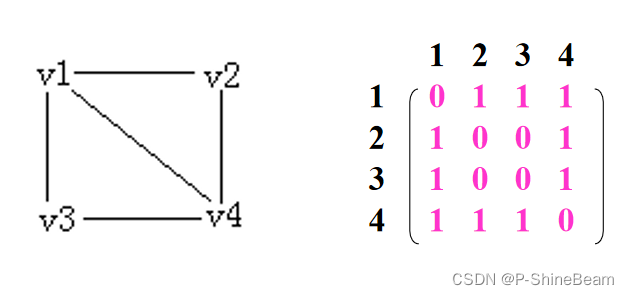
- 在图中各顶点的序号确定后,图的邻接矩阵是唯一确定的
- 邻接矩阵可采用压缩存储
- 适于进行边或弧的删除和插入操作
- 不易于进行顶点的插入删除操作
- 对于稀疏图会造成存储空间的浪费
(2)邻接表
邻接表表示法(Adjacency List):实际上是图的一种链式存储结构。
基本思想是只存有关联的信息,对于图中存在的边信息则存储,而不相邻接的顶点则不保留信息。在邻接表中,对图中的每个顶点建立一个带头结点的边链表。每个边链表的头结点又构成一个表头结点表。一个n个顶点的图的邻接表表示由表头结点表与边链表两部分构成:
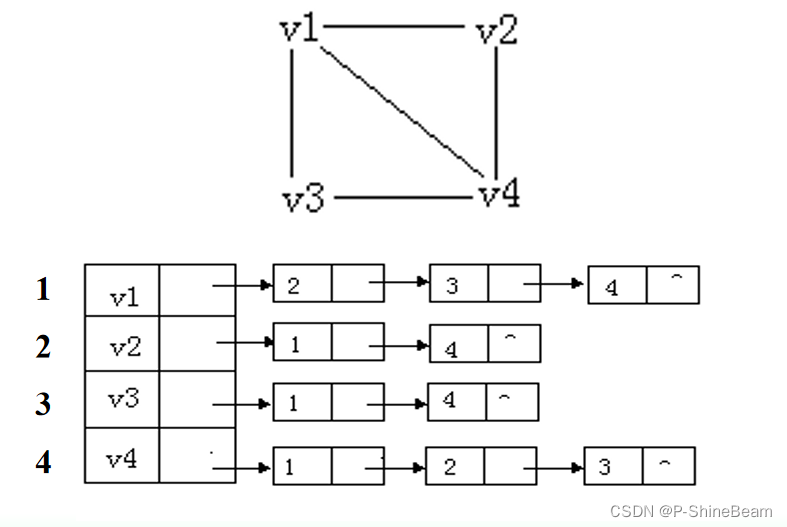
特点:
- 图的邻接表表示不唯一的,它与边结点的次序有关
- 对于顶点多边少的图采用邻接表存储节省空间
- 容易找到任一顶点的第一个邻接点和下一个邻接点
- 无向图的邻接表中第i个顶点的度为第i个链表中结点的个数
- 有向图的邻接表中第i个链表的结点的个数是第i个顶点的出度;而第i个顶点的入度需遍历整个链表,采用逆邻接表,建立一个以vi顶点为头的弧的表
- 无向图的边数等于邻接表中边结点数的一半,有向图的弧数等于邻接表中边结点数
(3)十字链表
邻接表表示有向图时,每个结点对应的边表表示结点的出度信息,无法表示入度信息。
可以采用逆邻接矩阵的方式表示出度信息但不能表示入度信息。因此,考虑将邻接表与逆邻接表结合同时表示有向图的出入度信息,得到十字链表的表示方式
(4)邻接多重表
邻接表表示无向图时边链表会存在大量边信息的冗余,因为邻接表中每条边用两个结点表示的。为了降低冗余,邻接多重表的边链表改用一个边结点表示边来降低冗余。
8、图的常见算法
(1) 寻路和图搜索算法
-
寻路算法:寻找两个节点之间的最短路径。最短路径计算的是一对节点之间的最短的加权(如果图有加权的话)路径。常用算法有:Dijkstra 算法等
-
搜索算法:根据图的相邻情况或深度来探索图,这可用于信息检索;常用算法有:宽度优先搜索(BFS)、深度优先搜索(DFS)
(2) 社群检测
- 社群检测:根据给定的质量指标将节点划分为多个分组,常用算法有Girvan Newman 算法、Louvain 方法、分层聚类算法等
(3) 中心度算法
中心度(Centrality)衡量的是节点的重要程度。但这并非一个明晰的定义。常用算法有PageRank 算法等
参考资料
1、图论【王朝瑞编著】
2、图论与图学习
3、图论基础






![[Android Studio]Android 数据存储--SQLite数据库存储](https://img-blog.csdnimg.cn/24b696d76d374a9992017e1625389592.gif)