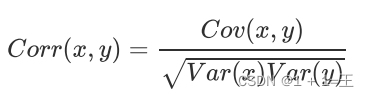文章目录
- 向量与矩阵
- 标量、向量、矩阵、张量
- 向量范数和矩阵的范数
- 导数和偏导数
- 特征值和特征向量
- 概率分布
- 伯努利分布
- 正态分布(高斯分布)
- 指数分布
- 期望、⽅差、协⽅差、相关系数
- 期望
- 方差
- 协⽅差
- 相关系数
向量与矩阵
标量、向量、矩阵、张量
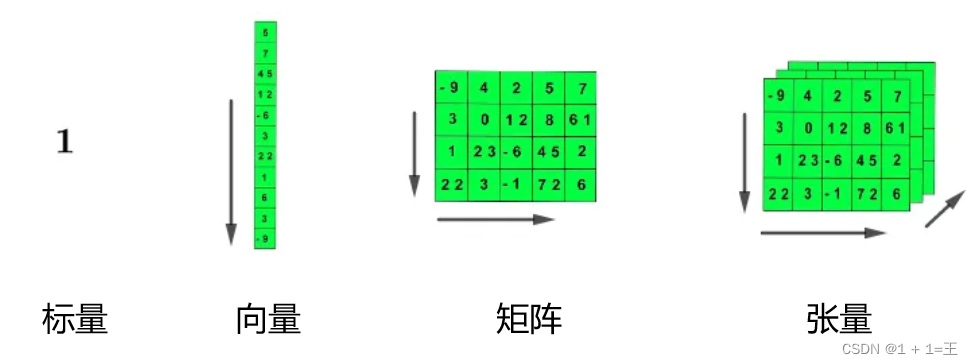
- 标量(scalar):一个单独的数。
- 向量(vector):⼀组有序排列的数。通过次序中的索引,我们可以确定每个单独的数。
- 矩阵(matrix):具有相同特征和纬度的对象的集合。⼀个对象表⽰为矩阵中的⼀⾏,⼀个特征表⽰为矩阵中的⼀列,表现为⼀张⼆维数据表。
- 张量(tensor):一个多维数组,⼀个数组中的元素分布在若⼲维坐标的规则⽹格中,我们将其称之为张量。
向量范数和矩阵的范数
向量范数
设一个向量 ,不同范数表示如下:
,不同范数表示如下:
-
向量的1范数:向量的各个元素的绝对值之和
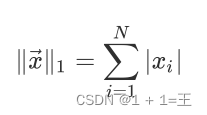
-
向量的2范数:向量的每个元素的平⽅和再开平⽅根
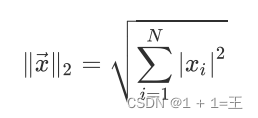
-
向量的负⽆穷范数:向量的所有元素的绝对值中最小的
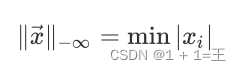
-
向量的正⽆穷范数:向量的所有元素的绝对值中最大的
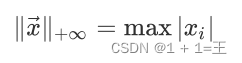
-
向量的p范数:
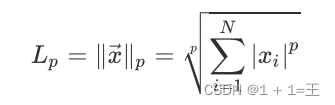
矩阵范数
设矩阵定义为Amxn,其元素为aij。
-
矩阵的1范数(列范数):矩阵的每⼀列上的元素绝对值先求和,再从中取个最⼤的,(列和最⼤)。
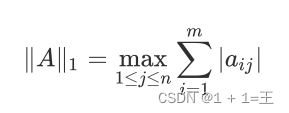
-
矩阵的2范数:矩阵ATA的最大特征值开平方根。
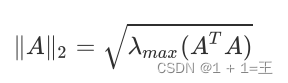
-
矩阵的⽆穷范数(⾏范数):矩阵的每⼀⾏上的元素绝对值先求和,再从中取个最⼤的,(⾏和最⼤)。
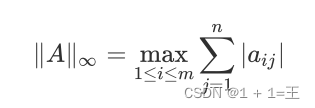
-
矩阵的L0范数:矩阵的⾮0元素的个数
-
矩阵的L1范数: 矩阵中的每个元素绝对值之和
-
矩阵的F范数: 矩阵的各个元素平⽅之和再开平⽅根,它通常也叫做矩阵的L2范数。

-
矩阵的p范数:
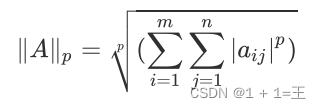
导数和偏导数
导数代表了在⾃变量变化趋于⽆穷⼩的时候,函数值的变化与⾃变量的变化的⽐值。⼏何意义是这个点的切线。物理意义是该时刻的(瞬时)变化率。
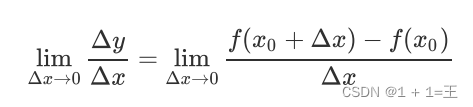
偏导数就是指多元函数沿着坐标轴的变化率。
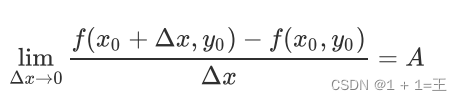
特征值和特征向量
特征值表⽰的是这个特征到底有多重要,⽽特征向量表⽰这个特征是什么。
如果说⼀个向量ν是矩阵A的特征向量,将⼀定可以表⽰成下⾯的形式:
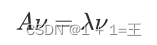
λ为特征向量ν对应的特征值。即矩阵A的信息可以由其特征值和特征向量表⽰。
概率分布
伯努利分布
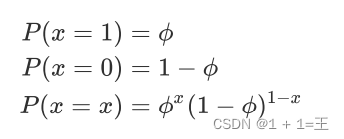
期望:φ, 方差:φ(1-φ)
正态分布(高斯分布)
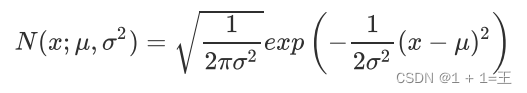
期望:μ, 方差:φ
缺乏实数上分布的先验知识, 不知选择何种形式时, 默认选择正态分布。
指数分布
深度学习中, 指数分布⽤来描述在 点处取得边界点的分布:
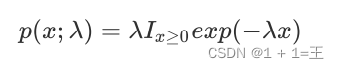
期望、⽅差、协⽅差、相关系数
期望
数学期望是试验中每次可能结果的概率乘以其结果的总和。它反映随机变量平均取值的⼤⼩。
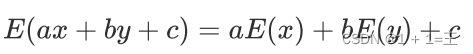
-
离散函数
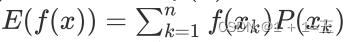
-
连续函数
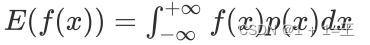
方差
⽅差⽤来度量随机变量和其数学期望之间的偏离程度。
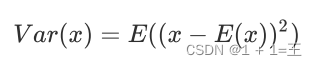
协⽅差
协⽅差是衡量两个变量线性相关性强度及变量尺度。
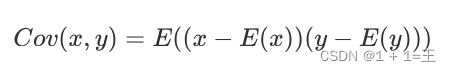
相关系数
相关系数是研究变量之间线性相关程度的量。