做商城，流量必不可少，日活跃度也很重要。现在各大APP、网站、小程序和微商城，基本都在为了巩固流量做积分商城，虽然已经随处可见，但很多企业商家却并没有将积分商城运作起来，积分商城也没有人浏览兑换商品。那积分商城究竟该怎么运作？做积分商城又有哪些需要注意的呢？

积分商城的玩法

1、兑换商品

如今，积分商城最常见的玩法就是兑换商品，兑换的商品可以是实物类商品，也可以是优惠券等虚拟类商品，如需展现品牌价值，还可以提供企业定制商品。

积分商城可兑换的商品需要不断丰富、定期更新，持续吸引用户关注，企业也可以根据用户特征选择商品，选择口碑不错、复购率较高的商品。

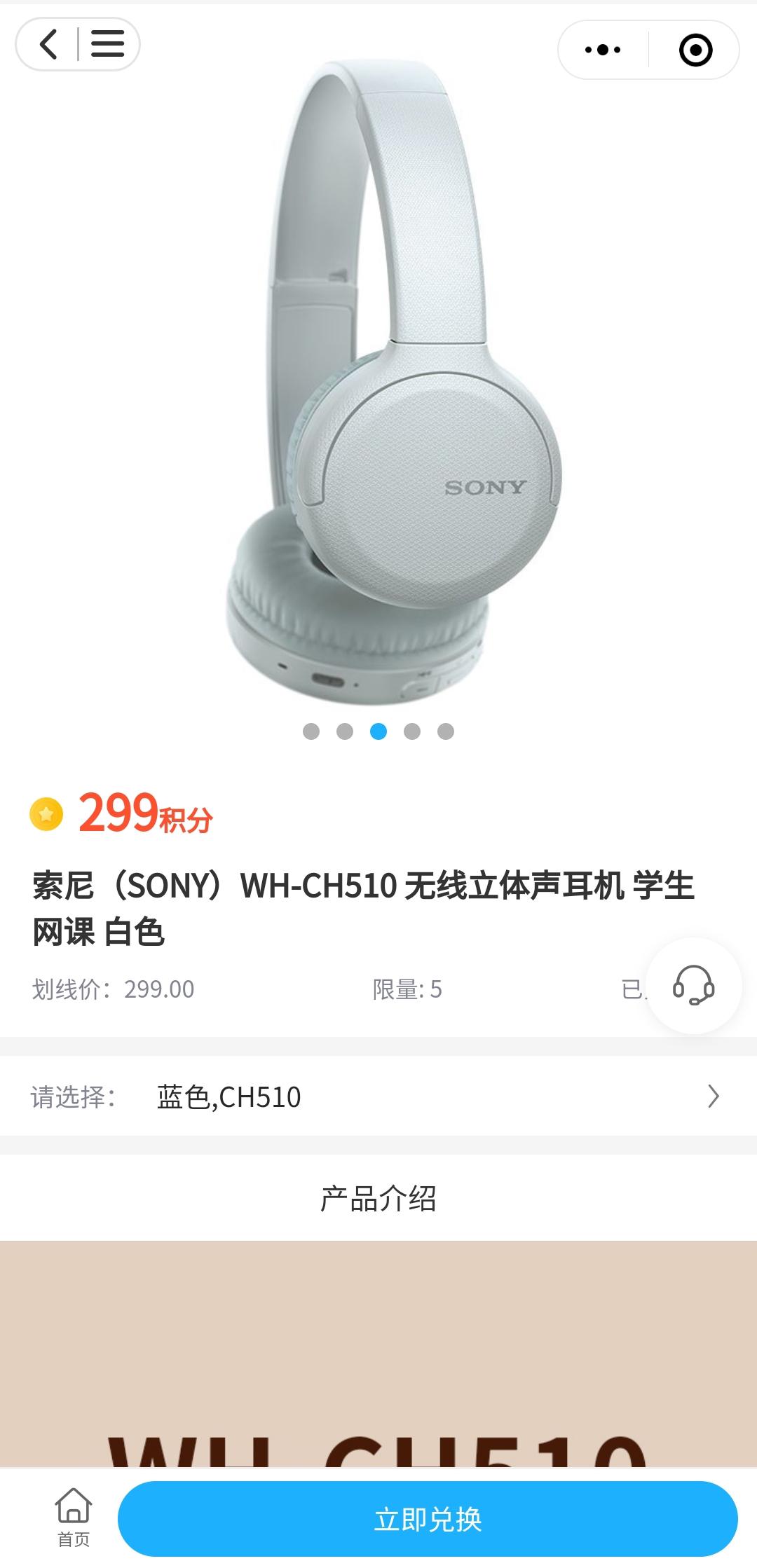
CRMEB标准版积分兑换礼品

2、积分抽奖

不同价值的商品兑换所需积分应进行区分，对于手机、大牌美妆等高价值的商品，可以将消费模式从兑换改成抽奖，既降低了企业成本负担，也能降低活动参与门槛，提高用户的积极性。

除抽奖外，还有很多积分小游戏，可以使用少量积分参与，也和积分抽奖有类似的作用。

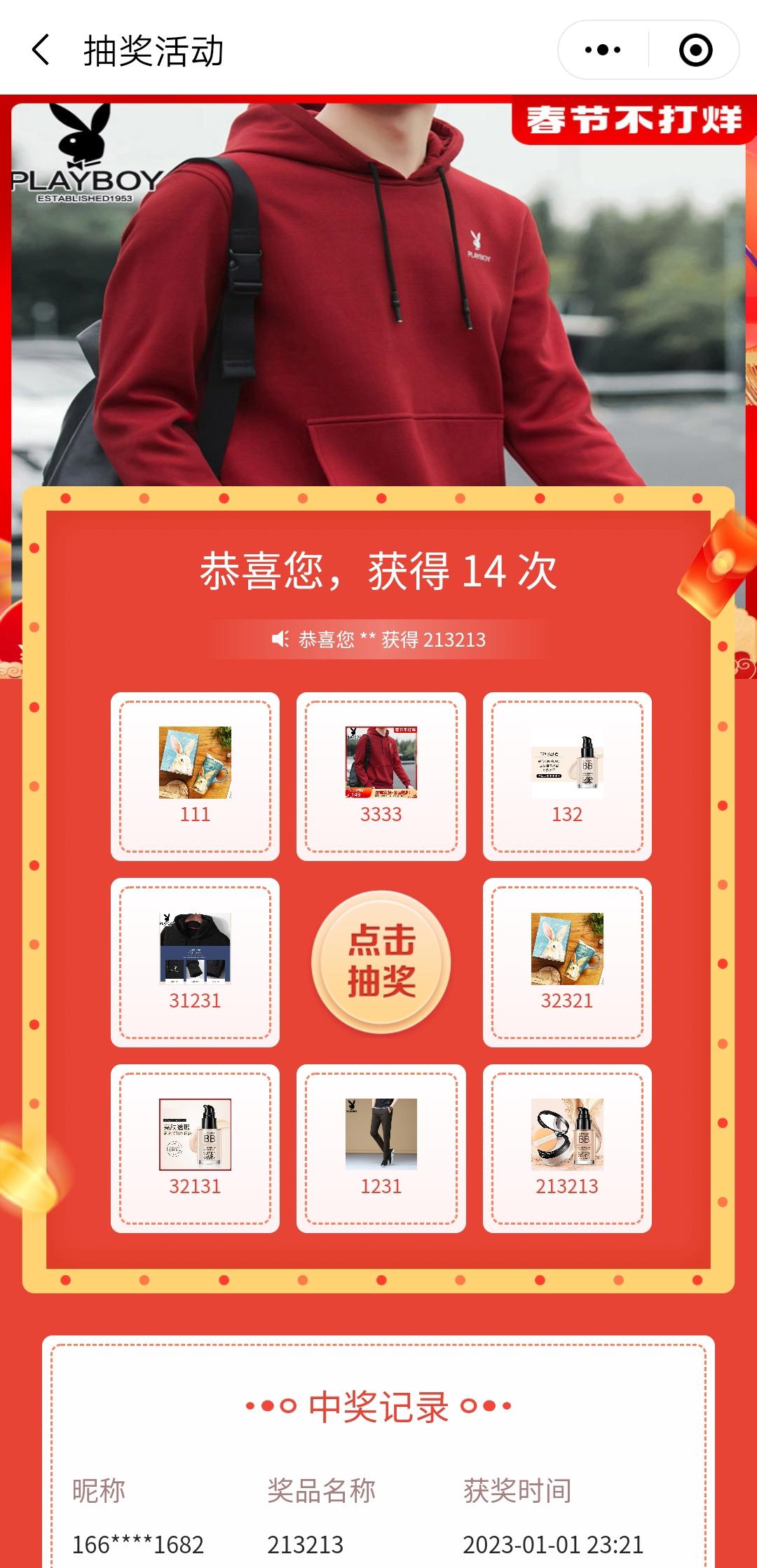
CRMEB标准版积分抽奖页面演示

3、卡券营销

这类玩法一般会推出积分兑换优惠券的活动，用户用账户积分兑换店铺优惠券，有的也可以享受满减、折扣等权益，这种玩法有助于吸引用户复购。

4、会员+积分

现在，无论大平台还是小品牌都有会员体系，单纯的会员管理已经对消费者失去吸引力，所以，会员+积分的用户管理形式开始盛行。

会员+积分形式，可以为消费者提供会员等级积分权益、用户关怀、会员专享积分兑换好礼等福利，积分的加入，让会员的参与方式更加多样，也能帮助商家留存用户并进行拉新。

积分商城的运营策略

1、积分商城要重视运营

要把积分商城做好，不是把系统做好上线就行。相比系统搭建，积分商城的运营更为重要。积分商城运营的目的是为了更好的维护用户，所以，积分获取渠道、积分兑换规则、兑换商品设置、用户数据统计分析、商品供应及物流保障、积分客服售后服务等问题都需要后期持续稳定的运营。

2、兑换商品品质种类两手抓

积分商城最常见的玩法就是兑换商品，平台商品代表的是企业的形象，如果积分兑换的商品质量不好，很容易让消费者反感，甚至流失客户。

所以，在管理积分商城商品时，要充分考虑用户的行业、年龄特征，商品种类要尽量丰富，尽量满足不同用户的需求，同时，也要保障商品的质量，让用户信任品牌，更容易吸引用户复购。

3、积分合理分配

积分商城的目的是为了让用户消耗积分、优惠券等，养成重复使用系统的习惯，所以，合理设置积分规则也很重要。企业不仅需要考虑哪些活动要让用户获得积分，也要设置相应的活动，让用户去消耗积分。

4、数据统计要重视

企业要做好商城的每日消耗积分、热门积分兑换商品、每日兑换商品统计及用户行为分析，有利于完善用户画像，优化运营策略，持续提供更好的服务。

通过运营积分商城，可以实现用户激活、留存、拉新及盈利，但现在很多平台的积分商城都只是摆设，没有好好利用起来，平台用户的积分使用率都很低。

所以，重视积分商城的运营管理，抓住积分商城的主要目的，梳理用户行为路径，促进用户的日活和粘性，才能形成积分商城的良性循环，也能逐渐让积分商城活跃起来，体现出积分商城的价值和魅力。