basic paxos 是用于确定且只能确定一个值,“只确定一个值有什么用?这可解决不了我面临的问题,例如每个用户都要多次保存数据.” 你心中可能有这样的疑问。
原simple paxos论文里有提到一连串个instance of paxos [4] 但没有提出 multi paxos的概念,原simple paxos有提出多leader的方式,目的只是减少 proposer 的数量,为了降低单一paxos过程中的死锁问题,并不是为了提高multi-paxos的效率。 实际上multi paxos是由谷歌提出的[3]. zk和raft也都是multi paxos,且使用了唯一leader的方式,将经典paxos的两次半数过程变成了仅一次半数过程。
simple paxos论文的实现很复杂,虽然有leader,但每次还是basic paxos. 但zk,raft中的实现是对basic paxos又一次创造性优化,各个instances复用了prepare阶段的半数约束(即leader的产生是通过prepare的半数约束产生的). 详细讲解见下文
正常的存储系统其实不断地进行“确定一个值”的过程、再为每个过程编上序号,就能得到具有全序关系(total order)的系列值,进而能应用在数据库副本存储等很多场景。我们把单次“确定一个值”的过程称为实例(instance),它由proposer/acceptor/learner组成,下图说明了A/B/C三机上的实例:
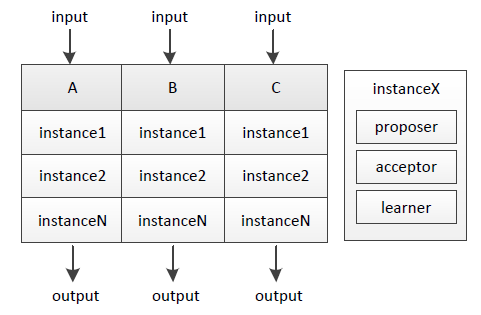
不同序号的实例之间互相不影响,A/B/C三机输入相同、过程实质等同于执行相同序列的状态机(state machine)指令 ,因而将得到一致的结果。
如何实现?(by phil)
1. 方法一,比较差的.延续basic paxos的思路.
每个分布式存储server接受到client请求后,就提出议案. 有可能别人也在提. 那就各自抢,看谁的议案先被通过. 通过后如果没有新的client请求,就不提案了.其他机器接着提"提案". 这里"提案"就是客户端请求的"命令". 这样命令之间的顺序就确认了.
2. 方案二, 上面那个方案性能太差了.
缺点:
1. 每次请求都有可能互相争抢
2.有些请求明明可以并发的也不能并发了.例如对不同的key修改值.
改进:
增加一个leader,把所有的命令都提交给leader,然后leader再进行提案申请. 如果leader不能排他, 提案仍旧需要进行basic paxos. 而且也无法知道是否操作的是相同的key. 不能并发.
核心问题: leader是否是排他的?
再改进:
做不到leader排他,但是可以将"leader选举结果"作为所有后面提案basic paxos的共同"prepare 部分". 这样及时有一个leader最终变成了假leader,即basic paxos的加锁失败. 问题也不大. 其提案的值也不会被认可.
这就是zk的zab 和 ltcd的raft 使用的方案.
不过他们选举leader的方式不太一致. 并且zk是通过队列保证一致的. raft是通过连续的序号保持一致的.类似 simple paxos里的例子.[1]
note: leader的选举不一定要是paxos完整paxos协议. 不一定严格排他的. 毕竟你认为已经大多数是历史时刻的,有可能会改变.
proposer leader在Multi Paxos中还有助于提升性能,常态下统一由leader发起提议,可节省prepare步骤(leader不用问询acceptor曾接受过的ID最大的提议、只有leader提议也不需要acceptor进行promise)直至发生leader宕机、重新选主。
小结
以上介绍了Paxos的推演过程、如何在Basic Paxos的基础上通过状态机构建Multi Paxos。Paxos协议比较“艰深晦涩”,但多读几遍论文一般能理解其内涵,更难的是如何将Paxos真正应用到工程实践。
微信后台开发同学实现并开源了一套基于Paxos协议的多机状态拷贝类库PhxPaxos,PhxPaxos用于将单机服务扩展到多机,其经过线上系统验证并在一致性保证、性能等方面作了很多考量。
[1] Paxos算法与Zookeeper分析,raft协议,ltcd 8. 与Galera及MySQL Group replication的比较 https://www.cnblogs.com/fei33423/p/7888503.html
[2] 分布式系统理论进阶 - Paxos 和multi paxos 大部分摘抄自这里
[3] Blockchain的鱼和熊掌系列(9)Multi-Paxos协议 http://blog.csdn.net/Canhui_WANG/article/details/54981593
[4] 第三节第二段 we implement a sequence of separate instances of the Paxosconsensus algorithm https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/paxos-simple-Copy.pdf



![剑指 Offer 10- I. 斐波那契数列[c语言]](https://img-blog.csdnimg.cn/3c7b7485e07343e3b924653d1109d8ce.png)