05- 线性回归算法 (LinearRegression) (算法)

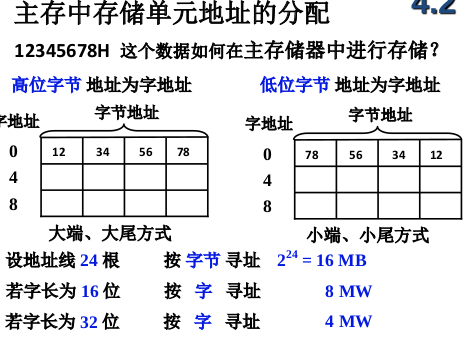
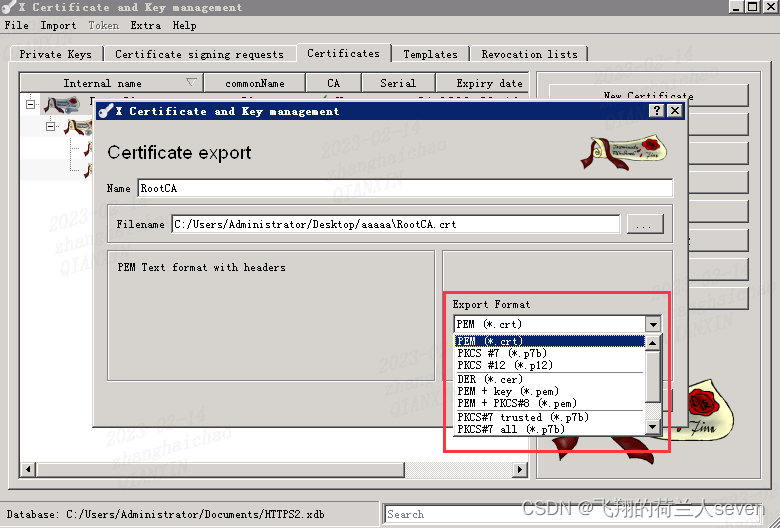
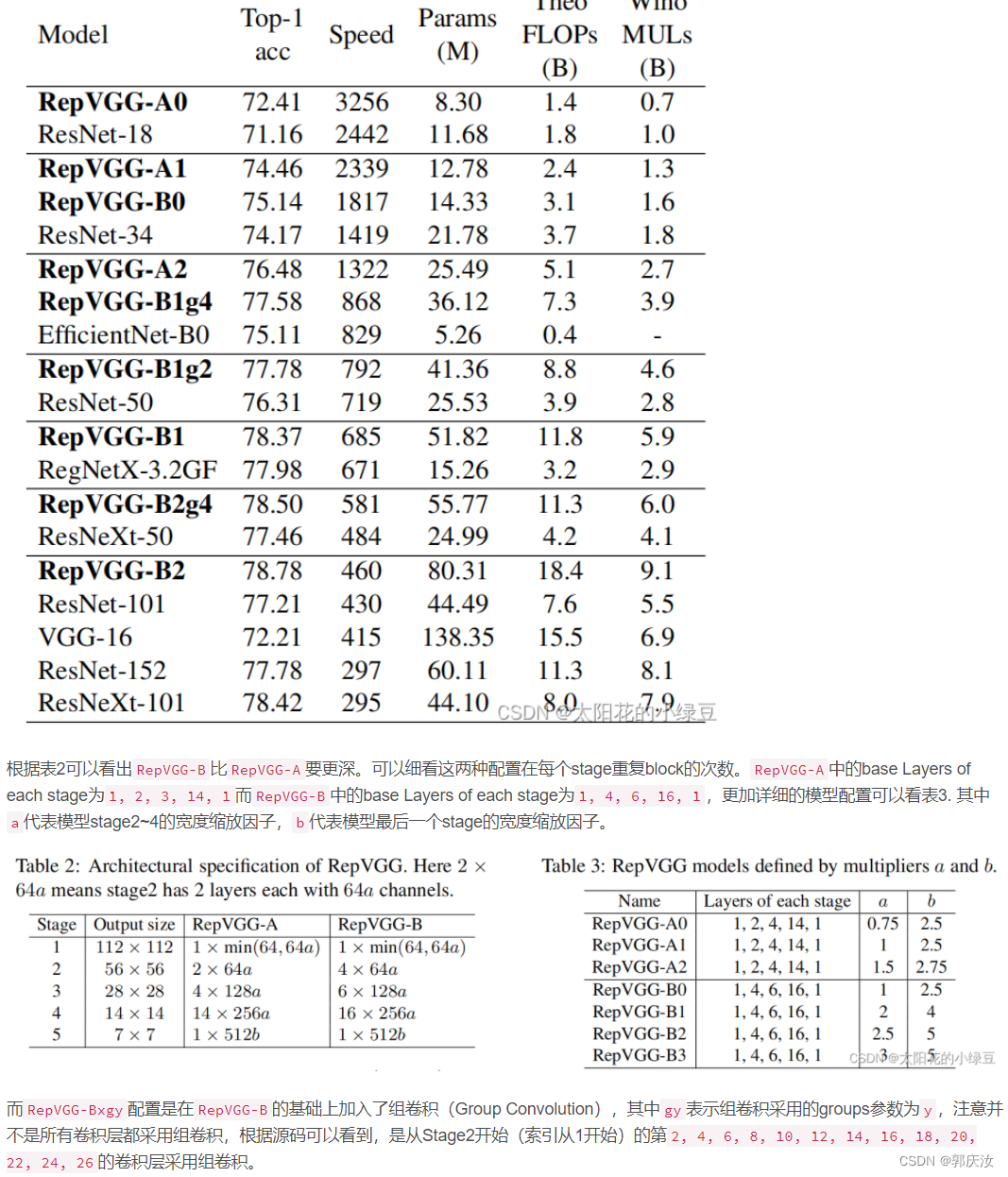
线性回归算法(LinearRegression)就是假定一个数据集合预测值与实际值存在一定的误差, 然后假定所有的这些误差值符合正太分布, 通过方程求这个正太分布的最小均值和方差来还原原数据集合的斜率和截距。
当误差值无限接近于0时, 预测值与实际值一致, 就变成了求误差的极小值。

from sklearn.linear_model import LinearRegression   
model = LinearRegression()   # 使用模型
model.fit(X,y)

w_ = model.coef_        # 斜率
b_ = model.intercept_   # 截距

θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2) # [[3.97] [7.19]] 矩阵求解

1、基本概念

线性回归是机器学习中有监督机器学习下的一种算法。 回归问题主要关注的是因变量(需要预测的值，可以是一个也可以是多个)和一个或多个数值型的自变量(预测变量)之间的关系。

需要预测的值:即目标变量，target，y，连续值预测变量。
影响目标变量的因素： $X_1...X_n$ ，可以是连续值也可以是离散值。
因变量和自变量之间的关系:即模型，model，是我们要求解的。

1.1、连续值和离散值

比如人的身高和全国的省份分布

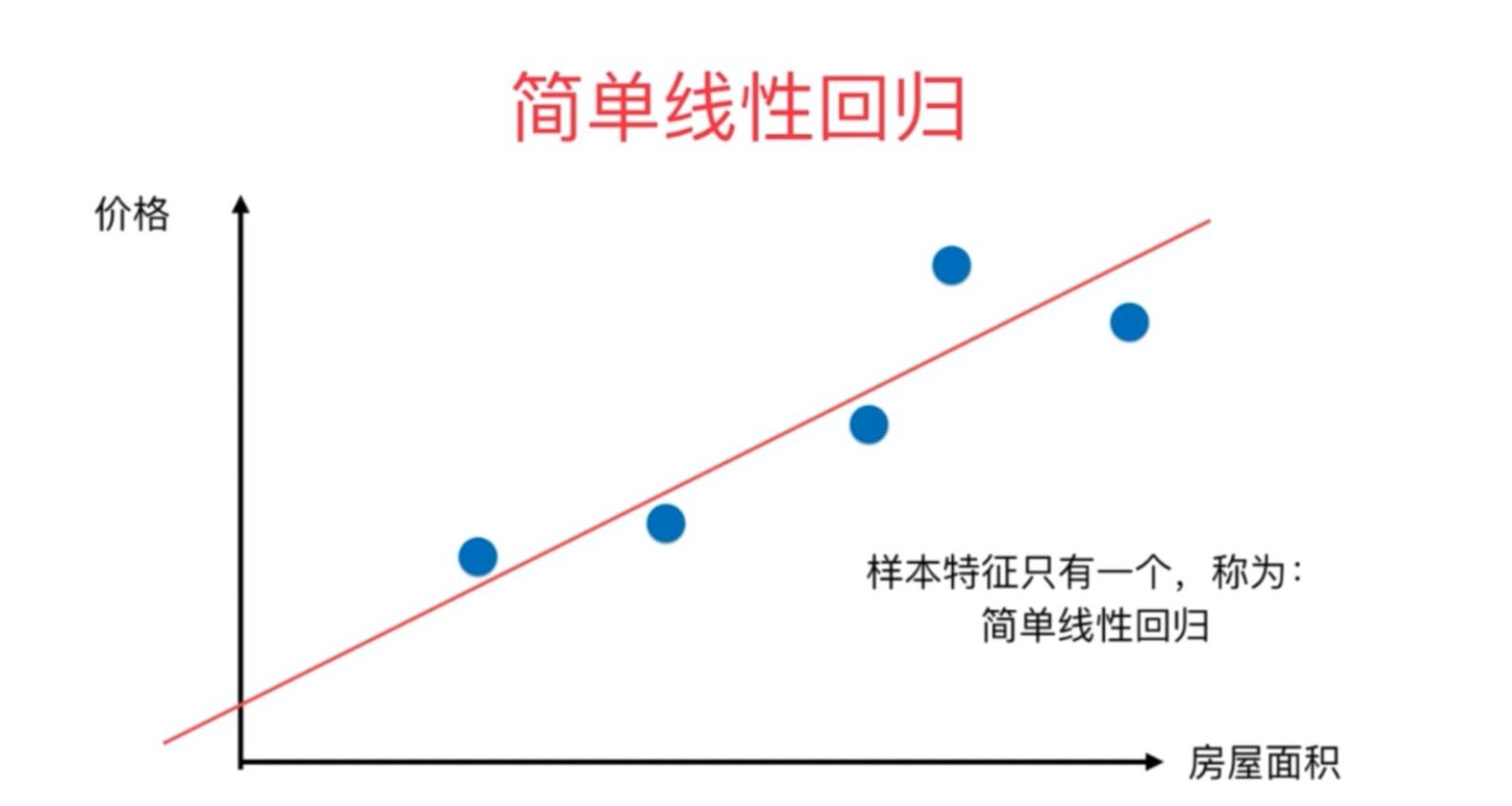
1.2、简单线性回归

简单线性回归属于一个算法，它所对应的公式。

$y = wx + b$

1.3、最优解

最优解:尽可能的找到一个模型使得整体的误差最小，整体的误差通常叫做损失 Loss。

Actual value: 真实值，一般使用 y 表示，实际值。
Predicted value: 预测值，是把已知的 x 带入到公式里面和猜出来的参数 w,b 计算得到的，一般使用y_表示。
error: 误差，预测值和真实值的差距，一般使用 ϵ 表示。
最优解: 尽可能的找到一个模型使得整体的误差最小，整体的误差通常叫做损失 Loss。
Loss: 整体的误差，Loss 通过损失函数 Loss function 计算得到。

1.4、多元线性回归

现实生活中，往往影响结果 y 的因素不止一个，这时 x 就从一个变成了 n 个，X1,X2…Xn同时简单线性回归的公式也就不在适用了。多元线性回归公式如下：

$\hat{y} = w_1x_1 + w_2x_2 +.....+ w_nx_n + b$

b是截距，也可以使用来表示

$\hat{y} = w_1x_1 + w_2x_2 + ...... + w_nx_n + w_0$
使用向量来表示， $\vec{X}$ 表示所有的变量，是一维向量； $\vec{W}$ 表示所有的系数（包含 $w_0$ ），是一维向量，根据向量乘法规律:

${\color{Red} \hat{y} = W^TX}$

2、正规方程

2.1、最小二乘法矩阵表示

最小二乘法可以将误差方程转化为有确定解的代数方程组（其方程式数目正好等于未知数的个数），从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。公式如下：

$\theta = (X^TX)^{-1}X^Ty$ 或者 ${\color{Red} W = (X^TX)^{-1}X^Ty}$ ，其中的 $W$ 和 $\theta$ 即使方程的解！

最小二乘法公式:

${\color{Red} J(\theta) = \frac{1}{2}\sum\limits_{i = 0}^n(h_{\theta}(x_i) - y_i)^2}$

使用矩阵表示:

2.2、多元一次方程举例

三元一次方程 :

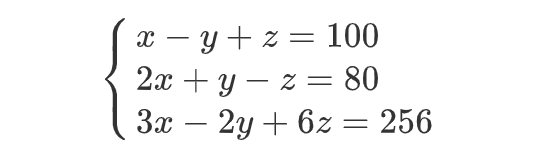
通过矩阵可以直接求解: ${\color{Red} W = X^{-1}Y}$ # 通过逆矩阵进行求解

# 上面八元一次方程对应的X数据
X = np.array( [[1, -1, 1], [2, 1, -1], [2, -2, 6]])
# 对应的y
y = np.array([100, 80, 256])
np.linalg.solve(X,y).round(2)  # array([ 60., -26.,  14.])

2.3、推导正规方程 ${\color{DarkBlue} \theta}$ 的解

矩阵乘法公式展开

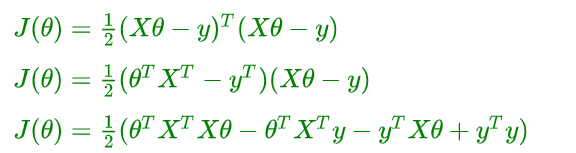
使用逆矩阵进行转化

2.4、凸函数判定

判定损失函数是凸函数的好处在于我们可能很肯定的知道我们求得的极值即最优解，一定是全局最优解。

判定凸函数的方式: 判定凸函数的方式非常多，其中一个方法是看黑塞矩阵是否是半正定的。

黑塞矩阵(hessian matrix)是由目标函数在点 X 处的二阶偏导数组成的对称矩阵。在导函数的基础上再次对θ来求偏导，结果全为正时为正定,如果结果大于等于0, 就是半正定。判定极小值.

在机器学习中往往损失函数都是凸函数，到深度学习中损失函数往往是非凸函数，即找到的解未必是全局最优，只要模型堪用就好！机器学习特点是：不强调模型 100% 正确，只要是有价值的，堪用的，就Okay！

3、线性回归算法推导

人类社会很多事情都被大自然这种神奇的力量只配置：身高、体重、智商、相貌……这种神秘的力量就叫正态分布。大数学家高斯，深入研究了正态分布，最终推导出了线性回归的原理：最小二乘法！

3.1、误差分析

误差等于第 i 个样本实际的值减去预测的值，公式可以表达为如下：
${\color{Red} \varepsilon_i = |y_i - \hat{y}|}$ 或 $\varepsilon_i = |y_i - W^Tx_i|$
假定所有的样本的误差都是独立的，有上下的震荡，震荡认为是随机变量，足够多的随机变量叠加之后形成的分布，它服从的就是正态分布，因为它是正常状态下的分布，也就是高斯分布！均值是某一个值，方差是某一个值。方差我们先不管，均值我们总有办法让它去等于零 0 的，因为我们这里是有截距b，所有误差我们就可以认为是独立分布的，1<=i<=n，服从均值为 0，方差为某定值的高斯分布。机器学习中我们假设误差符合均值为0，方差为定值的正态分布.将误差定义到正太分布中.当样本足够多的时候,取样本的均值则为实际值.

3.2、最大似然估计

最大似然估计(maximum likelihood estimation, MLE)一种重要而普遍的求估计量的方法。最大似然估计明确地使用概率模型，其目标是寻找能够以较高概率产生观察数据的系统发生树。最大似然估计是一类完全基于统计的系统发生树重建方法的代表。

3.3、高斯分布-概率密度函数

最常见的连续概率分布是正态分布，也叫高斯分布，而这正是我们所需要的，其概率密度函数如下:

正态分布 公式如下：

随着参数μ和σ变化，概率分布也产生变化。下面重要的步骤来了，我们要把一组数据误差出现的总似然，也就是一组数据之所以对应误差出现的整体可能性表达出来了，因为数据的误差我们假设服从一个高斯分布，并且通过截距项来平移整体分布的位置从而使得μ=0.

3.4、误差总似然, 最小二乘法MSE

这种最小二乘法估计，其实我们就可以认为，假定了误差服从正太分布，认为样本误差的出现是随机的，独立的，使用最大似然估计思想，利用损失函数最小化 MSE 就能求出最优解！所以反过来说，如果我们的数据误差不是互相独立的，或者不是随机出现的，那么就不适合去假设为正太分布，就不能去用正太分布的概率密度函数带入到总似然的函数中，故而就不能用 MSE 作为损失函数去求解最优解了！
还有譬如假设误差服从泊松分布，或其他分布那就得用其他分布的概率密度函数去推导出损失函数了。
所以有时我们也可以把线性回归看成是广义线性回归。比如，逻辑回归，泊松回归都属于广义线性回归的一种，这里我们线性回归可以说是最小二乘线性回归。

4、线性回归实战

4.1、简单线性回归

一元一次方程，在机器学习中一元表示一个特征，b表示截距，y表示目标值。

import numpy as np
import matplotlib.pyplot as plt
# 转化成矩阵
X = np.linspace(0,10,num = 30).reshape(-1,1)
# 斜率和截距，随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)
# 根据一元一次方程计算目标值y，并加上“噪声”，数据有上下波动~
y = X * w + b + np.random.randn(30,1)
plt.scatter(X,y)
# 重新构造X，b截距，相当于系数w0，前面统一乘以1
X = np.concatenate([X,np.full(shape = (30,1),fill_value= 1)],axis = 1)
# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2)  # 根据公式计算
print('一元一次方程真实的斜率和截距是：',w, b)
print('通过正规方程求解的斜率和截距是：',θ)
# 根据求解的斜率和截距绘制线性回归线型图
plt.plot(X[:,0],X.dot(θ),color = 'green')

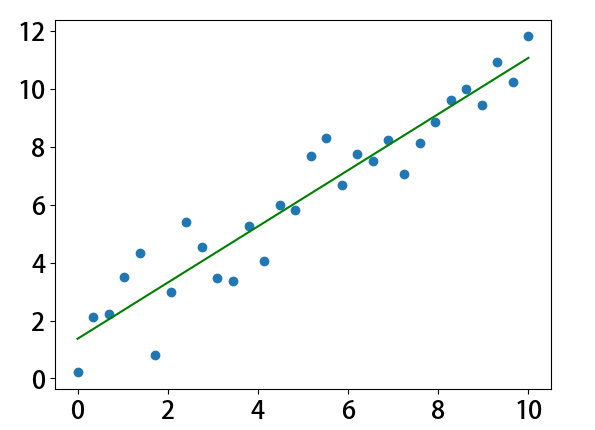
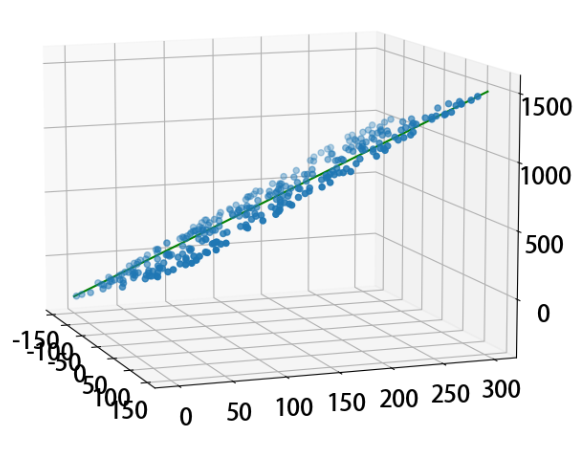
4.2、多元线性回归

二元一次方程，x1, x2相当于两个特征，b是方程截距

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D # 绘制三维图像
# 转化成矩阵
x1 = np.random.randint(-150,150,size = (300,1))
x2 = np.random.randint(0,300,size = (300,1))
# 斜率和截距，随机生成
w = np.random.randint(1,5,size = 2)
b = np.random.randint(1,10,size = 1)
# 根据二元一次方程计算目标值y，并加上“噪声”，数据有上下波动~
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300,1)
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
# 重新构造X，将x1、x2以及截距b，相当于系数w0，前面统一乘以1进行数据合并
X = np.concatenate([x1,x2,np.full(shape = (300,1),fill_value=1)],axis = 1)
w = np.concatenate([w,b])
# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2)  # 计算公式
print('二元一次方程真实的斜率和截距是：',w)
print('通过正规方程求解的斜率和截距是：',θ.reshape(-1))
# # 根据求解的斜率和截距绘制线性回归线型图
x = np.linspace(-150,150,100)
y = np.linspace(0,300,100)
z = x * θ[0] + y * θ[1] + θ[2]
ax.plot(x,y,z ,color = 'red')

4.3、机器学习库scikit-learn

一元线性回归:

from sklearn.linear_model import LinearRegression   
import numpy as np
import matplotlib.pyplot as plt
# 转化成矩阵
X = np.linspace(0,10,num = 30).reshape(-1,1)
# 斜率和截距，随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)
# 根据一元一次方程计算目标值y，并加上“噪声”，数据有上下波动~
y = X * w + b + np.random.randn(30,1)
plt.scatter(X,y)
# 使用scikit-learn中的线性回归求解
model = LinearRegression()   # 使用模型
model.fit(X,y)
w_ = model.coef_
b_ = model.intercept_
print('一元一次方程真实的斜率和截距是：',w, b)
print('通过scikit-learn求解的斜率和截距是：',w_,b_)
plt.plot(X,X.dot(w_) + b_,color = 'green')

多元线性回归:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
from sklearn.linear_model import LinearRegression  
# 转化成矩阵
x1 = np.random.randint(-150,150,size = (300,1))
x2 = np.random.randint(0,300,size = (300,1))
# 斜率和截距，随机生成
w = np.random.randint(1,5,size = 2)
b = np.random.randint(1,10,size = 1)
# 根据二元一次方程计算目标值y，并加上“噪声”，数据有上下波动~
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300,1)
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
# 重新构造X，将x1、x2以及截距b，相当于系数w0，前面统一乘以1进行数据合并
X = np.concatenate([x1,x2],axis = 1)
# 使用scikit-learn中的线性回归求解
model = LinearRegression()   # 使用模型
model.fit(X,y)
w_ = model.coef_.reshape(-1)
b_ = model.intercept_
print('二元一次方程真实的斜率和截距是：',w,b)     # [2, 4] [1]
print('通过scikit-learn求解的斜率和截距是：',w_,b_)   # [1.99997 3.99976] [0.88129]
# 根据求解的斜率和截距绘制线性回归线型图
x = np.linspace(-150,150,100)
y = np.linspace(0,300,100)
z = x * w_[0] + y * w_[1] + b_
ax.plot(x,y,z ,color = 'green')