前端开发：关于diff算法详解

news2024/11/24 9:21:39

前言

前端开发中，关于JS原生的内容和前端算法相关的内容一直都是前端工作中的核心，不管是在实际的前端业务开发还是前端求职面试，都是非常重要且必备的内容。那么本篇博文来分享一个关于前端开发中必备内容：diff算法，diff算法在前端实战中和前端求职面试中都是必备知识，整理总结一下，方便查阅使用。

diff算法是什么？

diff算法其实就是用于比较新旧虚拟DOM节点的差异性的算法。众所周知，每一个虚拟DOM节点都会有一个唯一标识，即Key，diff算法把树形结构按照层级分解，只比较同级元素，不同层级的节点只有创建和删除操作，通过对比新旧节点的Key来判断当前节点是否改变，把两个节点不同的地方存储在patch对象中，然后利用patch记录的消息进行局部更新DOM操作。

注意：若输入的新节点不是虚拟DOM , 那么需要将DOM节点转换为虚拟DOM才行，也就是说diff算法是针对虚拟DOM的。

patch()函数

patch函数其实就是用于节点上树，更新DOM的函数，也就是将新旧节点进行比较的函数。

diff算法的诞生

想必大家都知道，前端领域中在之前传统的DOM操作非常昂贵，数据的改变往往需要更新 DOM 树上的多个节点，可谓是牵一发而动全身，所以虚拟DOM和Diff算法的诞生就是为了解决上述问题。

前端的Web界面由 DOM 树来构成，当某一部分发生变化的时候，其实就是对应的某个 DOM 节点发生了变化。在 Vue中，构建 UI 界面的思路是由当前状态决定界面，前后两个状态就对应两套界面，然后由 Vue来比较两个界面的区别，本质是比较 DOM 节点差异当两个节点不同时应该如何处理，分为两种情况：一、节点类型不同；二、节点类型相同，但是属性不同。了解它们就需要对 DOM 树进行 Diff 算法分析。

diff算法的优势

diff算法的性能优势在于对比新旧两个 DOM节点的不同的时候，只对比同一级别的 DOM 节点，一旦发现有不同的地方，后续的DOM子节点将被删掉而不再作对比操作。使用diff算法提高了更新DOM的性能，不用再把整个页面全部删除后重新渲染；使用diff算法让虚拟DOM只包括必须的属性，不再把真实DOM的全部属性都拿出来。

diff算法的示例

这里先来以Vue来介绍一下diff算法的示例，这里直接在vue文件的模板中进行一个简单的标签实现，需要被vue处理成虚拟DOM，然后渲染到真实DOM中，具体代码如下所示：

//标签设置

<template>
<div id="content">
<p class="sonP">Hello</p>
</div>
</template>

//相对应的虚拟DOM结构

const dom = {

type: 'div',

attributes: [{id: 'content'}],

children: {

type: 'p',

attributes: [{class: 'sonP'}],

text: 'Hello'

}

}

通过上面的代码演示可以看到，新建标签之后，系统内存中会生成对应的虚拟DOM结构，由于真实DOM属性有很多，无法快速定位是哪个属性发生改变，然后通过diff算法能够快速找到发生变化的地方，然后只更新发生变化的部分渲染到页面上，也叫打补丁。

虚拟DOM

虚拟DOM是保存在程序内存中的，它只记录DOM的关键信息，然后结合diff算法来提高DOM更新的性能操作，在程序内存中比较差异，最后给真实DOM打补丁更新操作。

diff算法的比较规则

diff算法在进行比较操作的规则是这样的：

新节点前和旧节点前；
新节点后和旧节点后；
新节点后和旧节点前；
新节点前和旧节点后。

只要符合一种情况就不会再进行判断，若没有符合的，就需要循环来寻找，移动到旧前之前操作。结束查找的前提是：旧节点前新节点前。

diff算法的三种比较方式

diff算法的比较方式有三种，分别如下所示：

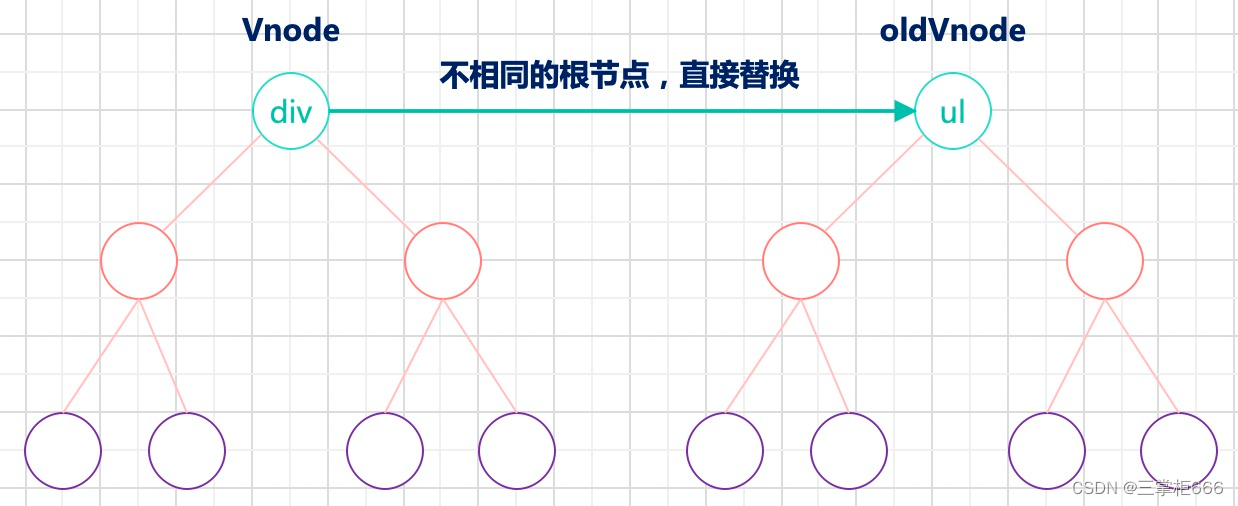
方式一：根元素发生改变，直接删除重建

也就是同级比较，根元素发生改变，整个DOM树会被删除重建。如下示例：

//旧的虚拟DOM

<ul id="content">
<li class="sonP">hello</li>
</ul>

//新的虚拟DOM

<div id="content">
<p class="sonP">hello</p>
</div>

方式二：根元素不变，属性改变，元素复用，更新属性

这种方式就是在同级比较的时候，根元素不变，但是属性改变之后更新属性，示例如下所示：

//旧的虚拟DOM

<div id="content">
<p class="sonP">hello</p>
</div>

//新的虚拟DOM

<div id="content" title="hello">
<p class="sonP">hello</p>
</div>

方式三：根元素不变，子元素不变，元素内容发生变化

也就是根元素和子元素都不变，只是内容发生改变，这里涉及到三种小的情况：无Key直接更新、有Key但以索引为值、有Key但以id为值。

1、无Key直接更新

无Key直接就地更新，由于v-for不会移动DOM，所以只是尝试复用，然后就地更新；若需要v-for来移动DOM，则需要用特殊 attribute key 来提供一个排序提示。示例如下所示：

<ul id="content">
<li v-for="item in array">
{{ item }}
<input type="text">
</li>
</ul>
<button @click="addClick">在下标为1的位置新增一行</button>
export default {
data(){
return {
array: ["11", "44", "22", "33"]
}
},
methods: {
addClick(){
this.array.splice(1, 0, '44')
}
}
};

2、有Key但以索引为值

这里也是直接就地更新，通过新旧虚拟DOM对比，key存在就直接复用该标签更新的内容，若key不存在就直接新建一个。示例如下所示：

<ul id="content">
<li v-for="(item, index) in array" :key="index">
{{ item }}
<input type="text">
</li>
</ul>
<button @click="addClick">在下标为1的位置新增一行</button>
export default {
data(){
return {
array: ["11", "44", "22", "33"]
}
},
methods: {
addClick(){
this.array.splice(1, 0, '44')
}
}
};

通过上面代码可以看到，通过v-for循环产生新的DOM结构, 其中key是连续的, 与数据对应一致，然后比较新旧DOM结构, 通过diff算法找到差异区别, 接着打补丁到页面上，最后新增补一个li，然后从第二元素以后都要更新内容。

3、有Key但以id为值

由于Key的值只能是唯一不重复的，所以只能以字符串或数值来作为key。由于v-for不会移动DOM，所以只是尝试复用，然后就地更新；若需要v-for来移动DOM，则需要用特殊 attribute key 来提供一个排序提示。

若新DOM数据的key存在, 然后去旧的虚拟DOM里找到对应的key标记的标签, 最后复用标签；若新DOM数据的key存在, 然后去旧的虚拟DOM里没有找到对应的key标签的标签，最后直接新建标签；若旧DOM结构的key, 在新的DOM结构里不存在了, 则直接移除对应的key所在的标签。

<ul id="content">
<li v-for="object in array" :key="object.id">
{{ object.name }}
<input type="text">
</li>
</ul>
<button @click="addClick">在下标为1的位置新增一行</button>
export default {
data(){
return {
array: [{id:11,name:"11"}, {id:22,name:"22"}, {id:33,name:"33"}]
}
},
methods: {
addClick(){
this.array.splice(1, 0,{id:44,name: '44'})
}
}
};