开启第二课！

目录

1.神经网络概述

2 前向传播（forward propogation）神经网络

3. tensorflow实现

 Numpy中的matrix：

用循环写NN：

​用numpy写NN:​

 AGI​

关于矩阵运算的解释（略）

 用tf训练NN(部分）：

---

1.神经网络概述

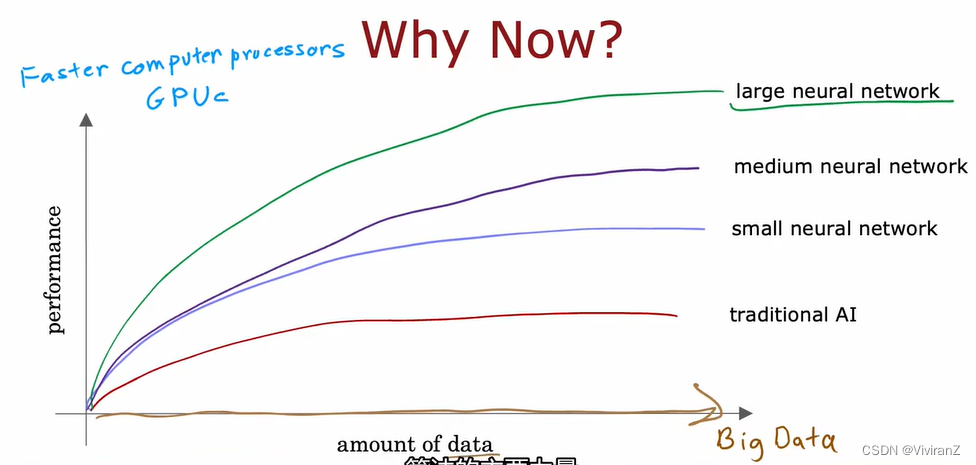
为什么近些年DL开始飞速发展？因为近年随着手机、电脑的发展，电子数据量飞速增长，而传统的AI模型(如之前的线性回归、逻辑斯蒂回归）的性能不够用了，也就是人类喂进去再多的数据，这些算法的性能也不会有太大的提高。因此，为了能更好利用数据，发展了NN。 

 一个单输入变量的简单例子：以T恤价格和是否销量高作为输入和输出，用logistics回归的公式，值得注意的是，我们用a替代原本回归模型中的f，这是因为在神经元中我们用激活（activate）表示这个函数启用了，所以为了统一此处用a。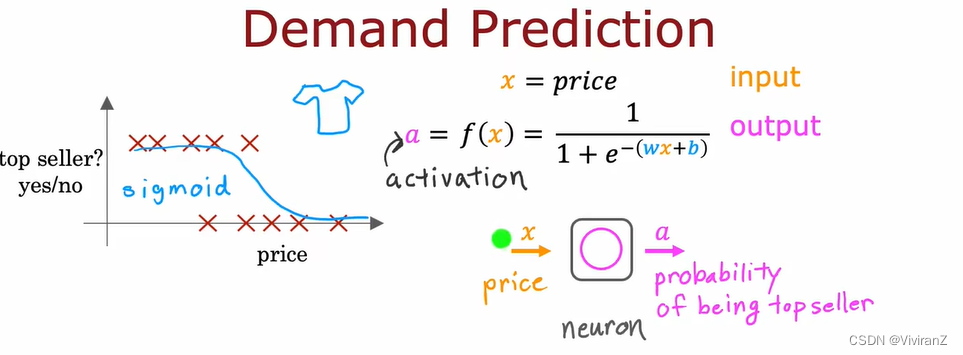

 接下来，以一个四维输入-一维输出为例构造一个三层的网络结构。

 也可以多个隐藏层，我们只需要确定需要多少层和每一层提取多少特征，然后电脑会帮我们提取合适的特征

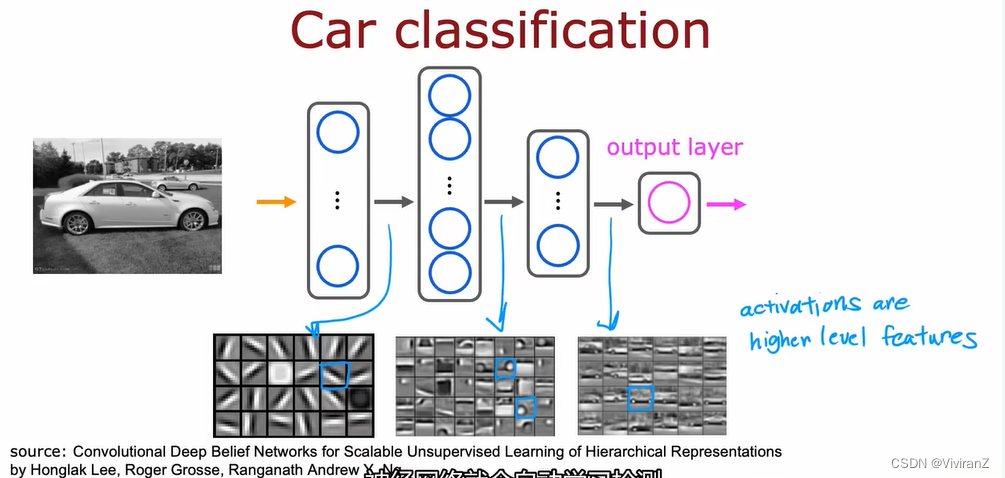
 一个人脸识别的例子：输入1000*1000像素的黑白照片，输出这个人是谁，那么对应NN的输入就是1000*1000维向量（如果RGB彩色图像那就是3million了）

随着层数加深，考虑的特征范围更广更宏观 

 细致写了一下一层的输出，每一层用上标[i]，每一层内部不同的神经元用下标1，也就是说，第一层的第二个神经元标识出来就是，对应参数是和

 同理，第一层的输出作为第二层的输入，其内部的表示如下图：

 最后，也可以增加一个predict category，也就是划为10（高维用one-hot)

 更复杂的NN（其实也很简单），注意，为了notation统一，输入X也可以被写成a_0

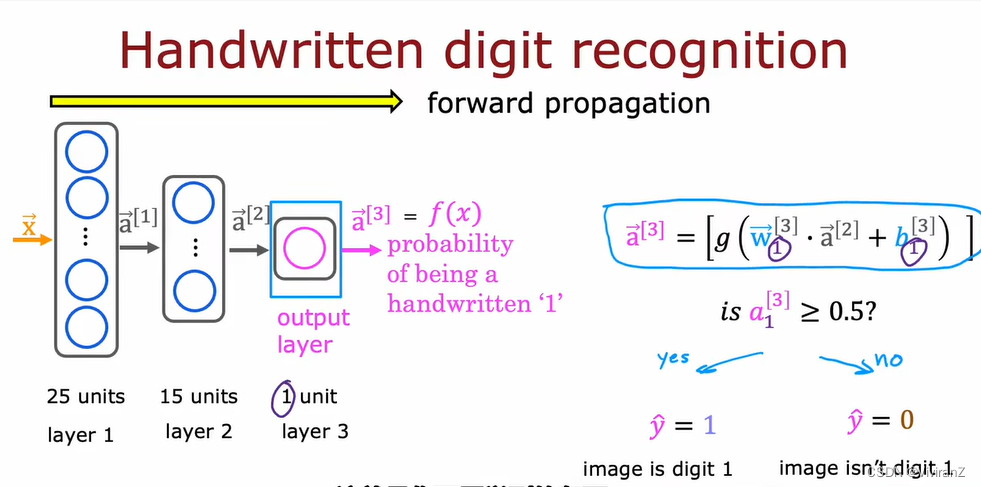
 以识别手写的01为例，其中0是黑色，255是亮白，两者之间是不同灰色

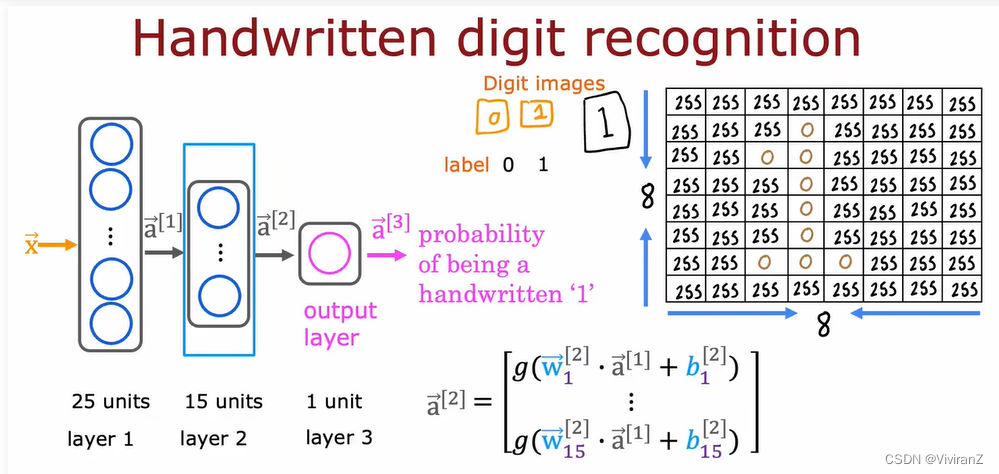
2 前向传播（forward propogation）神经网络

于是，我们学会了典型的前向传播的神经网络模型，

3. tensorflow实现

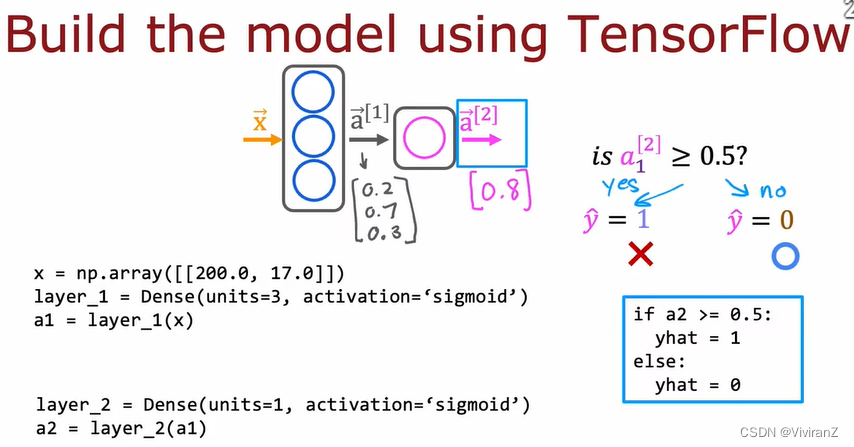
以咖啡烘焙是否出好豆子为例，输入是（烘焙温度，烘焙时间），输入是否为好豆子（是1否0）

我们考虑一个两层的神经网络，第一层有三个神经元、第二层有一个，都用sigmoid函数

 Numpy中的matrix：

这个我必须保存一波，天天记不得。

一重方括号表示的是向量vector，vector没有行列的概念，

二重方括号表示矩阵matrix，有行列

 代码显示如下：

 

我做了一个笔记

python中使用numpy包的向量矩阵相乘_ViviranZ的博客-CSDN博客

用循环写NN：

 如果完全用循环写，二层的NN是这样的：

（注意np.dot后面一个应该改为转置）

用numpy写NN:

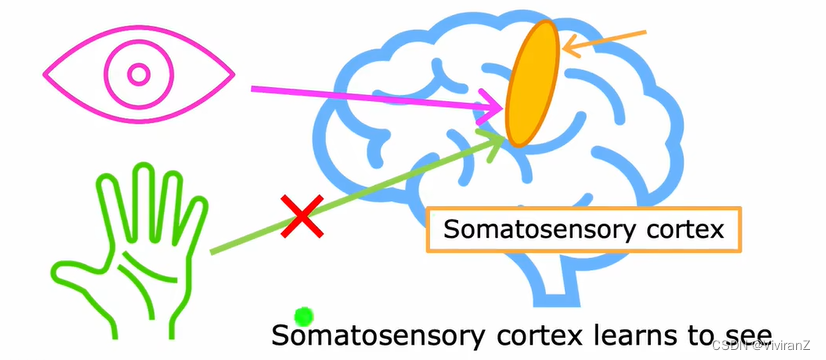
 AGI

 生物实验表明，同一块大脑的部分可能会有不同的功能。比如，生物学家切断了大脑一部分控制听觉的区域和耳朵的神经链接，转而给它图像信息，结果它学会看了。因此，AGI可能是可行的。

关于矩阵运算的解释（略）

神经网络模型的发展得益于利用矩阵乘法表示，在GPU和部分CPU中的函数非常擅长矩阵乘法的并行运算。

代码：

 两种不同的表示矩阵乘法的方式如上图，可以用np.matmul也可以直接用算符@。在这些基础上，就可以把NN进一步写成矩阵运算的形式（这样方便计算机进行并行计算）：

  np.dot和np.matmul在二维是一样的，具体笔记在博客附录：

python中使用numpy包的向量矩阵相乘np.dot和np.matmul_ViviranZ的博客-CSDN博客

 用tf训练NN：

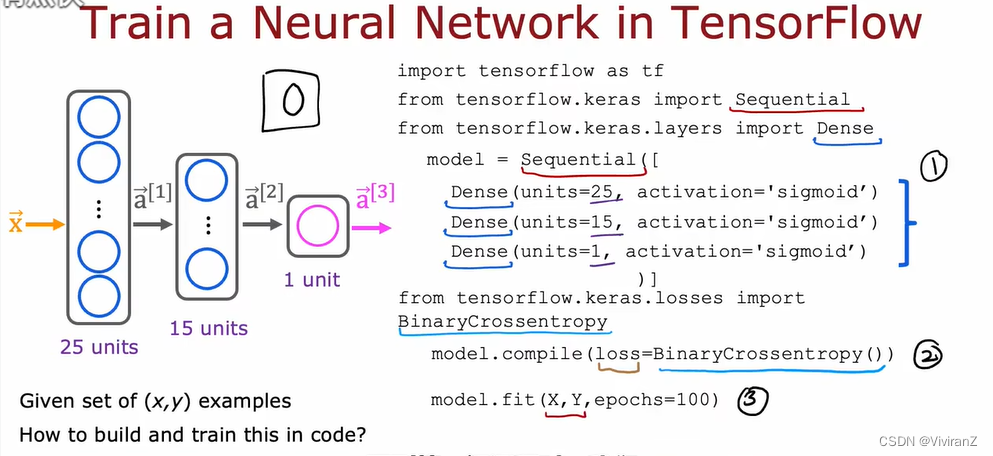
 epoch：对应第一课讲过的梯度下降法中，最多要走多少步。