14- 决策树算法 (有监督学习) (算法)

news2024/11/25 23:12:20

决策树是属于有监督机器学习的一种
决策树算法实操:

from sklearn.tree import DecisionTreeClassifier
# 决策树算法
model = DecisionTreeClassifier(criterion='entropy',max_depth=d)
model.fit(X_train,y_train)

1、决策树概述

决策树是属于有监督机器学习的一种，起源非常早，符合直觉并且非常直观，模仿人类做决策的过程，早期人工智能模型中有很多应用，现在更多的是使用基于决策树的一些集成学习的算法。这一章我们把决策树算法理解透彻了，非常有利于后面去学习集成学习。

1.1、示例一

上表根据历史数据，记录已有的用户是否可以偿还债务，以及相关的信息。通过该数据，构建的决策树如下：

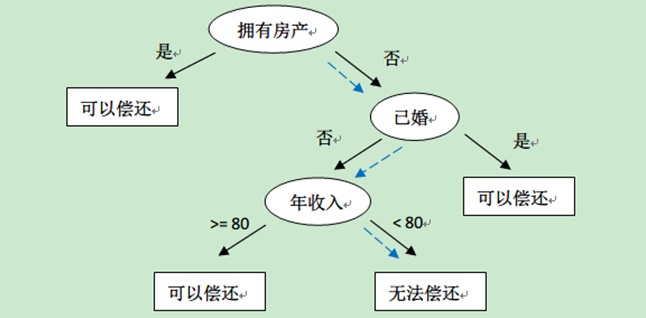
1.2、决策树算法特点

可以处理非线性的问题
可解释性强，没有方程系数
模型简单，模型预测效率高 if else

2、DecisionTreeClassifier使用

2.1、算例介绍

账号是否真实跟属性：日志密度、好友密度、是否使用真实头像有关系~

2.2、构建决策树并可视化

数据创建

import numpy as np
import pandas as pd
y = np.array(list('NYYYYYNYYN'))
print(y)
X = pd.DataFrame({'日志密度':list('sslmlmmlms'),
                  '好友密度':list('slmmmlsmss'),
                  '真实头像':list('NYYYYNYYYY'),
                  '真实用户':y})

数据调整

X['日志密度'] = X['日志密度'].map({'s':0,'m':1,'l':2})
X['好友密度'] = X['好友密度'].map({'s':0,'m':1,'l':2})
X['真实头像'] = X['真实头像'].map({'N':0,'Y':1})
X['真实用户'] = X['真实用户'].map({'N':0,'Y':1})

模型训练可视化

import matplotlib.pyplot as plt
from sklearn import tree
# 使用信息熵，作为分裂标准
model = DecisionTreeClassifier(criterion='entropy')
model.fit(X,y)
plt.rcParams['font.family'] = 'STKaiti'
plt.figure(figsize=(12,16))
fn = X.columns
_ = tree.plot_tree(model,filled = True,feature_names=fn)
plt.savefig('./iris.jpg')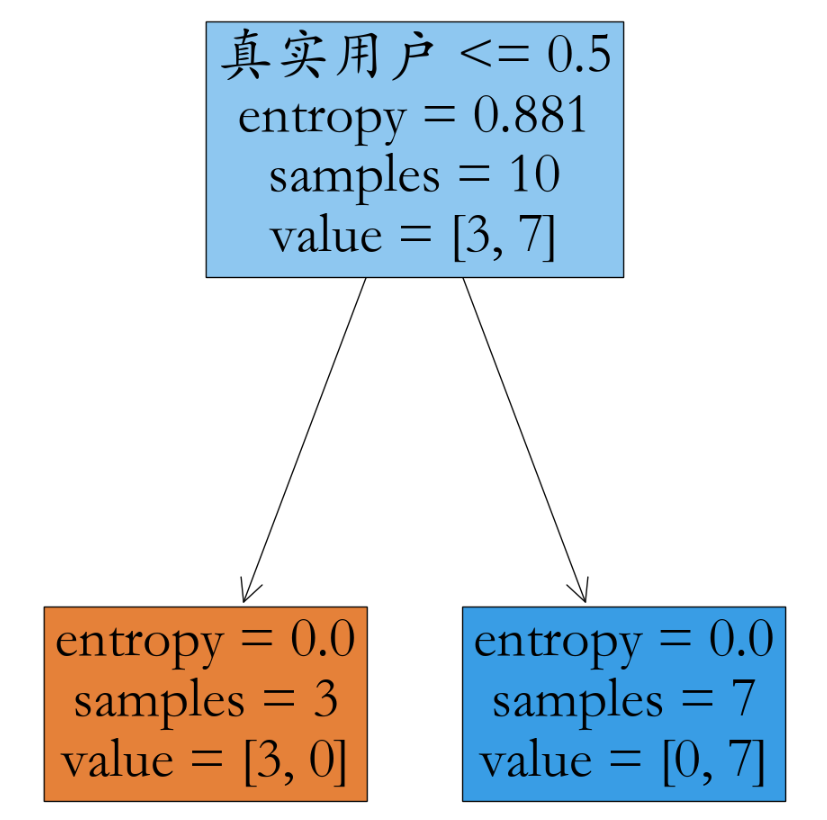

2.3、信息熵

构建好一颗树，数据变的有顺序了（构建前，一堆数据，杂乱无章；构建一颗，整整齐齐，顺序），用什么度量衡表示，数据是否有顺序：信息熵。
物理学，热力学第二定律（熵），描述的是封闭系统的混乱程度。

2.4、信息增益

信息增益是知道了某个条件后，事件的不确定性下降的程度。写作 g(X,Y)。它的计算方式为熵减去条件熵，如下:

$\bg_white \small g(X,y) \rm = H(Y) - H(Y|X)$

表示的是，知道了某个条件后，原来事件不确定性降低的幅度。

2.5、手动计算实现决策树分类

s = X['真实用户']
p = s.value_counts()/s.size
(p * np.log2(1/p)).sum()   # 0.8812908992306926

x = X['日志密度'].unique()
x.sort()
# 如何划分呢，分成两部分
for i in range(len(x) - 1):
    split = x[i:i+2].mean()
    cond = X['日志密度'] <= split
    # 概率分布
    p = cond.value_counts()/cond.size
    # 按照条件划分，两边的概率分布情况
    indexs =p.index
    entropy = 0
    for index in indexs:
        user = X[cond == index]['真实用户']
        p_user = user.value_counts()/user.size
        entropy += (p_user * np.log2(1/p_user)).sum() * p[index]
    print(split,entropy)

columns = ['日志密度','好友密度','真实头像']
lower_entropy = 1
condition = {}
for col in columns:
    x = X[col].unique()
    x.sort()
    print(x)
    # 如何划分呢，分成两部分
    for i in range(len(x) - 1):
        split = x[i:i+2].mean()
        cond = X[col] <= split
        # 概率分布
        p = cond.value_counts()/cond.size
        # 按照条件划分，两边的概率分布情况
        indexs =p.index
        entropy = 0
        for index in indexs:
            user = X[cond == index]['真实用户']
            p_user = user.value_counts()/user.size
            entropy += (p_user * np.log2(1/p_user)).sum() * p[index]
        print(col,split,entropy)
        if entropy < lower_entropy:
            condition.clear()
            lower_entropy = entropy
            condition[col] = split
print('最佳列分条件是：',condition)

3、决策树分裂指标

常用的分裂条件时：

信息增益
Gini系数
信息增益率
MSE（回归问题）

3.1、信息熵（ID3）

在信息论里熵叫作信息量，即熵是对不确定性的度量。从控制论的角度来看，应叫不确定性。信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。

对应公式:

$H(x) = -\sum\limits_{i = 1}^n p(x)log_2p(x)$

3.2、Gini系数（CART）

基尼系数是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。

基尼系数最大为“1”，最小等于“0”。基尼系数越接近 0 表明收入分配越是趋向平等。国际惯例把 0.2 以下视为收入绝对平均，0.2-0.3 视为收入比较平均；0.3-0.4 视为收入相对合理；0.4-0.5 视为收入差距较大，当基尼系数达到 0.5 以上时，则表示收入悬殊。

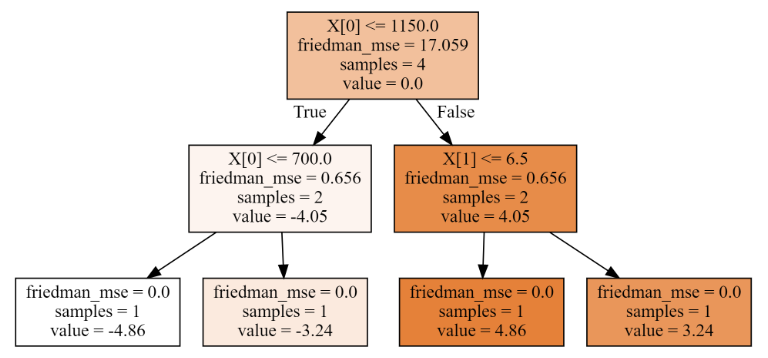
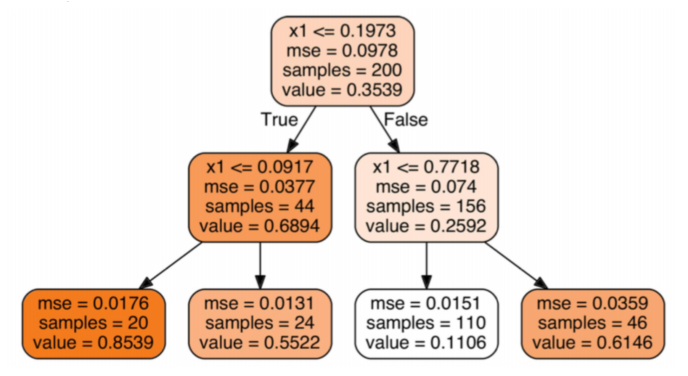
3.3、MSE

用于回归树，后面章节具体介绍

4、鸢尾花分类代码实战

4.1、决策树分类鸢尾花数据集

import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as plt

X,y = datasets.load_iris(return_X_y=True)

# 随机拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 256)

# max_depth调整树深度：剪枝操作
# max_depth默认，深度最大，延伸到将数据完全划分开为止。
model = DecisionTreeClassifier(max_depth=None,criterion='entropy')
model.fit(X_train,y_train)
y_ = model.predict(X_test)
print('真实类别是：',y_test)
print('算法预测是：',y_)
print('准确率是：',model.score(X_test,y_test))
# 决策树提供了predict_proba这个方法，发现这个方法，返回值要么是0，要么是1
model.predict_proba(X_test)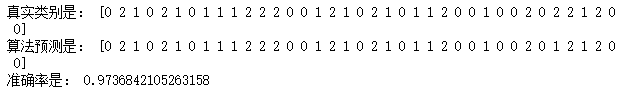

4.2、决策树可视化

import graphviz
from sklearn import tree
from sklearn import datasets
# 导出数据
iris = datasets.load_iris(return_X_y=False)
dot_data = tree.export_graphviz(model,feature_names=fn,
                     class_names=iris['target_names'],# 类别名
                     filled=True, # 填充颜色
                     rounded=True,)
graph = graphviz.Source(dot_data)
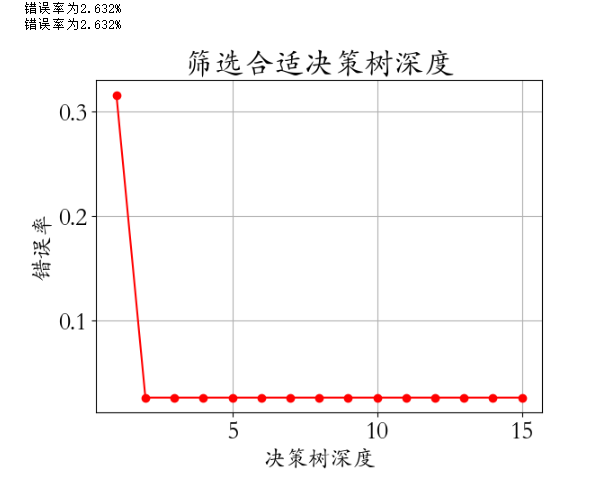
graph.render('iris')

4.3、选择合适的超参数并可视化

import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import tree
import matplotlib.pyplot as plt

X,y = datasets.load_iris(return_X_y=True)

# 随机拆分
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 256)
depth = np.arange(1,16)
err = []
for d in depth:
    model = DecisionTreeClassifier(criterion='entropy',max_depth=d)
    model.fit(X_train,y_train)
    score = model.score(X_test,y_test)
    err.append(1 - score)
    print('错误率为%0.3f%%' % (100 * (1 - score)))
plt.rcParams['font.family'] = 'STKaiti'
plt.plot(depth,err,'ro-')
plt.xlabel('决策树深度',fontsize = 18)
plt.ylabel('错误率',fontsize = 18)
plt.title('筛选合适决策树深度')
plt.grid()
plt.savefig('./14-筛选超参数.png',dpi = 200)