note

• node2vec：
  • 计算随机游走概率
  • 从节点$u$开始模拟$r$条长度为$l$的游走链路
  • 使用 Stochastic Gradient Descent 优化损失函数
• Node2vec在节点分类方面表现更好；而其他方法在链路预测上效果更好，如random walk效率更高；
• graph embeddings：
  • 方法1：对应子图or图的节点embedding进行sum或avg计算；
  • 方法2：创建横跨子图的super-node
• deepwalk等价于对以下表达式进行矩阵分解：$$\log \left(\mathrm{vol}(G)\left(\frac{1}{T}\sum _{r=1}^T{\left(D^{-1}A\right)}^r\right)D^{-1}\right)-\log b$$
  

一、Node embedding: Encoder + Decoder

本讲是图表示学习综述，介绍了图嵌入（节点嵌入）表示学习的基本框架和编码器-解码器架构，将节点嵌入映射为低维、连续、稠密向量。向量空间的相似度反映了对应节点在原图上的相似度。在同一个随机游走序列中共同出现的节点，视为相似节点，从而构建类似Word2Vec的自监督学习场景。衍生出DeepWalk、Node2Vec等基于随机游走的图嵌入方法。

从数学上，随机游走方法和矩阵分解是等价的。

进而讨论嵌入整张图的方法，可以通过所有节点嵌入向量聚合、引入虚拟节点、匿名随机游走等方法实现。

• embedding编码网络中的信息，可用于下游任务， 图表示学习使得省去特征工程。
  
• 图$G$，节点集$V$，邻接矩阵$A$（二维，这里化简，不考虑节点的特征等信息）
• node embedding：将节点信息编码为space中的embedding，使得embedding的相似度计算（如cos点积计算等）近似于节点之间真实的相似度

1.1 embedding-lookup

• 注意两点：
  
• shallow encoding：encoder仅为embedding-lookup表$$\mathrm{ENC}(v)={\mathbf{z}}_v=\mathbf{Z}\cdot v$$
  • $\mathbf{Z}\in {\mathbb{R}}^{d\times |\mathcal{V}|}$矩阵中，每列是对应的节点的embedding
  • $v\in {\mathbb{I}}^{|\mathcal{V}|}$ 是单位矩阵
  • 方法：deepwalk、node2vec等
  • goal：对于相似节点(u, v)，优化参数，使得$$\mathrm{similarity}(u,v)\approx {\mathbf{z}}_v^{\mathrm{T}}{\mathbf{z}}_u$$

1.2 节点相似的定义

• 有边
• 共享邻居
• 有相似的structural roles
• 随机游走random walk定义的节点相似度

1.3 unsupervised/self-supervised

无监督or自监督学习：不使用节点的标签和特征，直接得到节点的度量（如embedding）

二、Random Walk

2.1 notation

• ${\mathbf{z}}_u$：我们想学习到的节点u embedding
• $P\left(v\mid {\mathbf{z}}_u\right)$条件概率：已知节点u embedding，基于random walk的要访问节点v的概率
• 通过非线性函数得到预测概率：
  • softmax函数将数据归一化为和为1的结果：$$\sigma (\mathbf{z})[i]=\frac{e^{z[i]}}{{\sum }_{j=1}^K{e}^{z[j]}}$$
  • sigmoid函数：转为(0, 1)范围内，公式为$$S(x)=\frac{1}{1+e^{-x}}$$

2.2 Algorithm:DeepWalk

算法由两部分组成：

• （1）随机游走序列生成器；
• （2）向量更新。

随机游走：对图G均匀地随机采样一个节点$v_i$，并作为random walk的根结点$W_{v_i}$，然后一直向周围邻居采样，直到达到最大路径长度$t$。
随机游走的长度没有限制，但是在实验中设置最大步长是固定的。

• 输出：一个顶点表示矩阵$\Phi$，大小为$|V|\times d$
• 第二行：构建Hierarchical Softmax
• 第三行：对每个节点做$\gamma$次随机游走
• 第四行：打乱网络中的节点
• 第五行：以每个节点为根结点生成长度为$t$的随机游走
• 第七行：根据生成的随机游走使用skip-gram模型利用梯度的方法对参数进行更新。

其中SkipGram参数更新的细节如下：

（1）SkipGram

SkipGram参数更新的细节如下：

SkipGram算法是语言模型中，最大化窗口$w$中出现的词的概率的方法（梯度下降），外层for循环是对这个序列中的每个词进行操作，内层for循环是对每个词的窗口大小为$w$的词序列进行操作。具体操作是用一个似然函数$J(\Phi )$表示$\Phi$，通过梯度下降（对$J(\Phi )$求导）更新参数（$\alpha$是学习速率）。

从词向量学习的角度看，基于神经网络语言模型的预训练方法存在缺点：当对t时刻词进行预测时，模型只利用了历史词序列作为输入，而损失了与“未来”上下文之间的共现信息。于是大佬们提出更强的词向量预训练模型Word2Vec，其中包括CBOW(Continuous Bag-of-Words)模型以及Skip-gram模型。

（2）Hierarchical Softmax

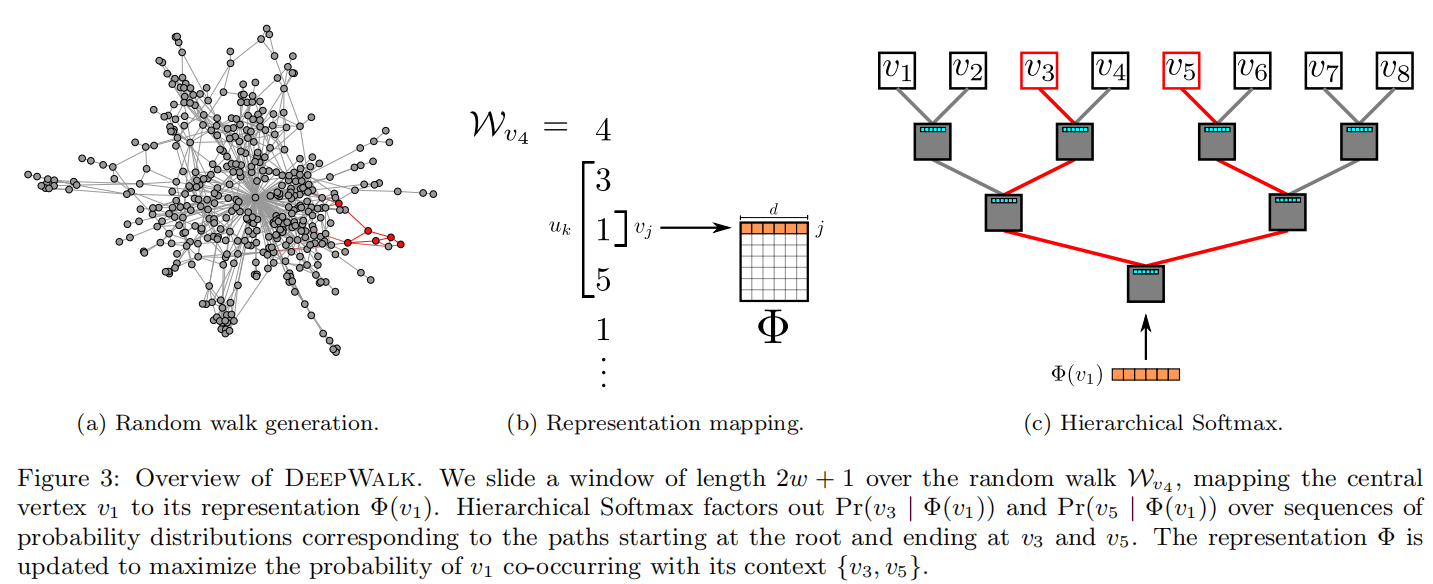
在计算 $\mathrm{Pr}(u_k|\Phi (v_i))$ 时，可以利用Hierarchical Softmax二叉树[29, 30]加速。作者将所有节点作为二叉树的叶子节点，就可以用从根节点到叶子节点的路径来表示每个节点。二叉树若有$|V|$个叶子节点，则深度至多为$\log |V|$。这样就会有：
$$\mathrm{Pr}(u_k|\Phi (v_j))=\prod _{l=1}^{\lceil \log |V|\rceil }\mathrm{Pr}(b_l|\Phi (v_j))$$其中$b_0,b_1,...,b_{\lceil \log |V|\rceil }$是一系列二叉树中的非叶子节点。这样就可以用较少的分类器完成这个任务，将计算复杂度由$O(|V|)$降低至$O(\log |V|)$。

更进一步，还可以结合节点出现频率，使用霍夫曼编码，为更频繁出现的节点分配稍短的路径，再次降低计算复杂度。

（3）Optimization

模型参数集是 { Φ , T } \{\Phi, T\} {Φ,T}，使用随机梯度下降算法 $SGD$（一次训练一个样本）进行优化参数。通过方向传播计算损失函数关于参数的偏导数，SGD的学习率初始设置为2.5%，然后随着训练过程中看到的顶点数量的增加而线性减少。

• 目标：使对每个节点 $u,N_R(u)$ 的节点和 $z_u$ 靠近, 即 $P\left(N_R(u)\mid z_u\right)$ 值大。
• $\mathrm{f}:\mathrm{u}\to {\mathbb{R}}^{\mathrm{d}}:\mathrm{f}(\mathrm{u})={\mathbf{z}}_{\mathrm{u}}$。
• 优化embedding的log-likelihood目标函数：
  $$\underset{f}{\max }\sum _{u\in V}\log \mathrm{P}\left(N_{\mathrm{R}}(u)\mid {\mathbf{z}}_u\right)$$
  
  【负采样优化】
  但是由于求解上面目标函数的时间复杂度很高，需要$\mathrm{O}\left(|\mathrm{V}{|}^2\right)$，可以通过负采样优化该公式的分母，即不用所有节点作为归一化的负样本。
  

2.3 代码实战

# DiGraph with 100 nodes and 4961 edges
import networkx as nx
import numpy as np
from tqdm import tqdm
from gensim.models import word2vec

def walkOneTime(g, start_node, walk_length):
    walk = [str(start_node)]  # 初始化游走序列
    for _ in range(walk_length):  # 最大长度范围内进行采样
        current_node = int(walk[-1])
        successors = list(g.successors(current_node)) # graph.successor: 获取当前节点的后继邻居
        if len(successors) > 0:
            next_node = np.random.choice(successors, 1)
            walk.extend([str(n) for n in next_node])
        else:
            break
    return walk

def getDeepwalkSeqs(g, walk_length, num_walks):
    seqs=[]
    for _ in tqdm(range(num_walks)):
        start_node = np.random.choice(g.nodes)
        w = walkOneTime(g,start_node, walk_length)
        seqs.append(w)
    return seqs

def deepwalk( g, dimensions = 10, walk_length = 80, num_walks = 10, min_count = 3 ):
    seqs = getDeepwalkSeqs(g, walk_length = walk_length, num_walks = num_walks)
    model = word2vec.Word2Vec(seqs, vector_size = dimensions, min_count = min_count)
    return model

if __name__ == '__main__':
	#快速随机生成一个有向图
    g = nx.fast_gnp_random_graph(n = 100, p = 0.5,directed = True) 
    model = deepwalk( g, dimensions = 10, walk_length = 20, num_walks = 100, min_count = 3 )
    # 观察与节点2最相近的三个节点
    print(model.wv.most_similar('2',topn=3))
    # 可以把emd储存下来以便下游任务使用
    model.wv.save_word2vec_format('e.emd')
    # 可以把模型储存下来以便下游任务使用
    model.save('m.model')

• 先利用networkx随机生成二项式有向图（如下图所示）
• walk_length是每条random walk链路的长度，共有num_walks条链路，通过随机游走得到的seqs送入到gensim.models.word2vec中训练w2v，保存训练得到的embedding和模型m.model。
• 得到与节点2最接近的3个节点：[('77', 0.8721016049385071), ('65', 0.8555149435997009), ('66', 0.8495140671730042)]。

2.4 小结

三、在同质性和结构性间权衡：Node2vec

2016 年，斯坦福大学大佬在 DeepWalk 的基础上提出了 Node2vec 模型。Node2vec 通过调整随机游走跳转概率的方法，让 Graph Embedding 的结果在网络的同质性（Homophily）和结构性（Structural Equivalence）中进行权衡，可以进一步把不同的 Embedding 输入推荐模型，让推荐系统学习到不同的网络结构特点。

3.1 同质性和结构性

网络的“同质性”指的是距离相近节点的 Embedding 应该尽量近似，如图 3 所示，节点 u 与其相连的节点 s1、s2、s3、s4的 Embedding 表达应该是接近的，这就是网络“同质性”的体现。在电商网站中，同质性的物品很可能是同品类、同属性，或者经常被一同购买的物品。

“结构性”指的是结构上相似的节点的 Embedding 应该尽量接近，比如图 3 中节点 u 和节点 s6都是各自局域网络的中心节点，它们在结构上相似，所以它们的 Embedding 表达也应该近似，这就是“结构性”的体现。在电商网站中，结构性相似的物品一般是各品类的爆款、最佳凑单商品等拥有类似趋势或者结构性属性的物品。

图3 网络的BFS和DFS示意图

3.2 如何表达结构性和同质性

Graph Embedding 的结果究竟是怎么表达结构性和同质性的呢？

• 首先，为了使 Graph Embedding 的结果能够表达网络的“结构性”，在随机游走的过程中，我们需要让游走的过程更倾向于 BFS（Breadth First Search，宽度优先搜索），因为 BFS 会更多地在当前节点的邻域中进行游走遍历，相当于对当前节点周边的网络结构进行一次“微观扫描”。（当前节点是“局部中心节点”，还是“边缘节点”，亦或是“连接性节点”，其生成的序列包含的节点数量和顺序必然是不同的，从而让最终的 Embedding 抓取到更多结构性信息。）

• 而为了表达“同质性”，随机游走要更倾向于 DFS（Depth First Search，深度优先搜索）才行，因为 DFS 更有可能通过多次跳转，游走到远方的节点上。但无论怎样，DFS 的游走更大概率会在一个大的集团内部进行，这就使得一个集团或者社区内部节点的 Embedding 更为相似，从而更多地表达网络的“同质性”。

那在 Node2vec 算法中，究竟是怎样控制 BFS 和 DFS 的倾向性的呢？

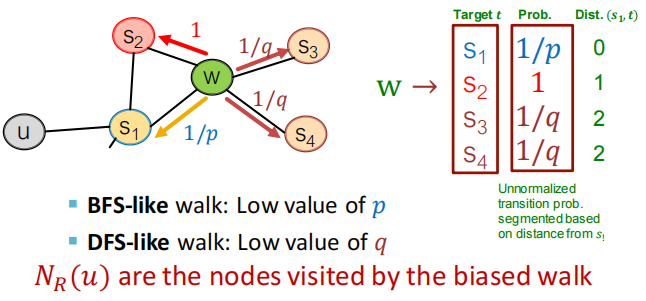
• 其实，它主要是通过节点间的跳转概率来控制跳转的倾向性。图 4 所示为 Node2vec 算法从节点 t 跳转到节点 v 后，再从节点 v 跳转到周围各点的跳转概率。这里，你要注意这几个节点的特点。比如，节点 t 是随机游走上一步访问的节点，节点 v 是当前访问的节点，节点 x1、x2、x3是与 v 相连的非 t 节点，但节点 x1还与节点 t 相连，这些不同的特点决定了随机游走时下一次跳转的概率。

图4 Node2vec的跳转概率

这些概率还可以用具体的公式来表示，从当前节点 v 跳转到下一个节点 x 的概率$${\pi }_{vx}={\alpha }_{pq}(t,x)\cdot {\omega }_{vx}$$其中 Wvx 是边 vx 的原始权重，${\alpha }_{pq}(t,x)$ 是 Node2vec 定义的一个跳转权重。到底是倾向于 DFS 还是 BFS，主要就与这个跳转权重的定义有关了：

$${\alpha }_{pq(t,x)=}\{\begin{array}{ll}\frac{1}{p}& \text{ 如果 }{d}_{tx}=0\\ 1& \text{ 如果 }{d}_{tx}=1\\ \frac{1}{q}& \text{ 如果 }{d}_{tx}=2\end{array}$$

${\alpha }_{pq}(t,x)$里的$d_{tx}$ 是指节点 t 到节点 x 的距离，比如节点 x1其实是与节点 t 直接相连的，所以这个距离 $d_{tx}$就是 1，节点 t 到节点 t 自己的距离 $d_{tt}$就是 0，而 x2、x3这些不与 t 相连的节点，$d_{tx}$就是 2。

此外，${\alpha }_{pq}(t,x)$ 中的参数 p 和 q 共同控制着随机游走的倾向性。参数 p 被称为返回参数（Return Parameter），p 越小，随机游走回节点 t 的可能性越大，Node2vec 就更注重表达网络的结构性。参数 q 被称为进出参数（In-out Parameter），q 越小，随机游走到远方节点的可能性越大，Node2vec 更注重表达网络的同质性。

反之，当前节点更可能在附近节点游走。可以自己尝试给 p 和 q 设置不同大小的值，算一算从 v 跳转到 t、x1、x2和 x3的跳转概率。这样应该就能理解刚才所说的随机游走倾向性的问题啦。

3.3 实验证实+代码例子

Node2vec 这种灵活表达同质性和结构性的特点也得到了实验的证实，可以通过调整 p 和 q 参数让它产生不同的 Embedding 结果。

• 图 5 上就是 Node2vec 更注重同质性的体现，从中可以看到，距离相近的节点颜色更为接近；
• 图 5 下则是更注重结构性的体现，其中结构特点相近的节点的颜色更为接近。

图5 Node2vec实验结果

Node2vec 所体现的网络的同质性和结构性，在推荐系统中都是非常重要的特征表达。由于 Node2vec 的这种灵活性，以及发掘不同图特征的能力，可以把不同 Node2vec 生成的偏向“结构性”的 Embedding 结果，以及偏向“同质性”的 Embedding 结果共同输入后续深度学习网络，以保留物品的不同图特征信息。

【代码例子】通过Node2vec找到和节点2最接近的3个节点

import networkx as nx
from node2vec import Node2Vec

graph = nx.fast_gnp_random_graph(n=100, p=0.5)#快速随机生成一个无向图
node2vec = Node2Vec ( graph, dimensions=64, walk_length=30, num_walks=100, p=0.3,q=0.7,workers=4)#初始化模型
model = node2vec.fit()#训练模型
print(model.wv.most_similar('2',topn=3))# 观察与节点2最相近的三个节点
'''
[('43', 0.5867125988006592), ('41', 0.5798742175102234), ('33', 0.5246706008911133)]
'''

四、Embedding Entire Graphs

4.1 得到子图或整图的embedding

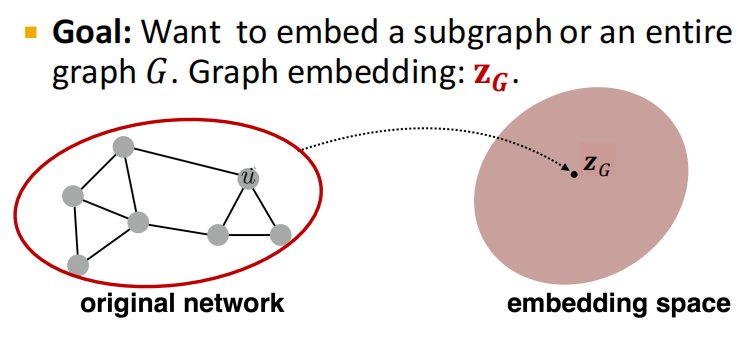
4.2 anonymous walks的应用

4.3 小结

附：思考题

机器学习中的“表示学习”是做什么的？为什么要做表示学习？

CS224W整门课程，都对哪些研究对象进行了嵌入编码的表示学习操作？

图嵌入有什么用？

图嵌入有哪几种技术方案？各有什么优劣？

如何理解图嵌入向量的“低维、连续、稠密”

如何衡量两个节点是否“相似”？

图嵌入中，Decoder为什么用两个向量的数量积？

如何理解图嵌入中的Shallow Encoder和Deep Encoder？有何区别？

随机游走序列包含了哪些信息？

图机器学习和自然语言处理存在怎样的对应关系？

简述DeepWalk算法原理

简述Node2Vec算法原理

除了DeepWalk和Node2Vec之外，还有哪些基于随机游走的图嵌入算法？

同济子豪兄论文精读视频中，DeepWalk和Node2Vec也留了不少思考题，去看看吧

你是否能想出更科学的随机游走策略？

基于随机游走的图嵌入方法，都可以被统一成什么样的数学形式？

重新思考：为什么要把图表示成矩阵的形式？

附：时间安排

任务	任务内容	截止时间	注意事项
	2月11日开始
task1	图机器学习导论	2月14日周二	完成
task2	图的表示和特征工程	2月15、16日周四	完成
task3	NetworkX工具包实践	2月17、18日周六	完成
task4	图嵌入表示	2月19、20日周一	完成
task5	deepwalk、Node2vec论文精读	2月21、22日周三
task6	PageRank	2月23、24日周五
task7	标签传播与节点分类	2月25、26日周日
task8	图神经网络基础	2月27、28日周二
task9	图神经网络的表示能力	3月1日周三
task10	图卷积神经网络GCN	3月2日周四
task11	图神经网络GraphSAGE	3月3日周五
task12	图神经网络GAT	3月4日周六

Reference

[1] 传统图机器学习的特征工程-节点【斯坦福CS224W】
[2] cs224w（图机器学习）2021冬季课程学习笔记2: Traditional Methods for ML on Graphs
[3] NetworkX入门教程
[4] https://github.com/TommyZihao/zihao_course/tree/main/CS224W
[5] 斯坦福官方课程：https://web.stanford.edu/class/cs224w/
[6] 子豪兄github：https://github.com/TommyZihao/zihao_course
[7] 子豪：随机游走的艺术-图嵌入表示学习【斯坦福CS224W图机器学习】
[8] Graph Embedding-Node2vec总结
[9] nx.draw报错 ‘_AxesStack‘ object is not callable
[10] Embedding技术在推荐系统中的应用
[11] cs224w（图机器学习）2021冬季课程学习笔记3: Node Embeddings
[12] networkx官方文档：fast_gnp_random_graph