1.题目链接:139. 单词拆分
题目描述:
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
解法:
1.五步曲:
①将其转化为背包问题就是给定容量为s.size()的背包,问能不能把它装满。
②dp[j]表示的就是根据wordDict字典能否填满容量为j的背包,能的话dp[j] = true;不能的话就是false。
③递推公式:dp[j] = ? 假设一段上要求dp[j],那么在j之前有个位置i,当dp[i] = true且字典中包含从i到j-1的位置的字符串。这样dp[j] = true;故 if(dp[i] == true && set.contains(substring(i,j))){dp[j] = true;}
④初始化:因为根据递推公式,当前值是根据前面的值得到,所以初始化dp[0] = true --- 可以这样理解,即如果容量为0,根据字典不填东西,就能填满这个背包,所以是true。非0位置初始化为false,因为一开始不知道是否能拼出s,所以初始值应该为false。
⑤遍历顺序:首先单词可以重复使用,所以完全背包问题,背包正序遍历。然后假如s = applepenapple,字典中有apple,pen两个元素。那么将其组合成s要求121,112就不行,所以对顺序有要求,故求排列数,故先遍历背包再遍历物品。
⑥最后返回dp[s.size()]
⑦Note:因为我要判断字典中是否包含从i到j-1位置的字符串,所以要用到contains方法,所以要将给定的链表转成HashSet,这样就能用contains方法了。截取字符串用substring(i,j)左闭右开。
⑧在遍历物品的时候终止条件是i < j,因为分析递推公式的时候,i就是小于j的。同时也可以这样想,递推公式里的判断就要求i<j,否则set.contains(substring(i,j))就错误了。
2.步骤:
①创建dp数组,长度为s.size()+1
②将字典转化成集合--- 即HashSet<String> set = new ArrayList<>(wordDict)
③初始化:dp[0] = true;其余位置在创建数组的时候相当于自动初始化成false了。
④遍历顺序:for(int j = 1;j <= s.size();j++){
for(int i = 0; i < j;i++){
if(dp[i] == true && set.contains(substring(i,j) ){
dp[j] = true;
}
}
}
⑤最后返回dp[s.size()]
下面为代码(java):

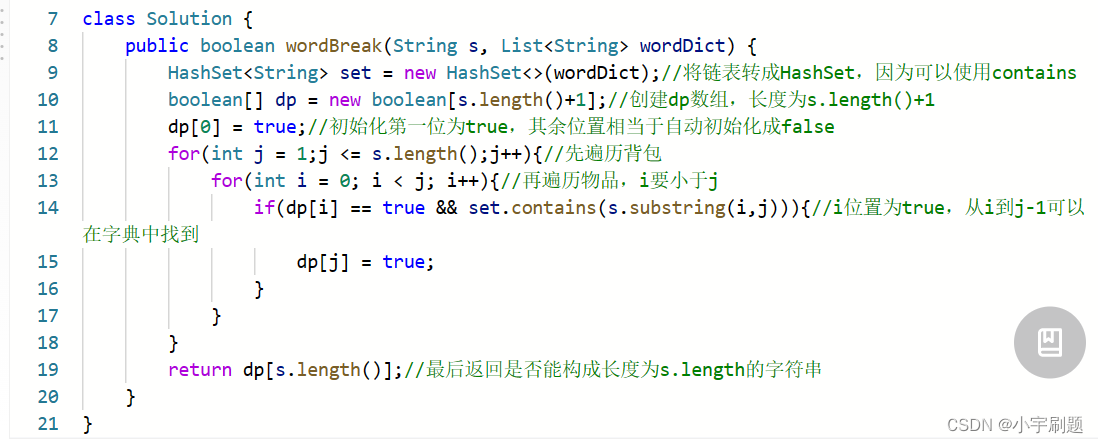
2.题目链接: 多重背包
题目描述:
给定一个容量为bagSize的背包,给定一堆物品,第i个物品对应重量为weight[i],价值为value[i],物品个数为nums[i],求装满背包的最大价值为多少?
解法:
1.五步曲:
①其实看起来很像01背包问题,不同之处就是01背包每个物品只能用一次,而这里每个物品都有个数,那么将个数摊开就变成了01背包问题。
②如何摊开:
1)首先我们将weight,value,nums数组都转成链表格式 = new ArrayList<>(Arrays.asList(1,3,5));
2)while(nums.get(i) > 1){// 即有多的weight里加一个,value里加一个,重新设置nums链表第i个位置的值
weight.add(weight.get(i));
value.add(value.get(i));
nums.set(i,nums.get(i) - 1); --- 重新设置nums链表中第i个位置的值
}
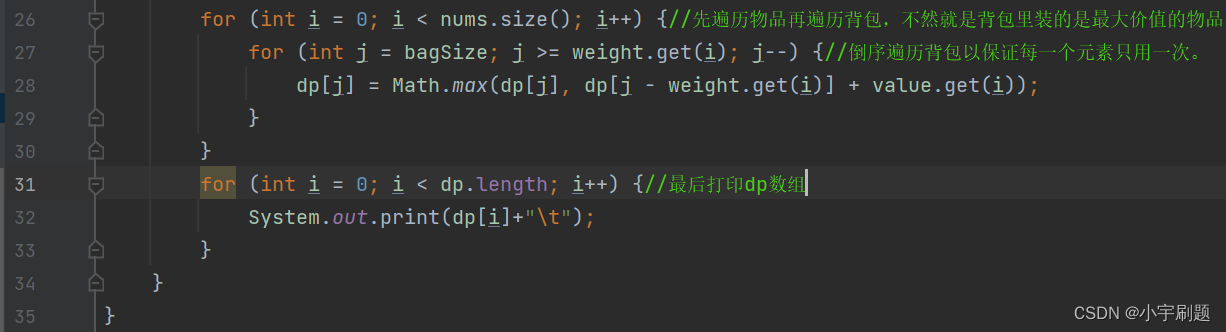
③这样就变成了01背包 --- 递推公式:即dp[j] = max(dp[j] , dp[j-weight[i]] + value[i]);遍历顺序:倒序背包(保证每一个物品只用一次);先物品后背包(不然的话求的就是每个背包中装价值最大的物品)。
2.步骤:
①List<Integer> weight = new ArrayList<>(Arrays.asList(1,3,5))
②再分别创建value和nums
③然后将多重背包变成01背包问题,即摊开
for(int i = 0; i < nums.length ;i++){
while(nums.get(i) > 1){
weight.add(weight.get(i));
value.add(value.get(i));
nums.set(i, nums.get(i) - 1);//即nums中i位置的值减减
}
}
④剩下就是01背包的创建dp数组,确定递推公式,初始化,确定遍历顺序,最后返回dp[bagSize]。
下面为代码(java):
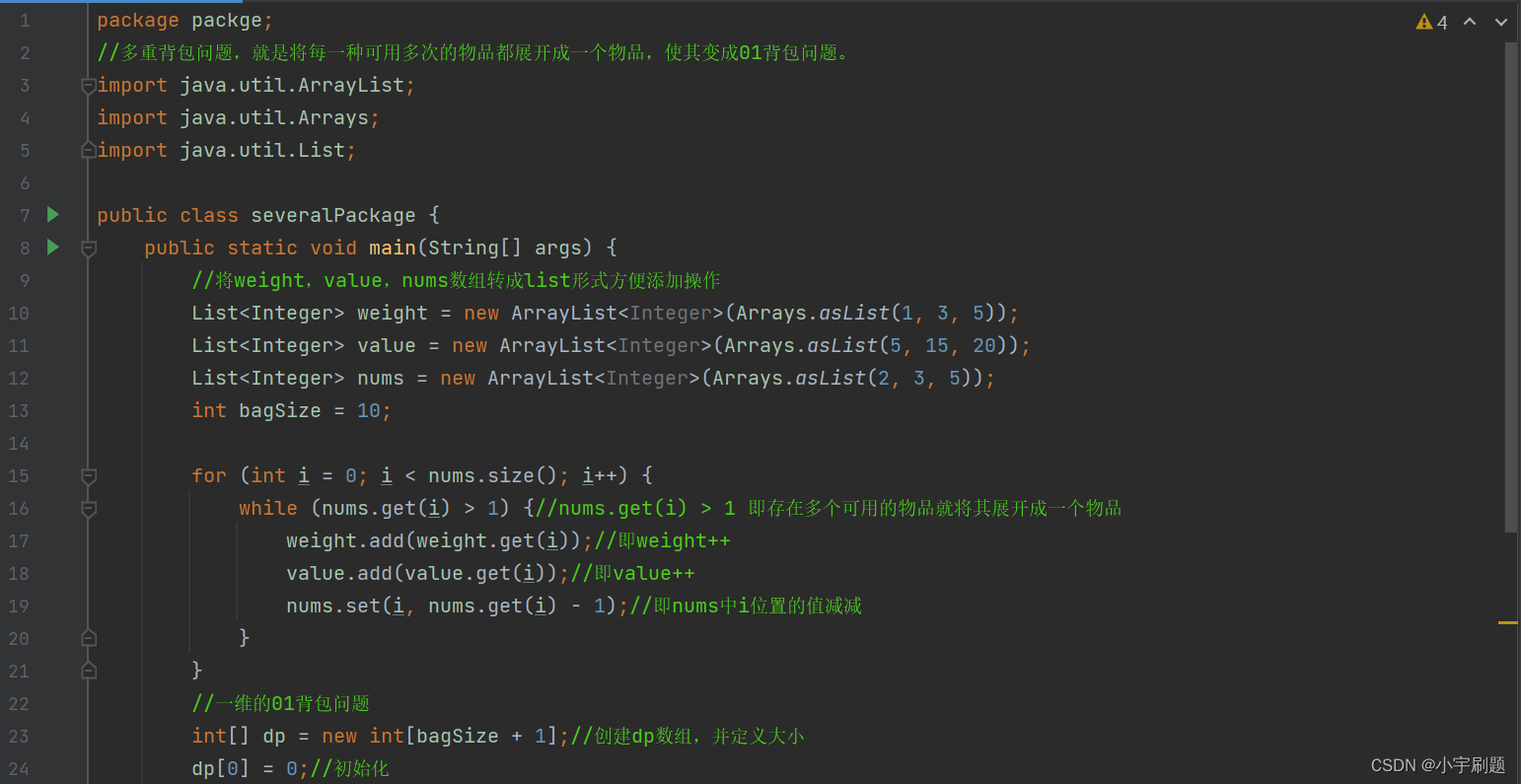
 3.总结:
3.总结:
①单词拆分问题:
1)dp[j]代表能否根据字典填充满长度为j的字符串。
2)递推公式要根据前面的i位置的状态以及i到j-1是否能在字典中找到判断。
3)遍历顺序:字典单词可用多次---完全背包;要求结果有顺序---排列数,先背包后物品。
4)初始化:dp[0] = true,非0为false。
②多重背包问题:将其的物品个数摊开,就变成了01背包。