15- 决策回归树, 随机森林, 极限森林 (决策树优化) (算法)

news2024/11/26 4:51:57
  • 1.  决策回归树:
from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor(criterion='mse',max_depth=3)
model.fit(X,y)    # X是40个点 y是一个圆
  • 2.  随机森林 + 稳定预测:
from sklearn.ensemble import RandomForestClassifier
# model = RandomForestClassifier()
# model.fit(X_train,y_train)
score = 0
for i in range(100):
    model = RandomForestClassifier()
    model.fit(X_train,y_train)
    score += model.score(X_test,y_test)/100
print('随机森林平均准确率是：',score)
  • 3. 极限森林:
from sklearn.ensemble import ExtraTreesClassifier
clf3 = ExtraTreesClassifier(max_depth = 3)
clf3.fit(X_train,y_train)

1、决策回归树原理概述

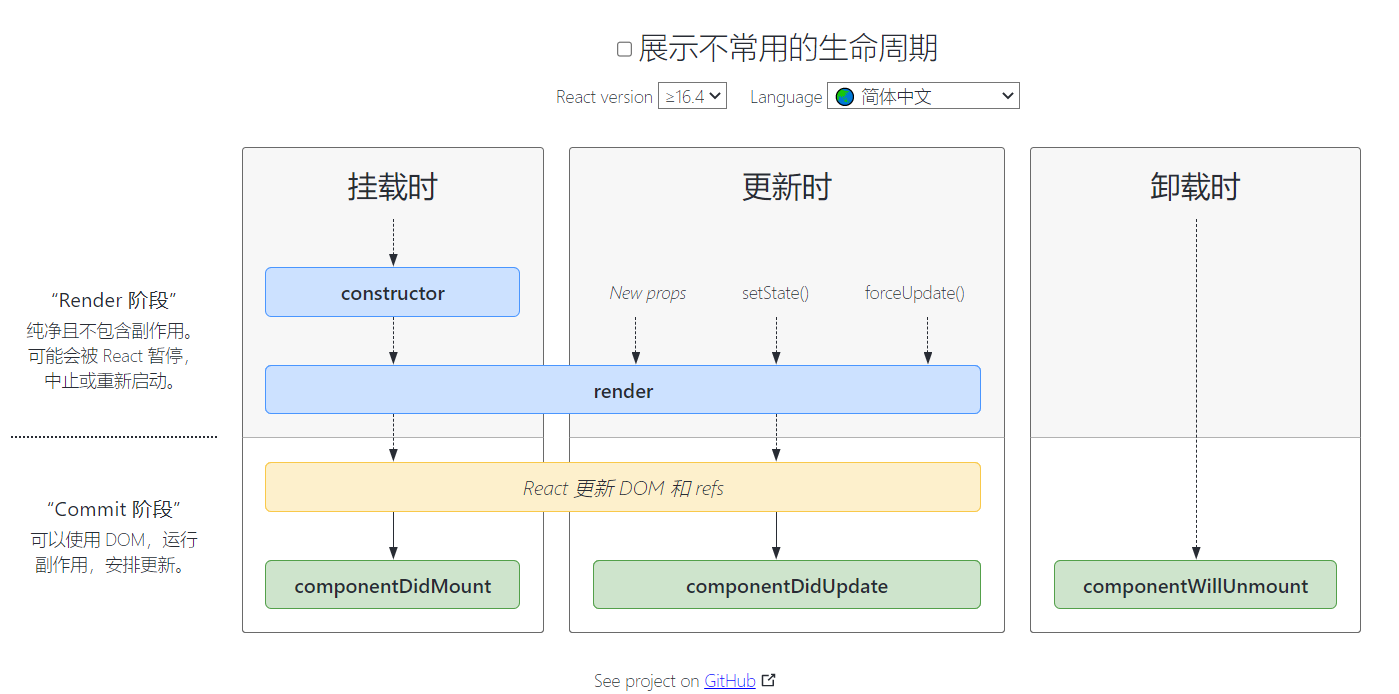
  • 与分类树一样

  • 裂分指标，使用的是MSE、MAE

        \bg_white \small \text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum\limits_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2

        \text{MAE}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum\limits_{i=0}^{n_{\text{samples}}-1} \left| y_i - \hat{y}_i \right|

  • 决策回归树，认为它是分类问题，只是，分的类别多一些！！！

  • 只要树，分类回归，其实就是分类多和少的问题

2、决策回归树算例

2.1、决策树预测圆的轨迹

2.1.1 导包并创建数据与可视化 

import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import graphviz
X = np.linspace(0,2*np.pi,40).reshape(-1,1)
X_test = np.linspace(0,2*np.pi,187).reshape(-1,1)
# y 一个正弦波，余弦波，圆
y = np.c_[np.sin(X),np.cos(X)]
plt.figure(figsize=(3,3))
plt.scatter(y[:,0],y[:,1])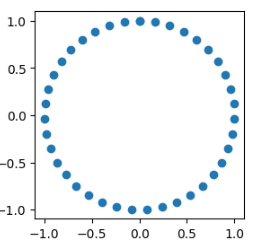

2.1.2 使用线性回归预测，看效果 

linear = LinearRegression()
linear.fit(X,y) #将数据交给算法，学习，希望算法，找到规律
# X ----> y 是一个圆；预测X_test返回值y_ 如果预测好，也是圆
y_ = linear.predict(X_test)
plt.figure(figsize=(3,3))
plt.scatter(y_[:,0],y_[:,1])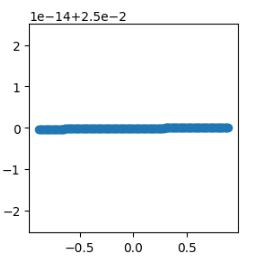

 2.1.3 使用决策树回归，看效果 

model = DecisionTreeRegressor(criterion='mse',max_depth=3)
model.fit(X,y)#X 是40个点 y是一个圆
y_ = model.predict(X_test) #X_test是187点，预测y_应该是一个圆
# 请问y_中有多少数据？？？
print(y_.shape)
plt.figure(figsize=(6,6))
plt.scatter(y_[:,0],y_[:,1],color = 'green')
plt.savefig('./3-决策树回归效果.png',dpi = 200)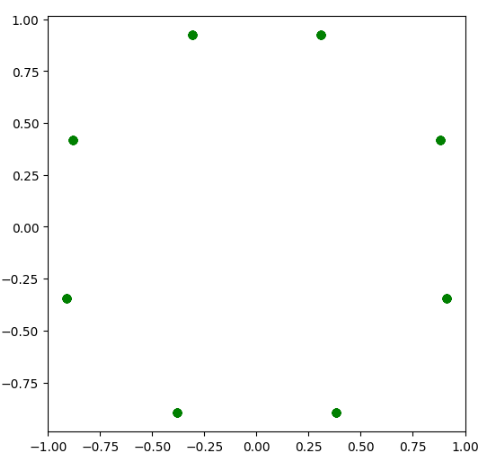

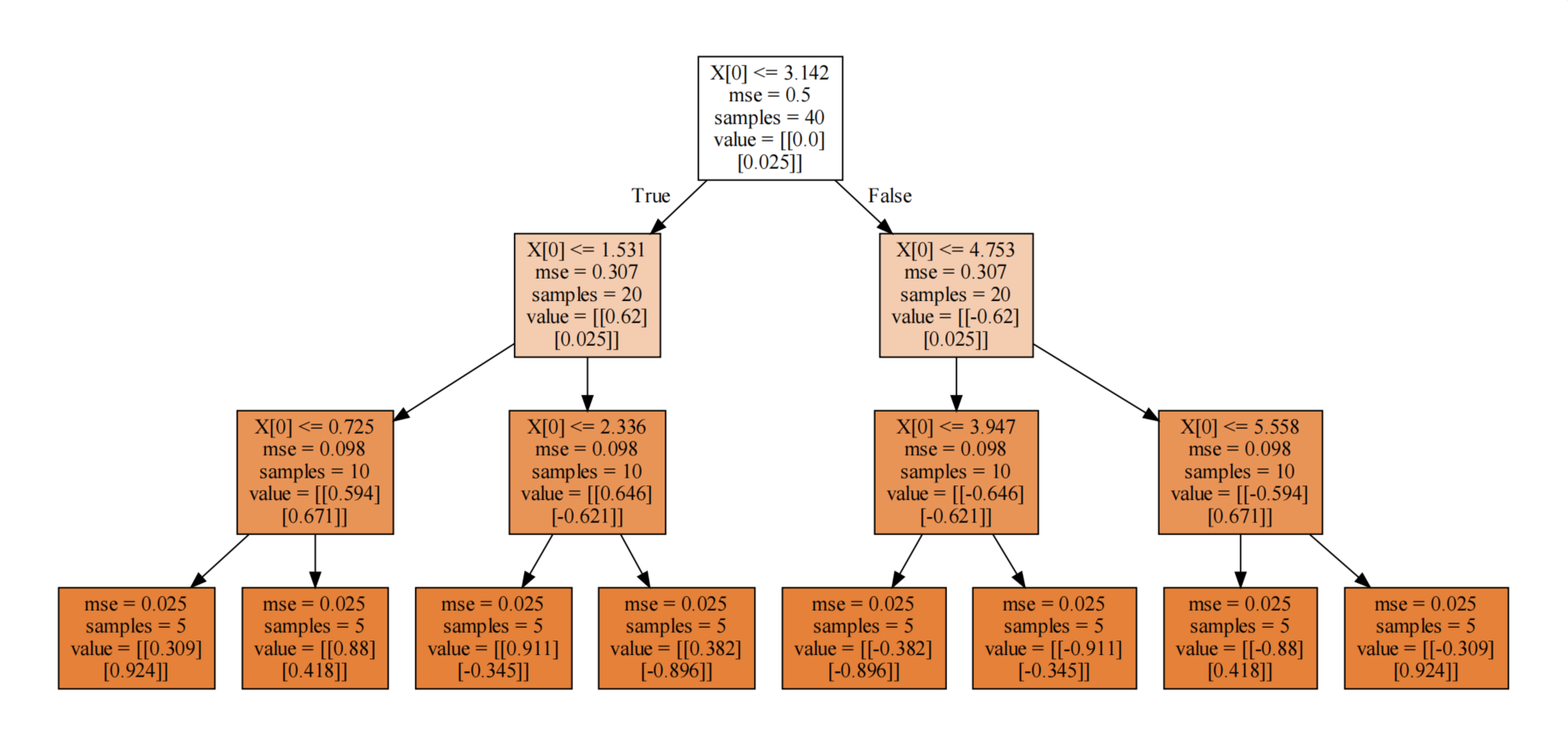
2.1.4 决策回归树可视化 

# 决策树形状
dot_data = tree.export_graphviz(model,filled=True)
graph = graphviz.Source(dot_data)
graph.render('./1-决策回归树')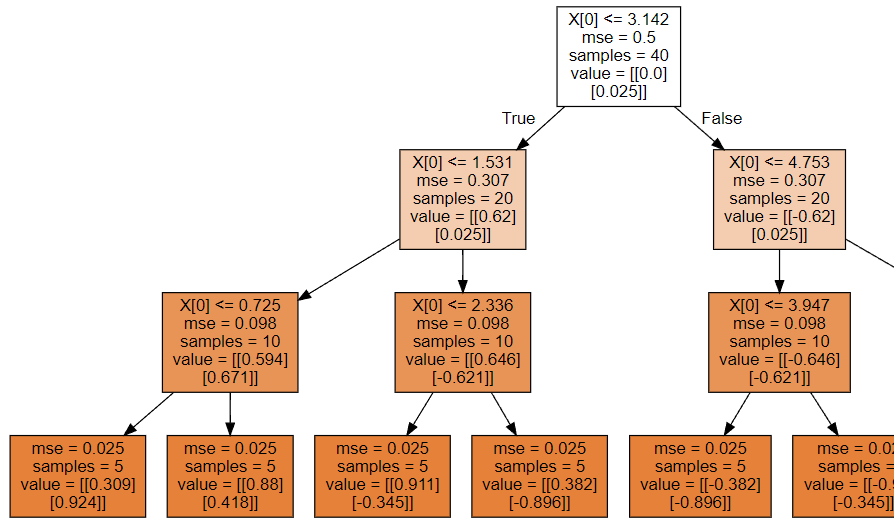

 因为决策树深度是3，所以最终得到8个叶节点，所以分成8类！

2.2、增加决策树深度

model = DecisionTreeRegressor(criterion='mse',max_depth=4)
model.fit(X,y)#X 是40个点 y是一个圆
y_ = model.predict(X_test) #X_test是187点，预测y_应该是一个圆
# 请问y_中有多少数据？？？
print(y_.shape)
plt.figure(figsize=(6,6))
plt.scatter(y_[:,0],y_[:,1],color = 'green')
plt.savefig('./4-增加深度决策树回归效果.png',dpi = 200)
# 决策树形状
dot_data = tree.export_graphviz(model,filled=True)
graph = graphviz.Source(dot_data)
graph.render('./5-增加深度决策回归树')

2.3、决策回归树分裂原理剖析

以上面深度为3的决策树为例

1、计算未分裂时，整体MSE:

\text{MSE}(y, \hat{y}) = \frac{1}{n_\text{samples}} \sum\limits_{i=0}^{n_\text{samples} - 1} (y_i - \hat{y}_i)^2

mse = ((y - y.mean(axis = 0))**2).mean()
print('未分裂时，整体MSE:',mse)

2、根据分裂标准X[0] <= 3.142，计算分裂后的MSE：

cond = X <= 3.142
part1 = y[cond.reshape(-1)]
part2 = y[(~cond).reshape(-1)]
mse1 = ((part1 - part1.mean(axis = 0))**2).mean()
mse2 = ((part2 - part2.mean(axis = 0))**2).mean()
print(mse1,mse2)

3、寻找最佳分裂条件：

split_result = {}
mse_lower = 0.5
for i in range(len(X) - 1):
    split = round(X[i:i + 2].mean(),3)
    cond = X <= split
    part1 = y[cond.reshape(-1)]
    part2 = y[(~cond).reshape(-1)]
    mse1 = ((part1 - part1.mean(axis = 0))**2).mean()
    mse2 = ((part2 - part2.mean(axis = 0))**2).mean()
    mse = mse1 * len(part1)/cond.size + mse2 * len(part2)/cond.size
    mse_result.append(mse)
    if mse < mse_lower:
        split_result.clear()
        split_result[split] = [i,mse]
        mse_lower = mse
print('最佳分裂条件：',split_result)

根据打印输出，我们知道最佳裂分，索引是：19。分裂条件是：3.142。

结论：和直接使用决策回归树绘图显示的结果一模一样~

3、决策回归树 VS 线性回归

1、加载数据  (糖尿病数据)

import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
diabetes = datasets.load_diabetes()#糖尿病
X = diabetes['data']
y = diabetes['target']
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 911)

2、线性回归表现

linear = LinearRegression()
linear.fit(X_train,y_train)
linear.score(X_test,y_test)    # 0.41394315401409987

3、决策树回归表现

import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'STKaiti'
max_depth = np.arange(1,16)
score = []
for d in max_depth:
    model = DecisionTreeRegressor(max_depth = d)
    model.fit(X_train,y_train)
    score.append(model.score(X_test,y_test))
plt.plot(max_depth,score,'ro-')
plt.xlabel('max_depth',fontsize = 18)
plt.ylabel('Score',fontsize = 18)
plt.title('决策树准确率随着深度变化',pad = 20,fontsize = 20)
plt.savefig('./6-决策树回归糖尿病.png',dpi = 200)

4、结论

  • 对于这个案例，线性回归效果更好一些

  • 糖尿病这个数据，更适合使用方程对规律进行拟合

  • 在很多方面，决策树回归表现也优秀~

4、集成算法

4.1、集成算法概述

集成算法核心：

  • 少数服从多数，人多力量大，三个臭皮匠顶个诸葛亮。

聚合模型：

  • 所有朋友的意见投票, 少数服从多数（随机森林对应原理公式）

G(x) = \frac{1}{n}\sum\limits_{i =1}^n1 \times g_i(x)

  • 牛一点的朋友多给几票，弱鸡一点的少给几票（Adaboost对应原理公式）

G(x) = \frac{1}{n}\sum\limits_{i =1}^n \alpha_i \times g_i(x) ;\alpha_i \ge 0

4.2、构造不同模型（朋友）

  • 同样的数据，行列都相同，不同的超参数，可以得到不同的模型。
  • 同样的超参数，行相同，列不同，可以得到不同的模型。
  • 同样的超参数，行不同，列相同，可以得到不同的模型。
  • 同样的超参数，同样的数据，但是数据权重不同，可以得到不同的模型。

4.3、集成算法不同方式

  • 方式一Bagging（套袋法）

    • 对训练集进行抽样， 将抽样的结果用于训练 g(x)。

    • 并行，独立训练。

    • 随机森林random forest便是这一类别的代表。

  • 方式二Boosting（提升法）

    • 利用训练集训练出模型，根据本次模型的预测结果，调整训练集。

    • 然后利用调整后的训练集训练下一个模型。

    • 串行，需要第一个模型。

    • Adaboost，GBDT，Xgboost都是提升树算法典型代表。

4.4、Bagging集成算法步骤

  1. Bootstrap（独立自主） : 有放回地对原始数据集进行均匀抽样

  2. 利用每次抽样生成的数据集训练模型

  3. 最终的模型为每次生成的模型进行投票

  4. 其实 boosting 和 bagging 都不仅局限于对决策树这种基模型适应

  5. 如果不是同一种 base model，也可以做集成算法

5、随机森林

5.1、随机森林介绍

Bagging 思想 + 决策树就诞生了随机森林。

随机森林，都有哪些随机？

  • bagging生成一颗决策树时，随机抽样

  • 抽样后，分裂时，每一个结点都随机选择特征，从部分特征中筛选最优分裂条件

5.2、随机森林实战

1、导包加载数据

import numpy as np
from sklearn import tree
from sklearn import datasets
from sklearn.model_selection import train_test_split
import graphviz
# ensemble 集成
# 随机森林
from sklearn.ensemble import RandomForestClassifier
# 作为对照
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
# 加载数据
X,y = datasets.load_iris(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 112)

2、普通决策树 

score = 0
for i in range(100):
    X_train,X_test,y_train,y_test = train_test_split(X,y)
    model = DecisionTreeClassifier()
    model.fit(X_train,y_train)
    score += model.score(X_test,y_test)/100
print('随机森林平均准确率是：',score)   #  0.9486842105263149

3、随机森林（运行时间稍长，10s） 

score = 0
for i in range(100):
    X_train,X_test,y_train,y_test = train_test_split(X,y)
    model = RandomForestClassifier()
    model.fit(X_train,y_train)
    score += model.score(X_test,y_test)/100
print('随机森林平均准确率是：',score)   # 随机森林平均准确率是： 0.9457894736842095

结论：

  • 和决策树对比发现，随机森林分数稍高，结果稳定

  • 即降低了结果方差，减少错误率

4、逻辑斯蒂回归 

import warnings
warnings.filterwarnings('ignore')
score = 0
for i in range(100):
    X_train,X_test,y_train,y_test = train_test_split(X,y)
    lr = LogisticRegression()
    lr.fit(X_train,y_train)
    score += lr.score(X_test,y_test)/100
print('逻辑斯蒂回归平均准确率是：',score)   #  0.9602631578947363

结论：

  • 逻辑斯蒂回归这个算法更加适合鸢尾花这个数据的分类

  • 随机森林也非常优秀

5.3、随机森林可视化

1、创建随机森林进行预测

X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 9)
forest = RandomForestClassifier(n_estimators=100,criterion='gini')
forest.fit(X_train,y_train)
score1 = round(forest.score(X_test,y_test),4)
print('随机森林准确率：',score1)         # 1.0
print(forest.predict_proba(X_test))

2、对比决策树 

X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 112)
model = DecisionTreeClassifier()
model.fit(X_train,y_train)
print('决策树准确率：',model.score(X_test,y_test))
proba_ = model.predict_proba(X_test)
print(proba_)

总结：

  • 一般情况下，随机森林比决策树更加优秀

  • 随机森林，是多棵树投票的概率，所以predict_proba()概率值，出现0.97

  • 单一决策树，不是，通过投票，而是通过决策树叶节点分类，所以概率要么是0，要么是1

3、绘制决策树 

dot_data = tree.export_graphviz(forest[0],filled=True)
graph = graphviz.Source(dot_data)
graph

# 第五十颗树类别
dot_data = tree.export_graphviz(forest[49],filled=True)
graph = graphviz.Source(dot_data)
graph

# 第100颗树类别
dot_data = tree.export_graphviz(forest[-1],filled=True)
graph = graphviz.Source(dot_data)
graph

5.4、随机森林总结

随机森林主要步骤：

  • 随机选择样本（放回抽样）；

  • 随机选择特征；

  • 构建决策树；

  • 随机森林投票（平均）

优点:

  • 表现良好

  • 可以处理高维度数据(维度随机选择)

  • 辅助进行特征选择

  • 得益于 Bagging 可以进行并行训练

缺点：

  • 对于噪声过大的数据容易过拟合

6、极限森林

6.1、极限森林介绍

极限森林，都有哪些随机？

  • 极限森林中每一个决策树都采用原始训练集

  • 抽样后，分裂时，每一个结点分裂时，都进行特征随机抽样（一部分特征作为分裂属性）

  • 从分裂随机中筛选最优分裂条件

6.2、极限森林实战

1、加载数据

import warnings
warnings.filterwarnings('ignore')
import numpy as np
from sklearn.ensemble import RandomForestClassifier,ExtraTreesClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
import graphviz
from sklearn import tree

# 加载数据
X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state = 119)

2、单棵决策树 

clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
print('单棵决策树得分：',clf.score(X_test,y_test))  # 0.9555555555555556
print('数据特征：',clf.n_features_)    # 13
print('节点分裂选择最大特征数量：',clf.max_features_)  # 13

3、随机森林 

clf2 = RandomForestClassifier()
clf2.fit(X_train,y_train)
print('随机森林得分：',clf2.score(X_test,y_test))  #  1.0
print('数据特征：',clf2.n_features_)   # 13
for t in clf2:
    print('节点分裂选择最大特征数量：',t.max_features_)    # 3

4、极限森林 

clf3 = ExtraTreesClassifier(max_depth = 3)
clf3.fit(X_train,y_train)
print('极限森林得分：',clf3.score(X_test,y_test))
print('数据特征：',clf3.n_features_)
for t in clf3:
    print('节点分裂选择最大特征数量：',t.max_features_)

5、可视化 

dot_data = tree.export_graphviz(clf3[0],filled=True)
graph = graphviz.Source(dot_data)

dot_data = tree.export_graphviz(clf3[49],filled=True)
graph = graphviz.Source(dot_data)

6、分裂标准代码演练

6.1、计算未分裂gini系数

count = []
for i in range(3):
    count.append((y_train == i).sum())
count = np.array(count)
p = count / count.sum()
gini = (p * (1 - p)).sum()
print('未分裂，gini系数是：',round(gini,3))  # 未分裂，gini系数是： 0.653

6.2、根据属性寻找最佳分裂条件

f = np.sort(X_train[:,11])
gini_lower = 1
best_split = {}
for i in range(len(f) - 1):
    split = round(f[i:i + 2].mean(),3)
    cond = X_train[:,11] <= split
    part1 = y_train[cond]
    part2 = y_train[~cond]
    # 计算每一部分的gini系数
    count1 = []
    count2 = []
    for j in range(3):
        count1.append((part1 == j).sum())
        count2.append((part2 == j).sum())
    count1,count2 = np.array(count1),np.array(count2)
    p1 = count1 / count1.sum()
    p2 = count2 / count2.sum()
    gini1 = round((p1 * (1 - p1)).sum(),3)
    gini2 = round((p2 * (1 - p2)).sum(),3)
    # 计算整体的gini系数
    gini = round(gini1 * count1.sum()/(y_train.size) + 
                 gini2 * count2.sum()/(y_train.size),3)
    if gini < gini_lower:
        gini_lower = gini
        best_split.clear()
        best_split[j] = split
    print(split,gini1,gini2,gini,count1,count2)
print(best_split,gini_lower)

结论：

  • 通过打印输出可知，极限森林分裂条件，并不是最优的

  • 并没有使用gini系数最小的分裂点

  • 分裂值，具有随机性，这正是极限森林的随机所在！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/345777.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Flink相关的记录

Flink相关的记录

Flink源码编译首次编译的时候&#xff0c;去除不必要的操作&#xff0c;同时install会把Flink中的module安装到本地仓库&#xff0c;这样依赖当前module的其他组件就无需去远程仓库拉取当前module&#xff0c;节省了时间。mvn clean install -T 4 -DskipTests -Dfast -Dmaven.c…
阅读更多...
对比Vector、ArrayList、LinkedList有何区别？

对比Vector、ArrayList、LinkedList有何区别？

第8讲 | 对比Vector、ArrayList、LinkedList有何区别&#xff1f; 我们在日常的工作中&#xff0c;能够高效地管理和操作数据是非常重要的。由于每个编程语言支持的数据结构不尽相同&#xff0c;比如我最早学习的 C 语言&#xff0c;需要自己实现很多基础数据结构&#xff0c;管…
阅读更多...
SpringCloud入门实战（六）-OpenFeign服务调用

SpringCloud入门实战（六）-OpenFeign服务调用

⭐️ SpringCloud 入门实战系列不迷路&#xff1a; SpringCloud 入门实战&#xff08;一&#xff09;什么是SpringCloud&#xff1f;SpringCloud 入门实战&#xff08;二&#xff09;-SpringCloud项目搭建SpringCloud 入门实战&#xff08;三&#xff09;-Eureka注册中心集成S…
阅读更多...
基于JAVA+SpringBoot+LayUI+Shiro的仓库管理系统

基于JAVA+SpringBoot+LayUI+Shiro的仓库管理系统

基于JAVASpringBootLayUIShiro的仓库管理系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ &#x1f345;文末获取项目下载方式&#x1f345; 一、项…
阅读更多...
React基础用法，脚手架创建项目。父子及兄弟通信，跨组件通信，定时器时钟案例

React基础用法，脚手架创建项目。父子及兄弟通信，跨组件通信，定时器时钟案例

create React App 脚手架工具创建项目1.下载插件2.打开终端npx create-react-app my-app //my-app是自己创建的项目名创建完成后cd my-app&#xff0c;到该项目的盘符执行npm start&#xff0c;就可以运行起来了组件通讯父传子在父亲组件中引用子组件在render&#xff08;&…
阅读更多...
基于商品理解的成交能力和成交满意度优化在Lazada的实践

基于商品理解的成交能力和成交满意度优化在Lazada的实践

作者&#xff1a;马蕊 Lazada推荐算法团队 在Lazada各域推荐场景中&#xff0c;既有优质商品优质卖家不断涌现带来的机会&#xff0c;也有商品质量参差带来的问题。如何才能为用户提供更好的体验&#xff0c;对卖家变化行为进行正向激励呢&#xff1f;下面本文将为大家分享我们…
阅读更多...
在TheSandbox 的「BOYS PLANET」元宇宙中与你的男孩们见面吧！

在TheSandbox 的「BOYS PLANET」元宇宙中与你的男孩们见面吧！

世界各的男孩们成为 K-Pop 男团的旅程。 Mnet 的全球项目 BOYS PLANET 终于在 2 月 2 日首次亮相&#xff01; The Sandbox 与 CJ ENM 合作&#xff0c;于 2 月 6 日晚上 10 点开始举办两个基于 BOYS PLANET 生存节目的虚拟体验&#xff1a;BOYS PLANET&#xff1a;BOYS LAND 和…
阅读更多...
五年制转本学历很重要江苏专转本

五年制转本学历很重要江苏专转本

五年制转本学历很重要&#xff01; 大专和本科是有区别的 越好的公司&#xff0c;越重要的职位&#xff0c;要求越高。 目前在中大型企业&#xff0c;除了销售、行政等岗位&#xff0c;其他普遍要求本科学历&#xff0c;有些可以放宽到大专。很多公司对于程序员等岗位的要求不仅…
阅读更多...
java中方法的学习笔记

java中方法的学习笔记

java中方法是完成特定的功能的&#xff0c;相对独立的程序段&#xff0c;与其他编程语言中的子程序&#xff0c;函数等概念相当。 方法一定义&#xff0c;就可以在不同的程序段中调用&#xff0c;因此方法可以增强程序的清晰度&#xff0c;提高编码的效率 方法的声明 [修饰符…
阅读更多...
装备制造业数字化转型CRM系统解决方案（信息图）

装备制造业数字化转型CRM系统解决方案（信息图）

一、制造企业面临的机遇与挑战 2021年12月28日&#xff0c;工业和信息化部等八部门联合对外发布《“十四五”智能制造发展规划》&#xff0c;明确提到“推进智能制造&#xff0c;要立足制造本质&#xff0c;紧扣智能特征&#xff0c;以工艺、装备为核心&#xff0c;以数据为基…
阅读更多...
jsp（全部知识点）

jsp（全部知识点）

&#x1f44c; 棒棒有言&#xff1a;也许我一直照着别人的方向飞&#xff0c;可是这次&#xff0c;我想要用我的方式飞翔一次&#xff01;人生&#xff0c;既要淡&#xff0c;又要有味。凡事不必太在意&#xff0c;一切随缘&#xff0c;缘深多聚聚&#xff0c;缘浅随它去。凡事…
阅读更多...
窗口置顶工具v2.6.0(截图+贴图)

窗口置顶工具v2.6.0(截图+贴图)

大家好&#xff0c;很高兴能再次更新版本&#xff0c;距上一年12月份到现在&#xff0c;有差不多两个月没有更新了&#xff0c;主要是年底&#xff0c;工作方面要冲刺&#xff0c;直到上周才有空继续开发置顶工具。 本来想再偷懒一段时间再开发&#xff0c;但最近在工作中经常…
阅读更多...
用于高效高光谱图像分类的多尺度上下文感知集成深度 KELM(Matlab代码实现）

用于高效高光谱图像分类的多尺度上下文感知集成深度 KELM(Matlab代码实现）

目录 &#x1f4a5;1 概述 &#x1f4da;2 运行结果 &#x1f389;3 参考文献 &#x1f468;‍&#x1f4bb;4 Matlab代码 &#x1f4a5;1 概述 高光谱遥感&#xff0c;作为成像技术与细分光谱技术有机结合的成像光谱遥感&#xff0c;可以获取在可见光到短波红外甚至中红外…
阅读更多...
重构之改善既有代码的设计(一)

重构之改善既有代码的设计(一)

1.1 何为重构&#xff0c;为何重构 第一个定义是名词形式&#xff1a; 重构&#xff08;名词&#xff09;&#xff1a;对软件内部结构的一种调整&#xff0c;目的是在不改变「软件可察行为」前提下&#xff0c;提高其可理解性&#xff0c;降低修改成本。 「重构」的另一个用…
阅读更多...
Bigscreen Beyond头显解析：极致轻量化，显示部分仅127g

Bigscreen Beyond头显解析：极致轻量化，显示部分仅127g

近年来&#xff0c;一体机占据了C端VR市场主要地位&#xff0c;其采用低成本、低门槛、无线化设计&#xff0c;对消费者足够友好。尽管如此&#xff0c;PC VR生态也在发展&#xff0c;相比于一体机&#xff0c;PC VR可提供视觉质量更高的VR体验&#xff0c;而且依托于SteamVR生…
阅读更多...
LayUI表格渲染实现前后端交互

LayUI表格渲染实现前后端交互

方法渲染 初始化 table 容器中配置好相应的参数&#xff0c;由 table 模块内部自动对其完成渲染&#xff0c;而无需你写初始的渲染方法。 首先满足&#xff1a; 带有 class"layui-table"的 标签&#xff1b;对标签设置属性lay-data"" 用于配置一些基础参…
阅读更多...
索引-性能分析-explain

索引-性能分析-explain

explain 执行计划 explain 执行计划各字段含义 1&#xff09;id 就是代表 sql 的执行顺序或者表的执行顺序&#xff1b;id相同从上往下执行&#xff0c;id不同&#xff0c;id值越大越先执行&#xff1b;&#xff08;注&#xff1a;有子查询时就会出现sql执行顺序&#xff09;…
阅读更多...
【物联网】mqtt初体验

【物联网】mqtt初体验

文章目录安装EMQXjava集成添加依赖mqtt配置参数发布组件订阅组件测试接口接口测试最近在了解物联网云平台方面的知识&#xff0c;解除了mqtt协议&#xff0c;只看书籍难免有些枯燥&#xff0c;所以直接试验一下&#xff0c;便于巩固理论知识。 broker服务器操作系统&#xff1a…
阅读更多...
Illegal char ＜:＞ at index 4

Illegal char ＜:＞ at index 4

一、现象Java11环境下项目启动时报错&#xff1a;java.nio.file.InvalidPathException: Illegal char <:> at index 4但项目能正常启动、运行。二、解决办法方法1方法2项目路径\.idea\workspace.xml中的PropertiesComponent节点下新增配置&#xff1a;<property name&…
阅读更多...
NoSQL(非关系型数据库)与SQL(关系型数据库)的差别

NoSQL(非关系型数据库)与SQL(关系型数据库)的差别

目录 NoSQL(非关系型数据库)与SQL(关系型数据库)的差别 1.数据结构&#xff1a;结构化与非结构化 2.数据关联&#xff1a;关联性与非关联性 3.查询方式&#xff1a;SQL查询与非SQL查询 4.事务特性&#xff1a;ACID与BASE 分析ACID与BASE的含义&#xff1a; 5.存储方式&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023