题目描述

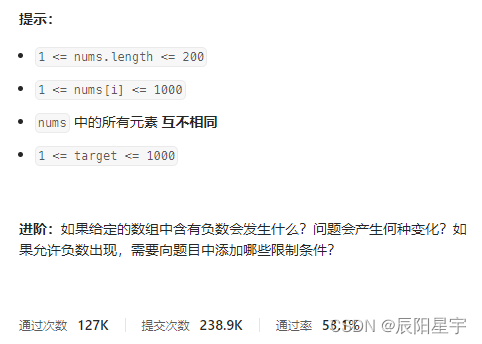
在这里插入图片描述

原题链接：377. 组合总和 Ⅳ

解题思路

一维滚动数组思路与 518. 零钱兑换 II（二维数组+一维滚动数组）大致相同，区别之处在于，零钱兑换解决的是组合问题（元素在不同位置都代表同一个含义），而该题解决的是排列问题（元素在不同位置代表不同的含义）。

对于解决完全背包累的一维滚动数组来说，
组合问题的遍历顺序是：先背包，再物品，从小到大遍历。
排列问题的遍历顺序时：先物品，再背包，从小到大遍历，内层要判定物品容量在规定范围内。

（1）二维数组

动态规划五步曲：

（1）dp[i][j]含义： 在目标和为j的前提下，从nums[0]-nums[i]中选数字，可以组成目标和j的方法个数。

（2）递推公式： 该递推公式与一般的完全背包递推公式不一样，牵扯到排列问题，不能直接使用化简后的式子dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]]，而应该在选取到每个i时，都把才能够0-i的组合再探查更新一遍，即递推公式为 sum(dp[i][j] + dp[i][j - nums[k]])（k属于0到i）

（3）dp数组初始化： dp[i][0] = 1，便于计算。

（4）遍历顺序： 由于是排列问题，遍历先背包，再物品，最内层没遍历到一个物品i，都从0-i再遍历更新一遍。

（5）举例： （省略）

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        int dp[201][1001] = {0};
        int n = nums.size();
        for(int i = 0; i <= n; i++)         dp[i][0] = 1;

        for(int j = 1; j <= target; j++) {
            for(int i = 1; i <= n; i++) {
                for(int k = i; k > 0; k--) {
                    if(j - nums[k - 1] >= 0 && dp[i][j] < INT_MAX - dp[i][j - nums[k - 1]]) {
                        dp[i][j] += dp[i][j - nums[k - 1]];
                    }   
                }
            }
        }

        return dp[n][target];
    }
};

（2）一维滚动数组

递推公式变为与二维等价式 dp[j] += dp[j - nums[i - 1]]，遍历顺序先背包，再物品，因为每次是基于上一次结果的滚动技术，因此不用再才从0-i遍历一遍。思路与 518. 零钱兑换 II（二维数组+一维滚动数组）大致相同。

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        int dp[1001] = {0};
        int n = nums.size();
        dp[0] = 1;

        for(int j = 1; j <= target; j++) {
            for(int i = 1; i <= n; i++) {
                // 因为测试用例有有dp[j] + dp[j - nums[i - 1]]超过MAX_INT，因此要判定并且用减法式子判定
                if(nums[i - 1] <= j && dp[j] < INT_MAX - dp[j - nums[i - 1]]) {
                    dp[j] += dp[j - nums[i - 1]];
                }
            }
        }

        return dp[target];
    }
};