作者：指针不指南吗
专栏：算法篇

🐾要学会在纸上打草稿，这个很重要🐾

前缀和 主打一个记公式

1.什么是前缀和？

原数组

a1 , a2 , a3 , a4 , a5 , a6 , a7

前缀和

s1=a1;

s2=a1+a2;

s3=a1+a2+a3;

…

si=a1+a2+a3+…+ai

前缀和实际就是数组前 i 项和

---

2.怎么求前缀和？

结合定义，解释的很清楚，前 i 项相加即可

思路：第 i 个前缀和就 = 前一个前缀和 + 第 i 个元素

但是注意！！！循环开始从1开始,s0=0;

• 第一种

  易懂但用两个数组

for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
    	s[i]+=a[i];
	}

• 第二种

  优化版：只需要一个数组

for(int i=1;i<=;i++){
		scanf("%d",&s[i]);
		s[i]+=s[i-1];
	}

---

3.前缀和有什么用？

作用只有一个：求区间和

求区间使用前缀和可以降低时间复杂度，更加方便

求区间[l,r]中元素的和：

s [ l ~ r ] = s [ r ] - s [ l -1 ]

这里解释了为什么写前缀和的时候，从1开始，并且s0=0 通用的，对 s[1~

n]也适用

例如,求数组第a个到第b个的子数组的和

 while(m--){
        int a,b;
        cin>>a>>b;
        cout<<s[b]-s[a-1]<<endl;
    }

4.进阶二维:矩阵和

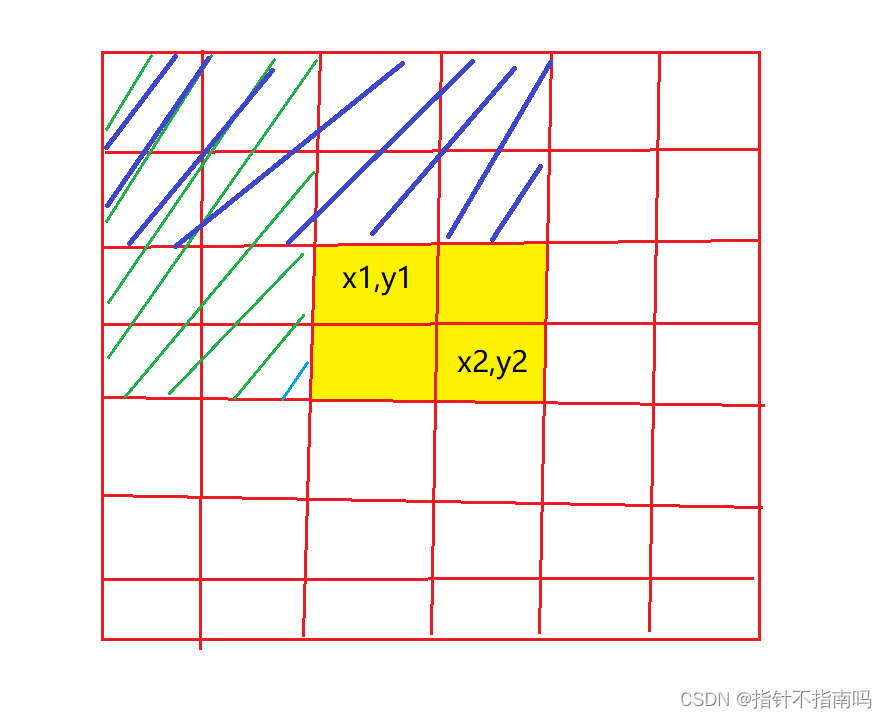
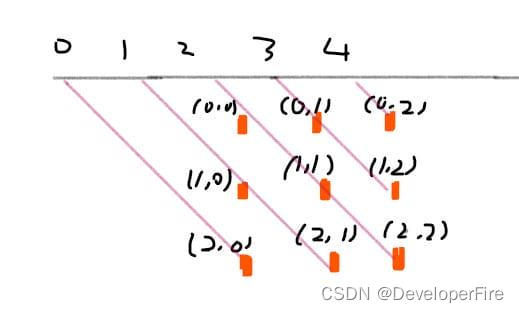
求黄色部分的子矩阵和

黄=整个-绿-蓝+混

S[i, j] = 第i行j列格子左上部分所有元素的和

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：

S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

• 代码实现

#include<iostream>
using namespace std;

const int N=1010;

int s[N][N];

int n,m,q;

int main(){
    cin>>n>>m>>q;
    
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            cin>>s[i][j];
            s[i][j]+=s[i-1][j]+s[i][j-1]+s[i-1][j-1];
        }
    
    while(q--){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
    }
    return 0;
}