为什么要进行模型评估？- 选择模型与参数

在现实任务中，我们往往有多种学习算法可供选择，甚至对同一个学习算 法，当使用不同的参数配置时，也会产生不同的模型.那么，我们该选用哪一个学习算法、使用哪一种参数配置呢？这就是机器学习中的“模型选择”(model selection)问题。

理想的解决方案当然是对候选模型的泛化误差进行评估，然后选择泛化误差最小的那个模型。然而，实际问题总无法直接获得泛化误差（因为事先并不知道新样本是什么样），实际能做的是努力使训练误差（又称经验误差）最小化，而训练误差又由于过拟合现象的存在而不适合作为标准。

可通过实验测试来对学习器的泛化误差进行评估并进而做出选择。

在何种数据集上对训练误差进行评估？- 训练集

在何种数据集上对泛化误差进行评估？- 测试集

“测试集”(testing set)来测试学习器对新样本的判别能力，然后以测试集上的“测试误差”(testing error)作为泛化误差的近似。

如何划分测试集？

测试样本也是从样本真实分布中独立同分布采样而得。但需注意的是，测试集应该尽可能与训练集互斥，即测试样本尽量不在训练集中出现、未在训练过程中使用过（可理解为学生偷看过答案去闭卷考试，该考试没预测出该学生的能力）。

1 留出法

“留出法”(hold-out)直接将数据集划分为两个互斥的集合，其中一个集合作为训练集S，另一个作为测试集T，即 0 = S U T, S n T = 0。在 S 上训练出模型后，用 T 来评估其测试误差，作为对泛化误差的估计。

需注意的是，训练/测试集的划分要尽可能保持数据分布的一致性，避免因数据划分过程引入额外的偏差而对最终结果产生影响，例如在分类任务中至少要保持样本的类别比例相似。

如果从采样(sampling)的角度来看待数据集的划分过程，则保留类别比例的采样方式通常称为“分层采样 "(stratified sampling)。若划分后的训练集、测试集中样本类别比例差别很大，则误差估计将由于训练/测试数据分布的差异而产生偏差。

2 交叉验证法

3 自助法

模型选择和调参的区别？

大多数学习算法都有些参数(parameter)需要设定，参数配置不同，学得模型的性能往往有显著差别。因此，在进行模型评估与选择时，除了要对适用学习算法进行选择，还需对算法参数进行设定，这就是通常所说的“参数调节”或简称“调参” (parameter tuning)。

在研究对比不同算法的泛化性能时，用测试集上的判别效果来估计模型在实际使用时的泛化能力，而把训练数据另外划分为训练集和验证集，基于验证集上的性能来进行模型选择和调参。

如何模型选择？

模型选择：对每种参数配置都训练出模型，然后把对应最好模型的参数作为结果。

如何调参？

调参：学习算法的很多参数是在实数范围内取值，因此，对每种参数配置都训练出模型来是不可行的。现实中常用的做法，是对每个参数选定一个范围和变化步长，例如在$[0,0.2]$范围内以0.05为步长，则实际要评估的候选参数值有5个，最终是从这5个候选值中产生选定值。显然，这样选定的参数值往往不是“最佳”值，但这是在计算开销和性能估计之间进行折中的结果，通过这个折中，学习过程才变得可行。事实上，即便在进行这样的折中后，调参往往仍很困难。

可以简单估算一下：假定算法有3个参数，每个参数仅考虑5个候选值，这样对每一组训练/测试集就有53 = 125个模型需考察；很多强大的学习算法有大量参数需设定，这将导致极大的调参工程量，以至于在不少应用任务中, 参数调得好不好往往对最终模型性能有关键性影响。

什么是最终模型？

给定包含m个样本的数据集D，在模型评估与选择过程中由于需要留出一部分数据进行评估测试，事实上只使用了一部分数据训练模型。因此，在模型选择完成后，学习算法和参数配置已选定，此时应该用数据集D重新训练模型。这个模型在训练过程中使用了所有m个样本，这才是最终提交给用户的模型。

如何评估模型（性能度量）？

性能度量反映了任务需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果；这意味着模型的“好坏”是相对的，什么样的模型是好的，不仅取决于算法和数据，还决定于任务需求。

要评估学习器的性能，就要把学习器预测结果与真实标记进行比较。

如何对模型泛化性能评估？

对学习器的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是性能度量(performance measure)。

如何评估回归任务模型？- 评价标准：均方误差

回归任务最常用的性能度量是“均方误差"(mean squared error)。

如何评估分类任务模型？- 评价标准：错误率、精度、查全率、查准率、P-R、ROC

错误率 & 精度

错误率和精度是分类任务中最常用的两种性能度量，既适用于二分类任务，也适用于多分类任务。

错误率：分类错误的样本数占样本总数的比例。

精度：分类正确的样本数占样本总数的比例。

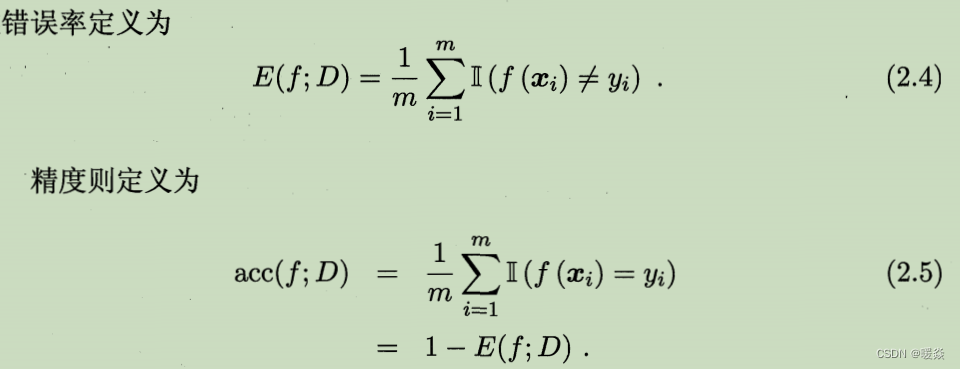
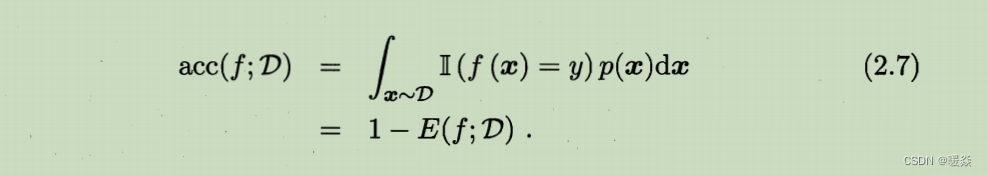
有哪些错误率和精度不适用的任务需求？

错误率和精度虽常用，但并不能满足所有任务需求。以西瓜问题为例，假定瓜农拉来一车西瓜，用训练好的模型对这些西瓜进行判别，显然，错误率衡量了有多少比例的瓜被判别错误。但是若我们关心的是“挑出的西瓜中有多少比例是好瓜”，或 者 “所有好瓜中有多少比例被挑了出来”，那么错误率显然就不够用了，这时需要使用其他的性能度量。

类似的需求在信息检索、Web搜索等应用中经常出现，例如在信息检索中，经常会关心 “检索出的信息中有多少比例是用户感兴趣的” “用户感兴趣的信息中有多少被检索出来了”。 “查准率”(precision)与 “查全率”(recall)是更为适用于此类需求的性能度量。

查准率（准确率）、查全率（召回率）、$F_{\beta }$、$F_1$

如何评估二分类问题模型？- P-R

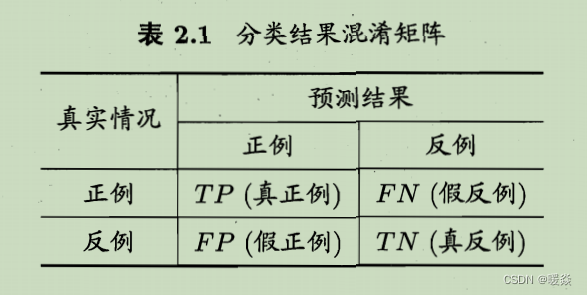
二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为 真正例(true positive)、假正例(false positive)、真反例(true negative)、假反例(false negative)四种情形，令 TP、FP、T N、FN 分别表示其对应的样例数，则显然有TP + FP + TN + FN = 样例总数。分类结果的混淆矩阵 (confusion matrix) 如下图所示。

为什么P-R曲线可以评估模型性能？- P&R度量不同情况的准确率

以西瓜问题为例，假定瓜农拉来一车西瓜，用训练好的模型对这些西瓜进行判别，显然，错误率衡量了有多少比例的瓜被判别错误。但是若我们关心的是“挑出的西瓜中有多少比例是好瓜”，或 者 “所有好瓜中有多少比例被挑了出来”，那么错误率显然就不够用了，这时需要使用其他的性能度量。

类似的需求在信息检索、Web搜索等应用中经常出现，例如在信息检索中，经常会关心 “检索出的信息中有多少比例是用户感兴趣的” “用户感兴趣的信息中有多少被检索出来了”。 “查准率”(precision)与 “查全率”(recall)是更为适用于此类需求的性能度量。

查准率和查全率是一对矛盾的度量。一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。

例如，若希望将好瓜尽可能多地选出来，则可通过增加选瓜的数量来实现，如果将所有西瓜都选上，那么所有的好瓜也必然都被选上了，但这样查准率就会较低；若希望选出的瓜中好瓜比例尽可能高，则可只挑选最有把握的瓜，但这样就难免会漏掉不少好瓜，使得查全率较低。通常只有在一些简单任务中，才可能使查全率和查准率都很高。

如何画P-R曲线？- 排序&求PR

1 根据学习器的预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本。

2 按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率。

3 以查准率为纵轴、查全率为横轴作图，就得到了查准率-查全率曲线，简称 “P-R曲线”。显示该曲线的图称为“P-R图”。

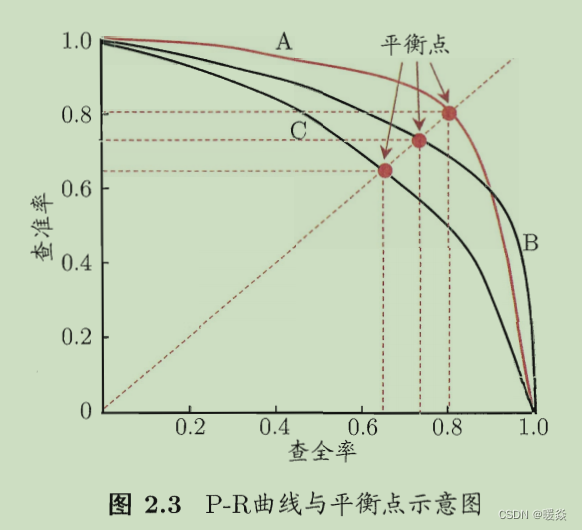
为绘图方便和美观，示意图显示出单调平滑曲线；但现实任务中的P-R曲线常是非单调、不平滑的，在很多局部有上下波动。

如何利用P-R曲线进行性能度量？- 包围 & 面积 & BEP & Fβ

曲线无交叉：若一个学习器的 P-R 曲线被另一个学习器的曲线完全“包住”，则可断言后者的性能优于前者。

曲线有交叉：P-R曲线下面积大小 -> 平衡点BEP -> $F_{\beta }$ -> $F_1$

曲线有交叉时，难以一般性地断言两者孰优孰劣，只能在具体的查准率或查全率条件下进行比较。然而，在很多情形下，人们往往仍希望把学习器A 与 B 比出个高低。这时一个比较合理的判据是比较P-R曲线下面积的大小。

P-R曲线下面积：在一定程度上表征了学习器在查准率和查全率上取得相对“双高”的比例。但这个值不太容易估算，因此，人们设计了一些综合考虑查准率、查全率的性能度量。

平衡点（Break-Event Point，BEP）：“查准率 = 查全率”时的取值，BEP越大，学习器越优。BEP还是过于简化了些，更常用的是$F_1$度量。

$F_{\beta }$度量：在一些应用中 ，对查准率和查全率的重视程度有所不同。例如在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容确是用户感兴趣的，此时查准率更重要；而在逃犯信息检索系统中，更希望尽可能少漏掉逃犯，此时查全率更重要，$\beta$的取值能表达出对查准率/查全率的不同偏好。$\beta <1$ 查准率有更大影响，$\beta >1$ 查准率有更大影响，$\beta >1$ 查准率与查全率同样的影响。

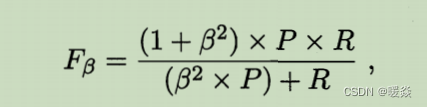
N 二分类问题 模型评估

很多时候有多个二分类混淆矩阵，例如进行多次训练/测试，每次得到一个混淆矩阵；或是在多个数据集上进行训练/测试，希望估计算法的“全局”性能；甚或是执行多分类任务，每两两类别的组合都对应一个混淆矩阵；总之，希望在n个二分类混淆矩阵上综合考察查准率和查全率。

如何计算 N 二分类问题的PR值？- 宏 & 微

方法一：各自计算PR后求全部PR平均（宏）

方法二：求TP、FP、TN、FN平均后求PR平均（微）

ROC & AUC

为什么ROC曲线可以评估模型性能？- ROC评估排序质量

根据学习器的预测结果对样例进行排序。

ROC、AUC 考虑的是样本预测的排序质量。

ROC、AUC 是从排序质量角度出发来研究学习器泛化性能的有力工具。

排序本身的质量好坏，体现了综合考虑学习器在不同任务下的“期望泛化性能”的好坏，或者说，“一般情况下”泛化性能的好坏。

如何画ROC曲线？

1 根据学习器的预测结果对样例进行排序。

2 按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量，分别是 “假正例率”(False Positive Rate，FPR)、“真正例率”(True Positive Rate，TPR) 。

3 以假正例率为横轴、真正例率为纵轴作图，最后得到 “ROC 曲线”。显示ROC曲线的图称为“ROC图”。

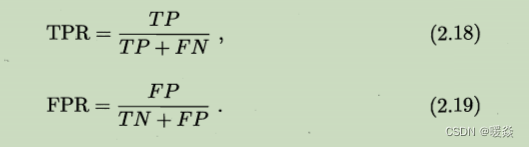
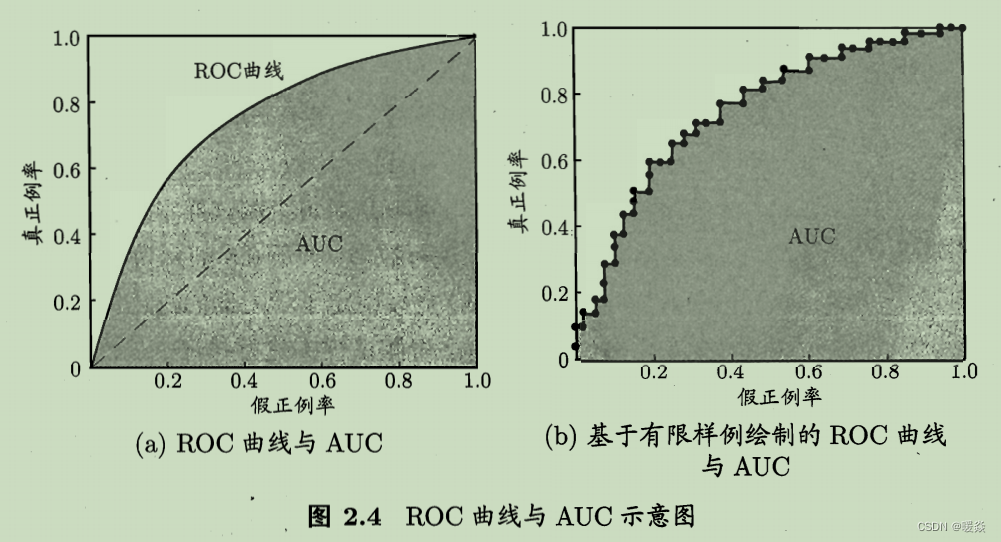
对角线对应于“随机猜测”模型，而点(0, 1)则对应于将所有正例排在所有反例之前的“理想模型”。

现实任务中通常是利用有限个测试样例来绘制ROC图，此时仅能获得有限个(真正例率，假正例率)坐标对，无法产生图2.4(a)中的光滑ROC曲线，只能绘制出如图2.4(b)所示的近似ROC曲线。

如何利用ROC曲线性能度量？ - 比较曲线

进行学习器的比较时，与 P-R 图相似。

曲线无交叉：若一个学习器的ROC曲线被另一个学习器的曲线完全“包住"则可断言后者的性能优于前者；

曲线有交叉：若两个学习器的 ROC 曲线发生交叉，则难以一般性地断言两者孰优孰劣。此时如果一定要进行比较，则较为合理的判据是比较ROC曲线下的面积，即 AUC (Area Under ROC Curve）。面积越大，模型更优。

如何求近似ROC曲线？

AUC 可通过对 ROC 曲线下各部分的面积求和而得。

AP

mAP