线段树
- 由来
- 算法讲解分析
- 树的数据结构
- 结点
- 四个基本操作
- 例题
- 天才的记忆
- 最大数
由来
线段树是RMQ区间最值问题的一种解题方法,在给出的区间是静态不变的时候,可以使用ST算法进行离线查询某个区间的最值,先预处理后进行m次查询,时间复杂度为O(nlogn+m* 1)=O(nlogn),详情参考我的这篇博客:RMQ问题
但是当区间是不断变化的,在区间变化的同时进行询问的情况ST算法时间复杂度会达到O(m*nlogn)每次区间变化后都要重新进行预处理,不适用,此时就需要用到线段树
算法讲解分析
树的数据结构
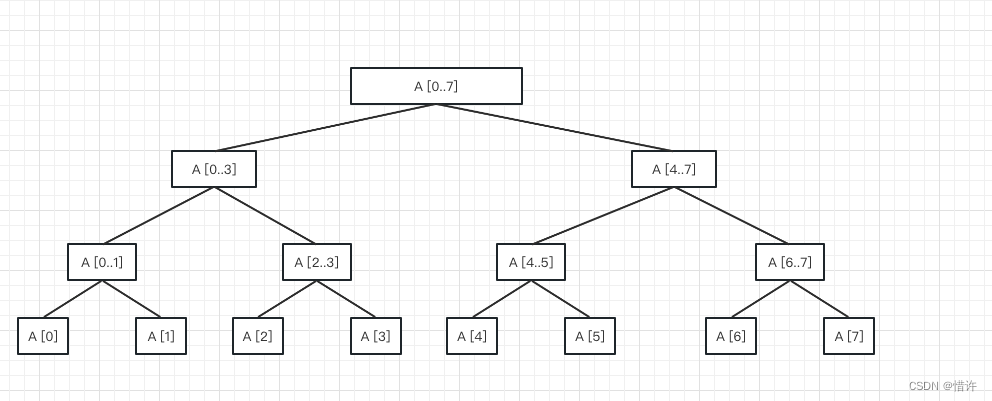
线段树是一个完美的完全满二叉树(除了最后一层其他层都是慢得,并且除了叶子结点外每个结点都既有左孩子也有右孩子)
那么对于这个树的存储就可以用堆的方式来存储,即用一维数组存树
对于树中的每个结点编号为x,其父节点编号为x/2(x>>1),左儿子为2x(x<<1),右儿子为2*x+1(x<<1|1),当然需要满足根节点编号从1开始,如果从0开始就会比较麻烦。
结点
树的每个结点对应一个区间,根节点表示所有元素所在区间,结点的左孩子表示该区间的左半部分,右孩子表示该区间的右半部分,结点存储所表示区间的左端点和右端点,以及该区间的最值。定义结构体如下:
typedef struct Node
{
int l;int r;int Max;
}T;
用一个图来表示结点间的关系,假设给定的元素区间为[1,10]一共十个元素
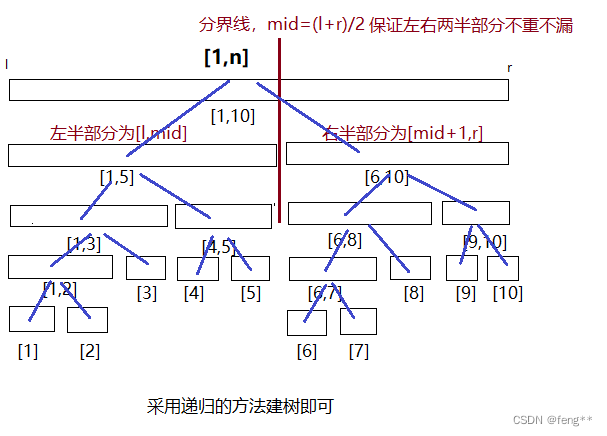
考虑一共大致会有多少个结点,以便于决定开多大的数组空间来存树,倒数第二层最坏的情况下大概是n个,每个区间大小都为1,因此,除去最后一层,其他层的所有结点个数为2n-1(n+n/2+n/4+…+1等比数列前n项和),最后一层最多为2n个,因此整棵树的结点个数最多为2n-1+2n,大致为4n个,因此数组开4n就够了。
四个基本操作
pushup(id): 用子节点信息更新父节点的信息
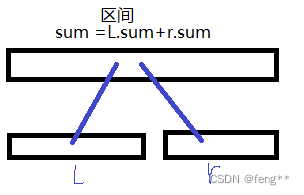
代码:用左右孩子的结点值更新父节点的值
void pushup(int id)
{
tree[id].Max=max(tree[id*2].Max,tree[id*2+1].Max); //父节点的最大值取左右孩子的最大值
}
build(id,l,r): 建树,将一段区间初始化为一棵线段树,如果一开始的区间为空,在后续才逐渐向区间内添加元素的话就先建立一棵空的树,只需要表达结点之间的关联即可
代码:
void build(int id,int l,int r) //建立左端点为l,右端点为r的区间对应的结点,结点编号为id
{
tree[id].l=l;
tree[id].r=r;
if(l==r)
{
//tree[id].Max=num; 如果是空树就不需要给叶子结点赋值
return ; //区间长度为1,只剩一个元素了
}
int mid=l+r>>1;
build(2*id,l,mid); //建立左子树
build(2*id+1,mid+1,r); //建立右子树
//pushup(id); 如果最开始建立的是一个空壳树就不需要向上传递信息
}
query(id,l,r): 查询[l,r]区间信息,比如求这个区间的最值
查询和修改都涉及到定位到某个元素或者某段区间的问题,二者的解决思路是一样的,并且定位到某个元素实际也可以看成是一段只有一个元素的区间,因此,只需要实现在总区间内定位某个区间的最值就行
假设[l,r]为待查区间,[tr,tl]为当前树结点对应的区间,从根节点不断递归往下搜索待查区间内的最值,待查区间和当前树结点对应的区间有以下两种对应关系:

线段树在区间比较短时的查询是比较慢的,但是总体查询和修改过程中访问过的区间(结点)数量一定在logn范围内,大致为4logn(树状数组只有logn)
modify(id): 修改树,修改某个结点或者修改某个区间的值
修改单点值:modify(id,x,v) 修改x位置元素为v,直接递归往下找到对应的点,回溯的时候更新一下父节点的值即可,easy
代码:
void modify(int id,int n,LL v) //修改单点数,将第n位的值改为v
{
int tl=tree[id].l,tr=tree[id].r;
if(tl==tr) //定位到要修改的点了,区间大小为1,此时tl=tr=n
{
tree[id].Max=v; return ;
}
int mid=tl+tr>>1;
if(n<=mid) modify(2*id,n,v); //跟结点左孩子(区间左边)有交集,修改点属于左区间
else if(mid<n) modify(2*id+1,n,v); //跟结点右孩子(区间右边)有交集 ,修改点属于右区间
pushup(id); //修改子树后向上更新一下最最值
}
修改区间值:pushdown操作延迟更新,将父节点的信息下传到子节点(懒标记、延迟标记),区间内所有元素加上一个数,递归将左右区间分别加上这个数
例题
天才的记忆
题目链接: https://www.acwing.com/problem/content/description/1275/
思路分析: 这个题是标准的RMQ问题,并且是数组固定的(离线做法)情况,因此用ST算法会更快一些,时间复杂度能控制在O(nlogn预处理+m查询),用线段树有点大材小用了,时间复杂度为O(nlogn建树+mlogn单次操作),只需要按照模板将树建立起来,然后做查询即可
AC代码:
#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;
const int N=200005;
typedef struct Node
{
int l;int r;int Max;
}T;
T tree[4*N];
int num[N];
int n,m,x,y;
void pushup(int id)
{
tree[id].Max=max(tree[id*2].Max,tree[id*2+1].Max);
}
void build(int id,int l,int r)
{
tree[id].l=l;
tree[id].r=r;
if(l==r)
{
tree[id].Max=num[l];return ;
}
int mid=l+r>>1;
build(2*id,l,mid);
build(2*id+1,mid+1,r);
pushup(id);
}
int query(int id,int l,int r)
{
int tl=tree[id].l,tr=tree[id].r;
if(tl>=l&&tr<=r) return tree[id].Max;
int mid=tl+tr>>1;
int ans=-0x3f3f3f3f;
if(l<=mid) ans=query(2*id,l,r);
if(r>mid) ans=max(ans,query(2*id+1,l,r));
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&num[i]);
}
scanf("%d",&m);
build(1,1,n);
while(m--)
{
scanf("%d %d",&x,&y);
printf("%d\n",query(1,x,y));
}
return 0;
}
最大数
题目链接: https://www.acwing.com/problem/content/description/1277/
思路分析: 这个题也是区间最值问题,但是如果用ST算法,每次往区间内插入数都需要对dp数组进行初始化,导致时间复杂度为O(mnlogn)了,肯定会超时,因此只能采用线段树的在线做法。
不能把往数组尾部插入数看做是区间在不断地变化,这样的话每次插入一个数都需要重新build树,就没有实现线段树做法,导致超时,因为build的时间复杂度为O(nlogn)。实际一开始将数组看做是有数的,只不过取值为0或者负无穷,每次往数组末尾插入一个数,看做是修改区间内第n个数的值,线段树的修改和查询时间复杂度能保证在O(4logn)内,因此总的时间复杂度保证为O(mlogn)。
一开始就用所有元素初始化树,但是在这道题中一开始的区间元素没给出来,表面看是空的,实际上我们当做是0,区间大小考虑最坏m次都是插入操作,则区间为[1,m]。
AC代码:
#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long LL;
const int N=200005;
typedef struct Node
{
int l;int r;LL Max;
}T;
T tree[4*N];
LL p; //值要开long long
int m; //区间的总长度最大为m(所有m次操作都是插入数操作)
void pushup(int id)
{
tree[id].Max=max(tree[id*2].Max,tree[id*2+1].Max); //父节点的最大值取左右孩子的最大值
}
void build(int id,int l,int r)
{
tree[id].l=l;
tree[id].r=r;
if(l==r) return ;
int mid=l+r>>1;
build(2*id,l,mid); //建立左子树
build(2*id+1,mid+1,r); //建立右子树
//pushup(id); 如果最开始建立的是一个空壳树就不需要向上传递信息
}
LL query(int id,int l,int r) //查询[l,r]区间内的最值
{
int tl=tree[id].l,tr=tree[id].r;
if(tl>=l&&tr<=r) //[tl,tr]区间属于[l,r]区间,直接返回
{
return tree[id].Max;
}
int mid=tl+tr>>1;
// if(l<=mid) return query(2*id,l,r); //跟结点左孩子(区间左边)有交集
// else if(mid<=r) return query(2*id+1,l,r); //跟结点右孩子(区间右边)有交集
// 上面这种写法是错的,如果同时跟左边和右边都有交集,只会在查询了左边后就返回了
LL ans=0;
if(l<=mid) ans=query(2*id,l,r); //跟结点左孩子(区间左边)有交集
if(mid<r) ans=max(ans,query(2*id+1,l,r)); //跟结点右孩子(区间右边)有交集
return ans;
}
void modify(int id,int n,LL v) //修改单点数,将第n位的值改为v
{
int tl=tree[id].l,tr=tree[id].r;
if(tl==tr) //定位到要修改的点了,区间大小为1,此时tl=tr=n
{
tree[id].Max=v; return ;
}
int mid=tl+tr>>1;
if(n<=mid) modify(2*id,n,v); //跟结点左孩子(区间左边)有交集,修改点属于左区间
else if(mid<n) modify(2*id+1,n,v); //跟结点右孩子(区间右边)有交集 ,修改点属于右区间
pushup(id); //修改子树后向上更新一下最最值
}
int main()
{
scanf("%d %ld",&m,&p);
build(1,1,m);
int n=0,t=0;
LL a=0;
while(m--)
{
getchar();
char c;scanf("%c %d",&c,&t);
if(c=='Q') //查询操作
{
a=query(1,n-t+1,n);
printf("%d\n",a); //待查询区间
}
else
{
n++; //更新插入数的位置
modify(1,n,(t+a)%p); //修改线段树
}
}
return 0;
}