前言

线段树是一种二叉搜索树，线段树的每个结点都存储了一个区间，也可以理解成一个线段，在这些线段上进行搜索操作得到你想要的答案。

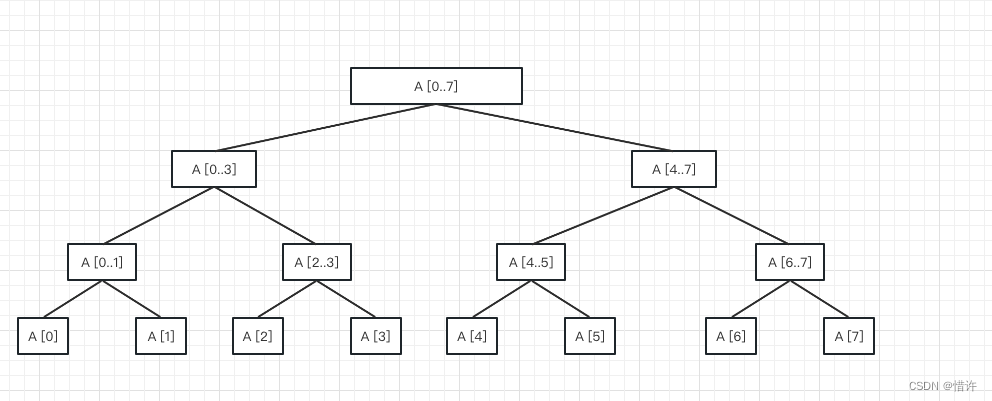
线段树的适用范围很广，可以在线维护修改以及查询区间上的最值，求和。更可以扩充到二维线段树（矩阵树）和三维线段树（空间树）。对于一维线段树来说，每次更新以及查询的时间复杂度为O(logN)。

代码实现

package com.sjgd.segmenttree;

import androidx.annotation.NonNull;

/**
 * @author 自定义线段树
 * on 2023/2/13
 */
public class SegmentTree<E> {
    private E[] data;

    private E[] tree;

    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger merger) {
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }
        tree = (E[]) new Object[4 * arr.length];
        this.merger = merger;
        buildSegmentTree(0, 0, data.length - 1);

    }

    /**
     * 在treeIndex的位置创建表示区间[l,r]的线段树
     *
     * @param treeIndex
     * @param l
     * @param r
     */
    private void buildSegmentTree(int treeIndex, int l, int r) {
        if (l == r) {
            tree[treeIndex] = data[l];
            return;
        }
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        int mid = l + (r - l) / 2;
        //需要分别在[l,mid]以及[mid+1,r]区间上创建线段树
        buildSegmentTree(leftTreeIndex, l, mid);
        buildSegmentTree(rightTreeIndex, mid + 1, r);
        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

    public int getSize() {
        return data.length;
    }

    public E get(int index) {
        if (index < 0 || index > data.length - 1) {
            throw new IllegalArgumentException("Index is Illegal.");
        }
        return data[index];
    }

    /**
     * 返回二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
     */
    private int leftChild(int index) {
        return 2 * index + 1;
    }

    /**
     * 返回二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
     */
    private int rightChild(int index) {
        return 2 * index + 2;
    }

    /**
     * 查询线段树中[queryL,queryR]区间的数据并返回
     *
     * @return
     */
    public E query(int queryL, int queryR) {
        if (queryL < 0 || queryL > tree.length - 1 || queryR < 0 || queryR > tree.length - 1 || queryL > queryR) {
            throw new IllegalArgumentException("Index is Illegal");
        }
        return query(0, 0, data.length - 1, queryL, queryR);
    }

    private E query(int treeIndex, int l, int r, int queryL, int queryR) {
        if (l == queryL && r == queryR) {
            return tree[treeIndex];
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if (queryR <= mid) {
            //说明[queryL,queryR]区间全部落在[l,mid]区间上，直接去左子树中查找即可
            return query(leftTreeIndex, l, mid, queryL, queryR);
        } else if (queryL >= mid + 1) {
            //说明[queryL,queryR]区间全部落在[mid+1,r]区间上，直接去右子树中查找即可
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
        }

        //需要分别在[queryL,mid]区间以及[mid+1,r]
        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);

        return merger.merge(leftResult, rightResult);
    }

    /**
     * 修改index位置数组元素的值为e
     * @param index
     * @param e
     */
    public void set(int index, E e) {
        if (index < 0 || index > data.length - 1) {
            throw new IllegalArgumentException("Index is Illegal.");
        }
        data[index] = e;
        set(0, 0, data.length - 1, index, e);
    }

    private void set(int treeIndex, int l, int r, int index, E e) {
        if (l == r) {
            tree[treeIndex] = e;
            return;
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if (index <= mid) {
            set(leftTreeIndex, l, mid, index, e);
        } else {
            set(rightTreeIndex, mid + 1, r, index, e);
        }
        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }


    @NonNull
    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("[");
        for (int i = 0; i < tree.length; i++) {
            if (tree[i] != null) {
                res.append(tree[i]);
            } else {
                res.append("null");
            }
            if (i != tree.length - 1) {
                res.append(",");
            }
        }
        res.append("]");
        return res.toString();
    }
}

LeetCode问题解决

307. 区域和检索 - 数组可修改
给你一个数组 nums ，请你完成两类查询。

其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right
实现 NumArray 类：

NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值 更新 为 val
int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], …, nums[right]）

使用线段树解决：

class NumArray {
    private SegmentTree<Integer> segmentTree;

    public NumArray(int[] nums) {
        if (nums.length == 0) {
            return;
        }
        Integer[] data = new Integer[nums.length];
        for (int i = 0; i < nums.length; i++) {
            data[i] = nums[i];
        }
        segmentTree = new SegmentTree<>(data, (SegmentTree.Merger<Integer>) (a, b) -> a + b);
    }


    public void update(int index, int val) {
        segmentTree.set(index,val);
    }

    public int sumRange(int left, int right) {
        return segmentTree.query(left, right);
    }
}

结语

如果以上文章对您有一点点帮助，希望您不要吝啬的点个赞加个关注，您每一次小小的举动都是我坚持写作的不懈动力！ღ( ´･ᴗ･` )