题目

输入一个整数 n ，求1～n这n个整数的十进制表示中1出现的次数。

例如，输入12，1～12这些整数中包含1 的数字有1、10、11和12，1一共出现了5次。

思路

要求出小于等于 n 的非负整数中数字 1 出现的个数。

可以假设某个四位数n = abcd，通过统计每一位上 1 出现的次数，个数上 1 出现的次数，十位上 1 出现的次数，百位 ，千位…

也就是说小于等于 n 的所有数字中，个位上出现 1 的次数 + 十位出现 1 的次数 + …，最后得到的就是总的出现次数。

比如数字13，个位上的1一共出现过2次（1和11），十位上的1一共出现过4次（10,11,12和13），那么数字1一共出现的次数为2 + 4 = 6次

通过遍历 n 的每一位得到总个数

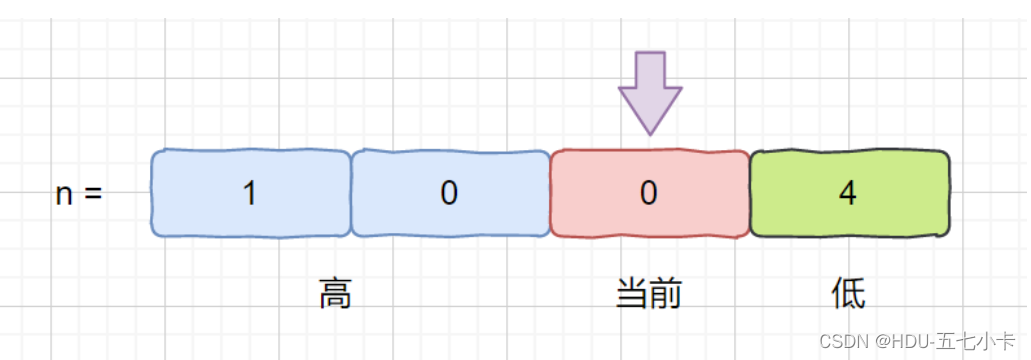
要得到十位上1出现的次数，则当前指针指向十位，称为当前位，num表示当前位的位因子，当前位为个位时 num = 1，十位时为 10，百位时为 100…同时当前位左边的定义为高位，当前位右边的定义位低位

比如n = 1004 ，此时指针指向十位（当前位）num = 10，高位为百位，千位，低位为个位

而且某一位的取值范围为 0 ~ 9,那么可以将这 10 个数分为 3 类，小于 1 （当前位数字为 0 ），等于 1（当前位数字为 1 ） ，大于 1（当前位上数字为 2 ~ 9）

这里举几个栗子：

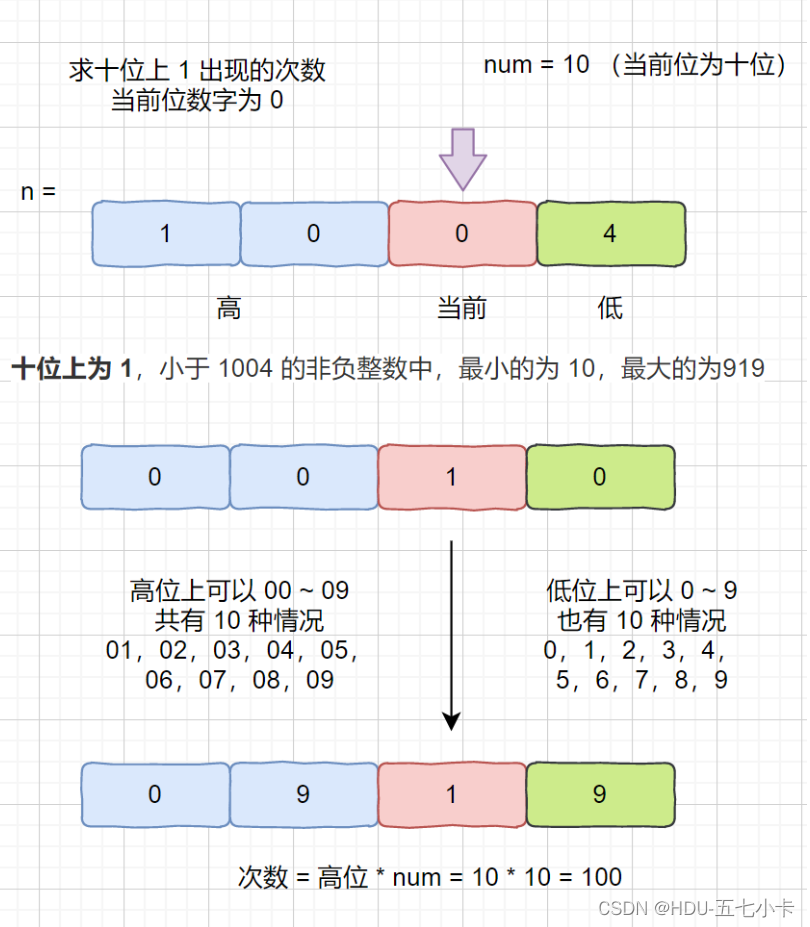
（1）n = 1004，想要计算出小于等于 1004 的非负整数中，十位上出现 1 的次数，即当前位为十位，数字为0时，小于等于 1004 的非负整数中十位上出现 1 的次数

首先进行一个判断，因为要求十位上出现1的次数，先将十位上固定为1，去调整其他位的数字（类似于滑轮密码锁，固定一位去滑动另外的数字），即十位固定为1后，小于等于1004的数字范围为10 ~ 919 （因为最小就是10，最大就是919，注意千位不可能取到1， 因为十位固定为1了，如果千位为1 ，则四位数为1X1X，必定大于1004）

（2）n = 1014，在小于等于 1014 的非负整数中，十位上为 1 的最小数字为 10，最大数字为 1014，所以需要在 10 ~ 1014 这个范围内固定住十位上的 1 ，移动其他位。

然后可以将 1014 看成是 1004 + 10 = 1014，则可以将 10 ~ 1014 拆分为两部分 0010 ~ 0919 （小于 1004的范围 ），1010 ~ 1014，相当于就是在1004的基础上多了一个低位的取值范围，即high * num + low + 1

（3）n = 1024，也就是当前位为十位，数字为 2 ~ 9 时，十位上出现 1 的次数。其中最小的为 0010，最大的为 1019，也可以将其拆成两段 0010 ~ 0919（小于1004的那部分），1010 ~ 1019（1005到1024中十位为1的那部分），此时低位取值为0~9，为num的个数（当前位为num = 10），即high * num + num

java代码如下：

class Solution{
	public int countDigitOne(int n){
		int num = 1, res = 0;//num表示位因子，因为从个位开始，所以num从1开始
		int high = n / 10, cur = n % 10, low = 0;//因为从个位开始，所以高位high为n/10，当前位cur为n%10，低位low为0
		while(high != 0 || cur != 0){//只要四位数n所有位数没有走完，则循环下去
			//对三类数字进行分类讨论
			if(cur == 0)//当前位数字为 0
				res += high * num;//对应于1004
			else if(cur == 1) //当前位数字为 1 
				res += high * num + low + 1;//多加上个位的取值，对应1014
			else  //当前位上数字为 2 ~ 9
				res += (high + 1) * num;//对应1024
			low += cur * num;
			cur = high % 10;
			high /= 10;
			num *= 10;
		}
		return res;
	}
}