同步赛链接

A-原初的信纸(最值，STL）

题意：

找 n 个数的最大值.

参考代码：

void solve() {
    int n;
    std::cin >> n;
    std::vector<int> a(n);
    for (auto &c : a)
        std::cin >> c;
    std::cout << *max_element(a.begin(), a.end()) << '\n';
}

B-骑士的对决（思维）

模拟题.(博弈)

思路：

从守卫骑士的两张牌入手，如果守卫骑士拥有 'S'  和 ‘J’，那么对于远征骑士，如果他拥有‘S’那么，出于守卫骑士已经知道远征骑士选的牌了，所以他会选择 ‘S’ ，这样就是平局，相反，如果远征骑士拥有 'J' ，那么守卫骑士必定拿出 ‘S’来战胜对方，如果远征骑士拥有 ‘B’，那么守卫骑士必定拿出 ‘J’来战胜对方，所以要么平局，要么是守卫骑士赢.剩下的两种情况参考第一种情况进行模拟即可.

参考代码：

#include <bits/stdc++.h>

//模拟

using ll = long long;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    char c;
    std::string s;
    std::cin >> s >> c;
    std::map<char, bool> mp;
    mp[s[0]] = true, mp[s[1]] = true;
    if (mp['S'] && mp['J'])
    {
        if (c == 'S') {
            std::cout << "lyrnb";
        } else {
            std::cout << "pmznb";
        } 
    } else if (mp['S'] && mp['B']) {
        if (c == 'B') {
            std::cout << "lyrnb";
        } else {
            std::cout << "pmznb";
        }
    } else {
        if (c == 'J') {
            std::cout << "lyrnb";
        } else {
            std::cout << "pmznb";
        }  
    }
    return 0;
}

C-秘密的议会（算数）

直接计算即可.

参考代码：

void solve() {
    int cnty{}, cntn{};
    std::string s;
    std::cin >> s;
    std::transform(s.begin(), s.end(), s.begin(), ::tolower);
    for (char c : s) {
        cnty += (c == 'y');
        cntn += (c == 'n');
    }
    int len = s.size();
    if (cnty >= len / 2) {
        std::cout << "pmznb\n";
    } else if (cntn >= len / 2) {
        std::cout << "lyrnb\n";
    } else {
        std::cout << "wsdd\n";
    }
}

D-城市的税金（模拟）

模拟+计算.

参考代码：

void solve() {

    int n, m;
    std::cin >> n >> m;
    std::vector<int> a(n + 1);

    for (int i = 1; i <= n; i++) {
        std::cin >> a[i];
    }

    int op, l, r;
    while (m--) {
        std::cin >> op >> l >> r;
        if (op == 1) {
            for (int i = l; i <= r; i++)
                a[i] = 1ll * a[i] * 251 % 996 * 404 * 123;
        } else {
            std::map<ll, ll> mp;
            ll max = -1;
            for (int i = l; i <= r; i++) {
                mp[a[i]]++;
            }
            for (auto it : mp) {
                max = std::max(max, it.second);
            }
            std::cout << max << '\n';
        }
    }
}

E-缺席的神官(贪心)

思路：

先把所给数组的间隔存入一个新数组，然后从小到大排序，遍历该数组到 1 ~ x-k+1，累加起来组后再加上 k 即可。

参考代码：

void solve() {
    int n, m, k;
    std::cin >> n >> m >> k;
    std::vector<int> a(n + 1), b(n + 1);
    for (int i = 1; i <= n; i++)
        std::cin >> a[i];
    for (int i = 1; i < n; i++)
        b[i] = a[i + 1] - a[i];
    std::sort(b.begin() + 1, b.end() - 1);
    ll sum = std::accumulate(b.begin() + 1, b.begin() + n + 1 - k, 0LL);
    std::cout << sum + k;
}

F-失踪的玫瑰（思维）

思路：

思维题，要求一定能找到且次数最少的方案，那么我们就要考虑最差的情况，也就是尽量不要让我们找到的情况，那么一开始的玫瑰一定在边上，可以分为四种情况：

n == 1：直接输出 1 。

n == 2：直接取两次 1 ，为了使得字典序最小，所以不取 2.

n > 2 && n % 2 == 1：例如 n == 7，最差的情况是玫瑰一开始在 7 ，然后一直在 7 和 6 徘徊，这样我们得从 2 遍历到 6 ，找到 6 的时候花在 7 的盒子上，那么我们再遍历一遍，当再次找到 6 的时候花就一定在 6 的盒子上。自己多演算几遍就知道了。为什么玫瑰一开始不在 1 上呢，为了使得字典序最小嘛！

n > 2 && n % 2 == 0：例如 n == 6，最差的情况是玫瑰一开始在 1 ，然后一直在 1 和 2 徘徊，这样我们得从 2 遍历到 5，找到 5 的时候花在 2 的盒子上，然后再从 5 找到 2，找到 2 的时候就一定能找到花了。

其实以上的思路就是通过紧逼，一次不行就再来一次，从而使得一定可以找到花。

参考代码：

void solve() {
    int n;
    std::cin >> n;
    if (n & 1) {
        for (int i = 2; i < n; i++)
            std::cout << i << " ";
        for (int i = 2; i < n; i++)
            std::cout << i << ' ';
    } else {
        for (int i = 2; i < n; i++)
            std::cout << i << " ";
        for (int i = n - 1; i >= 2; i--)
            std::cout << i << ' ';
    }
    std::cout << '\n';
}

G-虚数的纸牌(模拟)

参考代码：

int change(char s) {
    if (s >= '3' && s <= '9')
        return s - '0';
    if (s == '0')
        return 10;
    if (s == 'J')
        return 11;
    if (s == 'Q')
        return 12;
    if (s == 'K')
        return 13;
    if (s == 'A')
        return 14;
    if (s == '2')
        return 15;
}

void solve() {
    std::string s;
    std::cin >> s;
    int res = s.size(); // 单
    int cnt[16] = {0};
    for (char c:s) {
        cnt[change(c)]++; // 出现次数
    }
    for (int i = 3; i <= 15; i++) {
        if (cnt[i] >= 2)
            res += 1ll * cnt[i] * (cnt[i] - 1) / 2; // 对子
        if (cnt[i] == 4) {
            res++;                     // 炸弹
            res += 4 * (s.size() - 4); // 三带一,减去自己的4张
            for (int j = 3; j <= 15; j++) {
                if (i != j) {
                    res += 4ll * cnt[j] * (cnt[j] - 1) / 2; // 三带二
                }
            }  
        }
        else if (cnt[i] == 3) {
            res += s.size() - 3; // 三带一
            for (int j = 3; j <= 15; j++) {
                if (i != j) {
                    res += 1ll * cnt[j] * (cnt[j] - 1) / 2; // 三带二
                }
            }
                
        }
        if (i <= 11) {
            int t = 1;
            for (int j = 0; j < 5; ++j) // 五单顺子
                t *= cnt[i + j];
            res += t;
        }
    }
    std::cout << res << '\n';
}

H-绵羊的银币（思维）

思路：

这道题以 2 的幂次方从为区间不断递增，区间内都是一个相同的数，且区间其实就是斐波那契数列，所以只需要知道 n 是属于哪一个区间即可。 

参考代码：

#include <bits/stdc++.h>

using ll = long long;

ll f[99];

void solve() {
    ll p = 1, x = 0, n;
    std::cin >> n;
    while (p <= n)
        p <<= 1, x++;
    std::cout << f[x - 1] << '\n';
}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int t;
    std::cin >> t;
    f[0] = f[1] = 1;
    for (int i = 2; i <= 90; i++)  //初始化
        f[i] = f[i - 1] + f[i - 2];
    while (t--) {
        solve();
    }
    return 0;
}

I-迷途的怪物(思维)

如果 n 是奇数的话，（p -1）^ n 对 p 取模，结果还是 p - 1；如果是偶数的话，结果就是 1.

参考代码：

void solve() {
    std::string s;
    int p;
    std::cin >> p >> s;
	if ((s.back()-'0') & 1) {
        std::cout << p - 1 << '\n';
    } else {
        std::cout << "1\n";
    }
}

J-简单的数学（数学题）

参考代码：

void solve() {
    int n;
    std::cin >> n;
    if (n & 1) {
        std::cout << 1ll * (n + 1) * n << '\n';
    } else {
        std::cout << 1ll * (n + 1) * n * (-1) << '\n';
    }
}

K-消亡的质数（思维，数学）

思路：

立方差公式为 p = a^3 - b^3 = (a - b) (a^2 + ab + b^2)，两个数的乘积本来应该是合数，但 p 确实质数，说明两个乘数中有一个为 1，可想而知 a - b = 1，那么 p = a^2 + a*b + b^2，题目就变得简单了，只要枚举判断是否存在这样相邻的两个数的立方差等于 p。

参考代码：

#include <bits/stdc++.h>

using ll = long long;

ll judge(ll x) {
    if (x <= 0)
        return 0;
    for (ll i = 1; i * i + i * (i + 1) + (i + 1) * (i + 1) <= x; i++) {
        if (i * i + i * (i + 1) + (i + 1) * (i + 1) == x) {
            return 1;
        }
    } 
    return 0;
}
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int t;
    std::cin >> t;
    while (t--) {
        ll p;
        std::cin >> p;
        std::cout << (judge(p) ? "YES\n" : "NO\n");
    }
    return 0;
}

L-危险的台阶（思维）

我首先想的是从最高（外）处那块石板开始考虑，假设每块石板的长度为1。当只有一块石阶时，显然，由于石板密度均匀，一块长度为1的石板的重心即为1/2，因此，最大伸出长度为1/2。然后，考虑两块石板时的情况，如下图。只需找到两块石板的重心即可，显然可得，最大长度为1/2+1/4=3/4。结果应是 （1/2）L+（1/4）L+（1/6）L+…+（1/2n）L（可根据重心联立方程组解得第三块石板伸出长度为1/6).

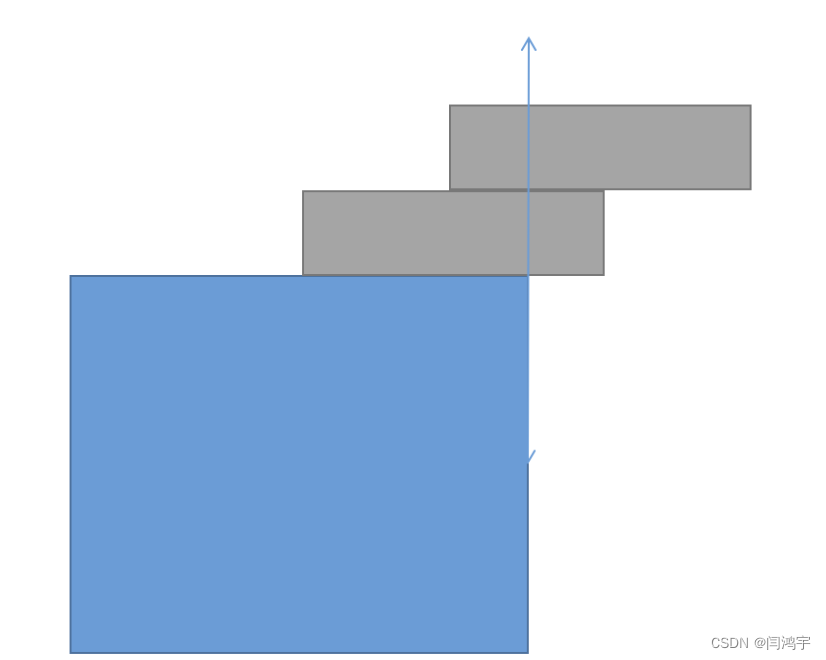参考代码：

#include <bits/stdc++.h>

using ll = long long;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    ll n, l, m;
    std::cin >> n >> l >> m;
    double sum = 0,s = 2;
    int i = 1;
    while (n--) {
        sum += l / (s * i++);
    }
    std::cout << std::fixed << std::setprecision(4) << sum;
    return 0;
}

M-破碎的愿望（思维，STL）

思路：

该题数很大，要定义为长整型。由于字符串变化都是把字符串翻转后接到原字符串后面无限延伸，所以无限延伸的字符串只不过是所给字符串翻转后接到所给字符串得到的新字符串为循环节一直循环增加。我们只需要把 k 对所得到循环节字符串长度取余后输出相应位置的字符。

注意： 有一个特判，如果取余后为 0，说明是最后一个字符。

参考代码：

#include <bits/stdc++.h>

using ll = long long;

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    ll n, k;
    std::string s;
    std::cin >> n >> k >> s;
    ll x = k % (n * 2);
    std::string s1 = s;
    std::reverse(s1.begin(), s1.end());
    s = s + s1;
    if (x == 0) {
        std::cout << s[n * 2 - 1];
    } else {
        std::cout << s[x - 1];
    }
    return 0;
}