相关文章
- K近邻算法和KD树详细介绍及其原理详解
- 朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解
文章目录
- 相关文章
- 前言
- 一、朴素贝叶斯算法
- 二、拉普拉斯平滑
- 总结
前言
今天给大家带来的主要内容包括:朴素贝叶斯算法、拉普拉斯平滑。这些内容也是机器学习的基础内容,本文不全是严格的数学定义,也包括生动的例子,所以学起来不会枯燥。下面就是本文的全部内容了!
一、朴素贝叶斯算法
现在有这样一个例子,大学生小明是班级里最受欢迎的同学,有一天老师布置的题目非常难,于是小明给班级里面的30个同学群发求助消息:
由于小明的人缘很好,收到消息的同学均纷纷回复小明,但是小明发现这30个回复里面既有作业答案,同时也意外收获了深情的告白。小明可以分辨出有16份作业答案,还有13份情书,唯独班长的回复小明没有看懂:

于是小明想,可不可以按照消息中出现的关键词来给班长的回复分一下类,看看班长的回复是作业答案还是情书:

小明首先根据收到的消息计算任何一则消息是作业答案还是情书的概率:

然后从所有的消息中选定了四个关键词作为分类依据,并记录下每一个词在作业答案和情书中出现的次数:

随后小明在两种情况下分别计算关键词出现的概率,例如在作业答案消息中,“喜欢”这个词一共出现了3次,而所有关键词出现了15次,所以在作业答案消息中出现“喜欢”这个词的概率是 3 15 \frac{3}{15} 153,以此类推,可以得到所有关键词在两种不同消息中出现的概率:
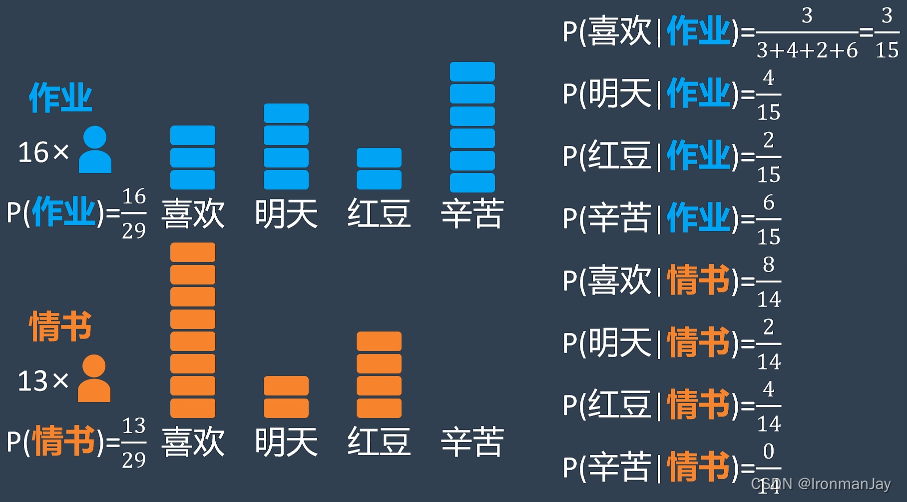
当我们计算得到所有关键词在两种不同消息中出现的概率后,再来分析班长的回复,假设班长给小明发的消息中包含“红豆”和“喜欢”两个关键词,首先我们先假设这是一份作业,然后再乘以作业中出现“红豆”和“喜欢”两个关键词的概率:

这个公式的计算结果可以理解为猜测这是一份作业的正确程度,代入数据可以计算得到:

同样可以计算假设这是一份情书的正确程度:

很明显,小明收到的班长的信息可能为情书的概率要比可能为作业答案的概率要高,所以小明得出结论,原来班长发的是一封情书:

以上整个过程就是我们常说的朴素贝叶斯算法,在朴素贝叶斯算法中,假设两个特征维度之间是相互独立的,在刚才的例子中,认为两个关键词是相互独立的,也就是说他们出现的顺序和上下文关系并不影响计算结果,哪怕它们表达的意思天差地别也不会有任何影响:

但是在现实情况中很少有相互独立的情况发生,大多都是有关联的,所以维度之间相互独立的假设就显得太过于简单粗暴,那么这种算法就被称为朴素贝叶斯算法,刚刚通过文字和例子给大家直观介绍了什么是朴素贝叶斯算法,下面让我们从数学角度总结一下朴素贝叶斯算法。
现在假设给定一个数据集
T
T
T,其中包含:
T
=
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
…
,
(
x
n
,
y
n
)
T={(x_{1},y_{1}),(x_{2},y_{2}),\dots,(x_{n},y_{n})}
T=(x1,y1),(x2,y2),…,(xn,yn)
对于其中的参数需要注意其含义:
- x i = ( x 1 , … , x n ) x_{i}=(x^{1},\dots,x^{n}) xi=(x1,…,xn), x i ( 1 ≤ x ≤ n ) x_{i}(1≤x≤n) xi(1≤x≤n)是样本特征,由一系列独立的特征维度构成
- y i = c k y_{i}=c_{k} yi=ck, y i ( 1 ≤ y ≤ n ) y_{i}(1≤y≤n) yi(1≤y≤n)是样本类别, y i y_{i} yi可能属于 c i ( 1 ≤ i ≤ k ) c_{i}(1≤i≤k) ci(1≤i≤k)中的任何一个
刚才我们已经介绍过了,朴素贝叶斯算法就是基于样本特征
x
x
x来预测样本属于的类别
y
y
y。根据贝叶斯定理,我们可以得到这样一个看似复杂的等式:
P
(
y
=
c
k
∣
x
)
=
P
(
y
=
c
k
)
P
(
x
∣
y
=
c
k
)
∑
k
P
(
y
=
c
k
)
P
(
x
∣
y
=
c
k
)
P\left(y=c_{k} \mid x\right)=\frac{P\left(y=c_{k}\right) P\left(x \mid y=c_{k}\right)}{\sum_{k} P\left(y=c_{k}\right) P\left(x \mid y=c_{k}\right)}
P(y=ck∣x)=∑kP(y=ck)P(x∣y=ck)P(y=ck)P(x∣y=ck)
在上式中,因为分母上的每一个值对每一个类别来说都是一样的,所以我们可以将上式简化一下,得到一个正比关系:
P
(
y
=
c
k
∣
x
)
∝
P
(
y
=
c
k
)
P
(
x
∣
y
=
c
k
)
P\left(y=c_{k} \mid x\right) \propto P\left(y=c_{k}\right) P\left(x \mid y=c_{k}\right)
P(y=ck∣x)∝P(y=ck)P(x∣y=ck)
在上式中,
y
y
y就是可能被分类的类别,也就是刚才例子中的作业答案或者情书,而
x
x
x就是关键词的集合。因为我们假设
x
x
x的特征是相互独立的,所以可以把它们拆分成一系列条件概率的相乘:
P
(
y
=
c
k
∣
x
)
∝
P
(
y
=
c
k
)
∏
j
P
(
x
j
∣
y
=
c
k
)
P\left(y=c_{k} \mid x\right) \propto P\left(y=c_{k}\right) \prod_{j} P\left(x^{j} \mid y=c_{k}\right)
P(y=ck∣x)∝P(y=ck)j∏P(xj∣y=ck)
通过上式就可以在例子中计算分类正确的概率,最后选择正确分类概率最高的类别作为分类结果即可,这就是朴素贝叶斯法的数学形式。
二、拉普拉斯平滑
我们再来看另一个例子,假设有一段话是这样写的:

我们现在要判断它是作业答案还是情书,那么还是按照上面介绍的朴素贝叶斯算法来计算它们的正确程度:

因为“喜欢”这个词出现了三次,所以需要乘三次,也就是为什么需要计算三次方。并且情书中并没有“辛苦”这个关键词出现过,所以“辛苦”在情书中出现的概率为0,所以导致最后判断其为情书的概率为0,算法从而将这段信息判断为作业答案。
很明显这样是不对的,我们人类可以很轻松的判断出这是一份情书,但是计算机使用算法计算是死的,并没有人类的情感。出现上面那种情况的原因是什么呢?是因为“辛苦”在情书中出现的概率为0,从而导致最后的计算结果为0,为了解决这个问题,我们可以使用拉普拉斯平滑技巧。
拉普拉斯平滑技巧就是在每个关键词上面人为增加一个出现的次数,这样就可以保证每一项都不为0:

按照拉普拉斯平滑后的次数,我们可以重新计算每个关键词出现的频率:

当我们使用平滑后的结果,再计算时就可以得到正确的结论了:

总结
以上就是本文的全部内容了,这个系列还会继续更新,给大家带来更多的关于机器学习方面的算法和知识,下篇博客见!