DS期末复习卷（四）

news2024/9/23 7:26:33

一、选择题(每题1分共 20分)

1．设一维数组中有n个数组元素，则读取第i个数组元素的平均时间复杂度为（C ）。
(A) O(n) (B) O(nlog2n) © O(1) (D) O(n2)

数组读取元素的时间复杂度为O（1）

2．设一棵二叉树的深度为k，则该二叉树中最多有（ D）个结点。
(A) 2k-1 (B) 2^k ( C) 2 ^(k-1) ( D ) 2 ^k-1

满二叉树用等比数列求和公式算出即为D

3．设某无向图中有n个顶点e条边，则该无向图中所有顶点的入度之和为（ D ）。
(A) n (B) e © 2n (D) 2e

无向图中入度之和等于出度之和等于二倍的边数

4．在二叉排序树中插入一个结点的时间复杂度为（ B ）。
(A) O(1) (B) O(n) © O(log2n) (D) O(n2)

平衡二叉树，若深度不平衡，类似于单链表，时间复杂度为o(n);
深度平衡的情况下，时间复杂度为o(logn);

5．设某有向图的邻接表中有n个表头结点和m个表结点，则该图中有（ C ）条有向边。
(A) n (B) n-1 © m (D) m-1

在有向图的邻接表中表头结点的个数即为顶点个数，表结点的个数即为边的条数

6．设一组初始记录关键字序列为(345，253，674，924，627)，则用基数排序需要进行（ A ）趟的分配和回收才能使得初始关键字序列变成有序序列。
(A) 3 (B) 4 © 5 (D) 8

要分别按照个位十位百位进行排序

7．设用链表作为栈的存储结构则退栈操作（ B ）。
(A) 必须判别栈是否为满 (B) 必须判别栈是否为空
© 判别栈元素的类型 (D) 对栈不作任何判别

只有栈中有元素时才能出栈所以要判断是否栈空

8．下列四种排序中（ A ）的空间复杂度最大。
(A) 快速排序 (B) 冒泡排序 © 希尔排序 (D) 堆

9．设某二叉树中度数为0的结点数为N0，度数为1的结点数为Nl，度数为2的结点数为N2，则下列等式成立的是（ C ）。
(A) N0=N1+1 (B) N0=Nl+N2 © N0=N2+1 (D) N0=2N1+l

10.设有序顺序表中有n个数据元素，则利用二分查找法查找数据元素X的最多比较次数不超过（ A）。
(A) log2n+1 (B) log2n-1 © log2n (D) log2(n+1)

向上取整

二、填空题(每空1分共 20分)

1．设有n个无序的记录关键字，则直接插入排序的时间复杂度为________，快速排序的平均时间复杂度为_________。

o(n^2) O(nlong2n)

2．设指针变量p指向双向循环链表中的结点X，则删除结点X需要执行的语句序列为_______ _________________________（设结点中的两个指针域分别为llink和rlink）。

p>llink->rlink=p->rlink;p->rlink->llink=p->rlink

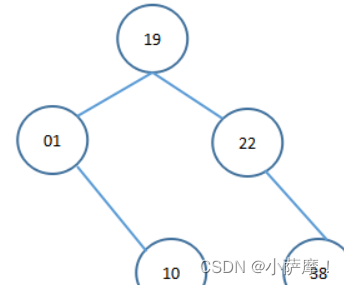
3．根据初始关键字序列(19，22，01，38，10)建立的二叉排序树的高度为___________。

3

4．深度为k的完全二叉树中最少有____________个结点。

2^k-1

5．设初始记录关键字序列为(K1，K2，…，Kn)，则用筛选法思想建堆必须从第______个元素开始进行筛选。

“…我们称这个自堆至叶子的调整过程为筛选。从一个无序序列建堆过程就是一个反复筛选的过程。若将此序列看成是一个完全二叉树，则最后一个非终端结点是第[n/2]个元素，由此筛选只需从第[n/2]个元素开始” 出自严蔚敏《数据结构》280页。

6．设哈夫曼树中共有99个结点，则该树中有________个叶子结点；若采用二叉链表作为存储结构，则该树中有____个空指针域。

50 100
N0+N2=99 N0=1+N2 N0=50 N2=49

7．设有一个顺序循环队列中有M个存储单元，则该循环队列中最多能够存储________个队列元素；当前实际存储________________个队列元素（设头指针F指向当前队头元素的前一个位置，尾指针指向当前队尾元素的位置）。

m-1 (R-F+M)%M
规定循环队列最多只能有MaxSize-1个队列元素，当循环队列中只剩下一个空存储单元时，队列就已经满了。因此，队列判空的条件是front=rear，而队列判满的条件是front=（rear+1)%MaxSize

8．设顺序线性表中有n个数据元素，则第i个位置上插入一个数据元素需要移动表中_______个数据元素；删除第i个位置上的数据元素需要移动表中_______个元素。

n-i+1 n-i

9．设一组初始记录关键字序列为(20，18，22，16，30，19)，则以20为中轴的一趟快速排序结果为______________________________。

(19，18，16，20，30，22)

10．设一组初始记录关键字序列为(20，18，22，16，30，19)，则根据这些初始关键字序列建成的初始堆为________________________。

(16，18，19，20，30，22)

11．设某无向图G中有n个顶点，用邻接矩阵A作为该图的存储结构，则顶点i和顶点j互为邻接点的条件是___ A[i][j]=1__________________。

12．设无向图对应的邻接矩阵为A，则A中第i行上非0元素的个数_________第i列上非0元素的个数（填等于，大于或小于）。

等于无向图的邻接矩阵关于对角线对称

13．设前序遍历某二叉树的序列为ABCD，中序遍历该二叉树的序列为BADC，则后序遍历该二叉树的序列为_____________。

BDCA

14．设散列函数H(k)=k mod p，解决冲突的方法为链地址法。要求在下列算法划线处填上正确的语句完成在散列表hashtalbe中查找关键字值等于k的结点，成功时返回指向关键字的指针，不成功时返回标志0。

typedef struct node {int key;struct node *next;} lklist;

void createlkhash(lklist*hashtable[ ])

{

int i,k;  lklist *s;

for(i=0;i<m;i++)_____________________;

for(i=0;i<n;i++)

{

s=(lklist*)malloc(sizeof(lklist)); s->key=a[i];

k=a[i] % p;s->next=hashtable[k];_______________________;

}

}

hashtable[i]=0，hashtable[k]=s

三、计算题(每题10分，共30分)

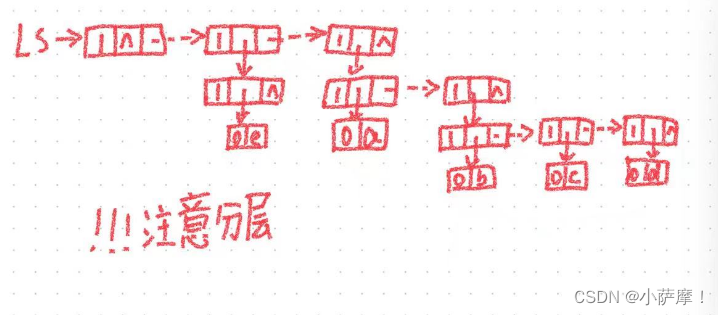
1、画出广义表LS=(( ) , (e) , (a , (b , c , d )))的头尾链表存储结构。

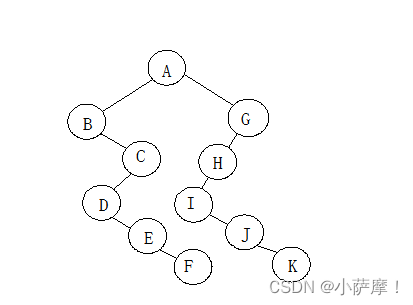
2、下图所示的森林：　　
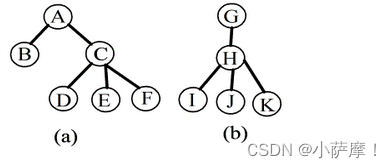
在这里插入图片描述

(1) 求树（a）的先根序列和后根序列；

先序：ABCDEF
后序：BDEFCA

(2) 求森林先序序列和中序序列；

先序：ABCDEFGHIJK
中序：BDEFCAIJKHG

（3）将此森林转换为相应的二叉树；

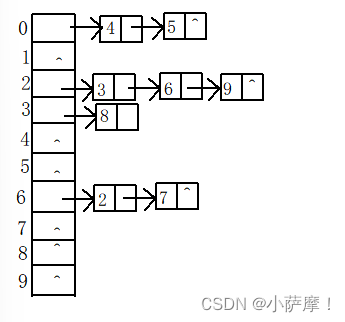
3、设散列表的地址范围是[ 0…9 ]，散列函数为H（key）= （key ^2 +2）MOD 9,并采用链表处理冲突，请画出元素7、4、5、3、6、2、8、9依次插入散列表的存储结构。

H(4)=H(5)=0,H(3)=H(6)=H(9)=2,H(8)=3,H(2)=H(7)=6

四、算法设计题(每题10分，共30分)

设单链表中有仅三类字符的数据元素(大写字母、数字和其它字符)，要求利用原单链表中结点空间设计出三个单链表的算法，使每个单链表只包含同类字符。

typedef char datatype;
typedef struct node {
datatype data; 
struct node *next;
}lklist;
void split(lklist *head,lklist *&ha,lklist *&hb,lklist *&hc)
{
   lklist *p; 
   ha=0,hb=0,hc=0;
   for(p=head;p!=0;p=head)
   {
    head=p->next; 
    p->next=0;
    if (p->data>='A' && p->data<='Z') {p->next=ha; ha=p;}
    else if (p->data>='0' && p->data<='9') {p->next=hb; hb=p;}
    else {p->next=hc; hc=p;}
   }
}

2.设计在链式存储结构上交换二叉树中所有结点左右子树的算法。

typedef struct node {
int data; 
struct node *lchild,*rchild;
} bitree;
void swapbitree(bitree *bt)
{
   bitree *p;
   if(bt==0) return;
	swapbitree(bt->lchild); 
	swapbitree(bt->rchild);
	p=bt->lchild; 
	bt->lchild=bt->rchild; 
	bt->rchild=p;
}

3.在链式存储结构上建立一棵二叉排序树。

#define n 10
typedef struct node{
int key; 
struct node *lchild,*rchild;
}bitree;
void bstinsert(bitree *&bt,int key)
{
   if (bt==0){
   bt=(bitree *)malloc(sizeof(bitree));   
   bt->key=key;
   bt->lchild=bt->rchild=0;}
   else if (bt->key>key) 
   	bstinsert(bt->lchild,key); 
   	else 
   	bstinsert(bt->rchild,key);
}
void createbsttree(bitree *&bt)
{
   int i;
   for(i=1;i<=n;i++) 
   bstinsert(bt,random(100));
}