文章目录
- 二分问题常规解法:
- 使用C++STL自带算法解决二分问题:
- 小数二分
二分问题常规解法:
二分问题注意事项:
-
题目可能无解,但二分一定有解(也就是二分问题会得到一个结果,但是该结果可能不符合题目要求)
-
有单调性的一定可以二分,可以二分的题目不一定有单调性,二分和单调性无关
-
二分的本质是边界:找到一个性质可以把区间一分为二
视频推荐(强烈推荐看一遍):二分查找为什么总是写错?_哔哩哔哩_bilibili
二分模板:
int left = -1, right = nums.size();
int mid = 0;
while (left + 1 != right)
{
mid = (left + right) / 2;
if (IsBlue(mid)) left = m; //IsBlue表示mid是否满足蓝色区间的性质
else r = m;
}
if (left != -1) //如果不存在满足蓝色区间的数值
{
}
if (right != nums.size())//如果不存在满足红色区间的数值
{
}
使用思路如下:
- 建模:划分蓝红区域,确定IsBlue()—左半边的性质
- 确定最后使用的是left还是right
- 套用算法模板
m始终处于[0,N)
mid=(left+right)/2
知道left的最小值是-1,right的最小值是1(如果是0,则不满足left+1!=right则不会进入循环),所以mid最小是0
知道right的最大值是N,left的最大值是N-2(N-1的话就不满足left+1!=right则不会进入循环),所以mid最大值是N-1
例题练习:
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
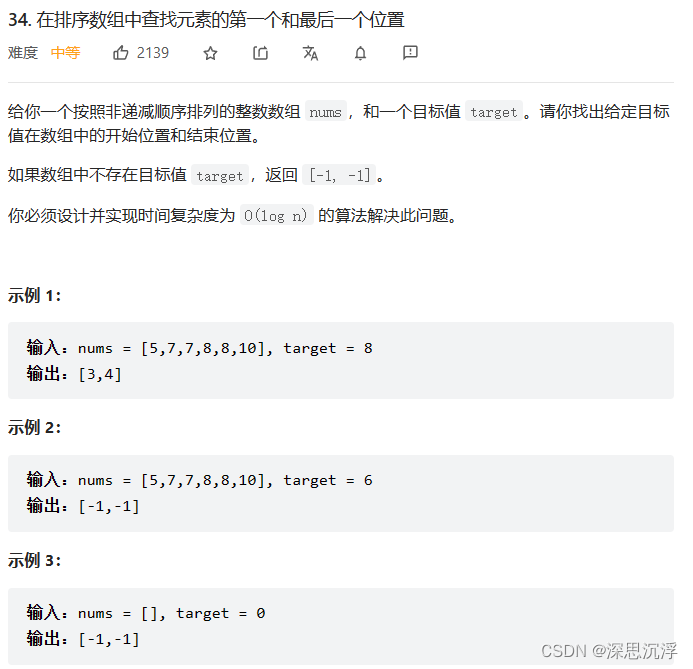
解法:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target)
{
vector<int> res;
int begin = -1, end = -1;//一连串目标值的第一个目标值,例如target = 3,3 3 3 begin是第一个3的下标,end是最后一个3的下标
int left = -1, right = nums.size();
int mid = 0;
while (left + 1 != right)
{
mid = (left + right) / 2;
if (nums[mid] < target) left = mid;
else right = mid;
}
if (right != nums.size() && nums[right] == target)//如果存在右边的区间且right等于目标值,则right是begin
{
begin = right;
}
else//说明区间不存在目标值
{
res.push_back(begin);
res.push_back(end);
return res;
}
left = -1, right = nums.size();
mid = 0;
while (left + 1 != right)
{
mid = (left + right) / 2;
if (nums[mid] <= target) left = mid;
else right = mid;
}
end = left;
res.push_back(begin);
res.push_back(end);
return res;
}
};
使用C++STL自带算法解决二分问题:
std::lower_bound()返回大于等于value值的第一个元素的迭代器
std::upper_bound()返回大于等于value值的最后一个元素的迭代器
使用STL算法解决上述问题
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
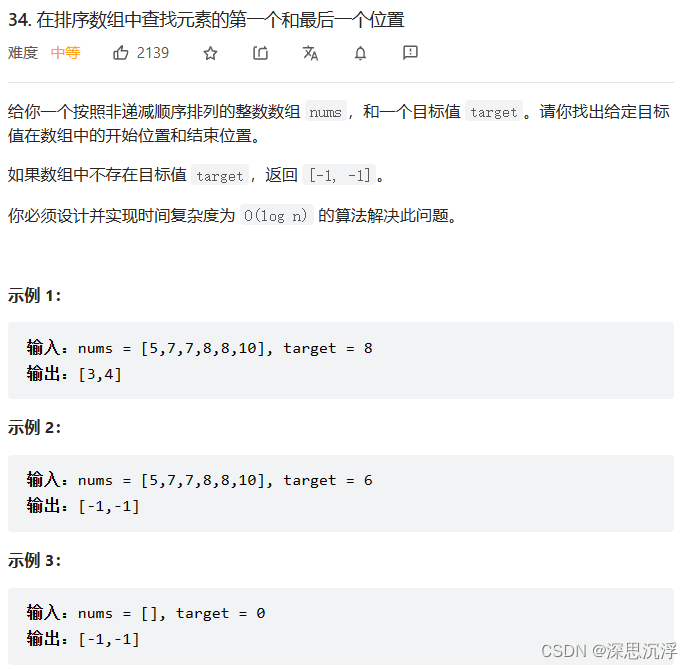
class Solution
{
public:
vector<int> searchRange(vector<int>& nums, int target)
{
vector<int> ans = {-1, -1};
//查找第一个大于或等于target的元素的迭代器
auto it_begin = lower_bound(nums.begin(), nums.end(), target);
//如果找到且等于target
if(it_begin != nums.end() && *it_begin == target)
ans[0] = it_begin - nums.begin();
//查找第一个大于target的元素的迭代器
auto it_end = upper_bound(nums.begin(), nums.end(), target);
//当nums只有一个元素时且大于或等于target时,it_end肯定会指向nums.end()
//小于时,nums.begin() == it_end,此时返回-1
if(it_end != nums.begin() && *(it_end - 1) == target)
ans[1] = it_end - nums.begin() - 1;
return ans;
}
};
小数二分
小数二分是和整数二分区别是精度,小数二分需要通过精度来判断是否退出循环
790. 数的三次方根 - AcWing题库

#include<iostream>
#include<iomanip>
using namespace std;
double searchnumber(double n)
{
bool isre = false;
if (n < 0)
{
n = -n;
isre = true;
}
double l = 0, r = 0;
if (n < 1)
r = 1;
else
r = n;
double mid = 0;
while (r - l > 1e-8)
{
mid = (l + r) / 2;
if ((mid * mid * mid) >= n) r = mid;
else l = mid;
}
if (!isre)
return mid;
else
return -mid;
}
int main()
{
double n = 0;
cin >> n;
cout << fixed<<setprecision(6)<<searchnumber(n) << endl;//sixed<<setprecision(6)控制输出几位小数
return 0;
}
这里面1e-8为精度,数值越小最后得到的三次方根越准确