前言：内容包括四大模块：题目，代码实现，大致思路，代码解读

题目：

描述

给定一个长度为n的数组nums，请你找到峰值并返回其索引。数组可能包含多个峰值，在这种情况下，返回任何一个所在位置即可。

1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于

2.假设 nums[-1] = nums[n] = −∞

3.对于所有有效的 i 都有 nums[i] != nums[i + 1]

4.你可以使用O(logN)的时间复杂度实现此问题吗？

如输入[2,4,1,2,7,8,4]时，会形成两个山峰，一个是索引为1，峰值为4的山峰，另一个是索引为5，峰值为8的山峰，如下图所示：

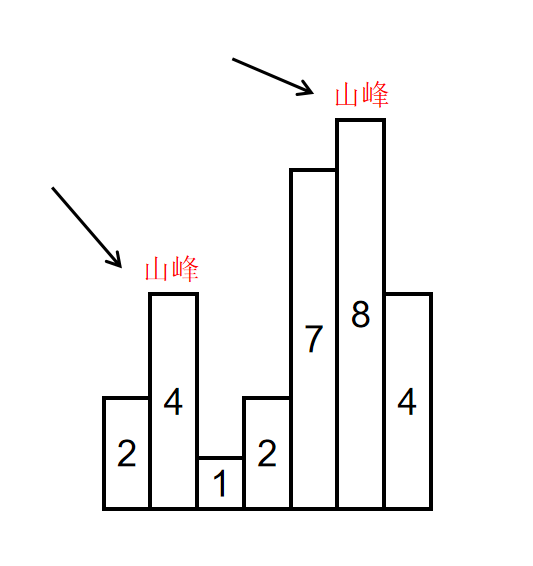
示例1

输入：

[2,4,1,2,7,8,4]

返回值：

1

说明：

4和8都是峰值元素，返回4的索引1或者8的索引5都可以     

示例2

输入：

[1,2,3,1]

返回值：

2

说明：

3 是峰值元素，返回其索引 2    

代码实现：

 

int findPeakElement(int* nums, int numsLen ) 
{
    // write code here
    if(numsLen==1 || nums[0]>nums[1])
    {
        return 0;
    }
    if(nums[numsLen-1]>nums[numsLen-2])
    {
        return numsLen-1;
    }
    int left = 0;
    int right = numsLen-1;
    int mid = 0;
    while(left<right)
    {
        mid=left+(right-left)/2;
        if(nums[mid]>nums[mid+1])
        {
            right=mid;
        }
        else
        {
            left=mid+1;
        }
    }
    return left;
}

大致思路：

采用二分查找

初始化：left作为第一个元素的下标，left=0

               right作为最后一个元素的下标，right=元素个数-1

1 中间值比右边大，认为是向左递增的，则要使得范围向左边靠，right=mid

注意：不要right=mid-1，因为mid下标的值也有可能是峰值

2. 中间值比右边小，认为是开始递减了，则要使得范围向右边靠，left=mid+1

    直至left不再小于right，则left下标的值即是峰值

示例：int arr[] = {3, 5, 4, 4, 3, 2, 1}

left=0,right=6,mid=3: arr[3]=4 > arr[4]=3, 则right = mid = 3; 从右往左是递增的
left=0,right=3,mid=1: arr[1]=5 > arr[2]=4, 则right = mid = 1; 从右往左是递增的
left=0,right=1,mid=0: arr[0]=3 < arr[1]=5, 则left = mid + 1 = 1; 从右往左开始递降了

此时left=1，right=1，left不再小于right，循环停止，找到了峰值5，返回下标left

注意：循环的条件不能是left<=right，以如上数组为例：此时已经找到峰值5，left=right=1，若是循环条件是left<=right，则还会进入循环，进行二分查找：

        mid=left+(right-left)/2;
        if(nums[mid]>nums[mid+1])
        {
            right=mid;
        }

满足以上条件，进入if语句，right=mid=1，再去判断部分left<=right的，则又重复以上逻辑

死循环

代码解读：

part 1：处理边界情况

    if(numsLen==1 || nums[0]>nums[1])
    {
        return 0;
    }
    if(nums[numsLen-1]>nums[numsLen-2])
    {
        return numsLen-1;
    }

若是数组只有一个元素or数组的第一个元素>第二个元素

则下标为0的值是峰值，因为题目告知： nums[-1] = nums[n] = −∞

part 2：二分查找峰值

    int left = 0;
    int right = numsLen-1;
    int mid = 0;
    while(left<right)
    {
        mid=left+(right-left)/2;
        if(nums[mid]>nums[mid+1])
        {
            right=mid;
        }
        else
        {
            left=mid+1;
        }
    }
    return left;

定义下标left和right，left开始是第一个元素的下标，right开始是最后一个元素的下标

若是中间值>右边，则认为是从右向左递增，故而我们使范围向左边靠，right=mid

若是中间值<右边，则认为从右向左开始递减了，故而峰值出现在右边，范围要向右边靠，left=mid+1

直至某一次循环中left不再小于right，则说明找到了峰值，结束了循环，返回left的下标