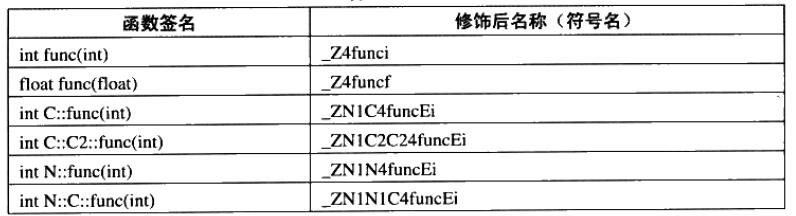
传送门

6354. 找出数组的串联值

题目

---

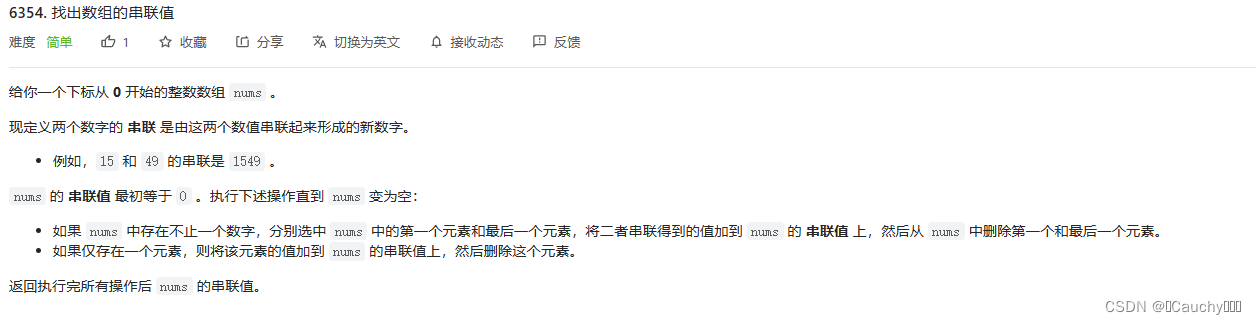
思路

前后指针

---

代码

class Solution {
public:
    long long findTheArrayConcVal(vector<int>& nums) {
        long long res = 0;
        int n = nums.size();
        for (int i = 0, j = n - 1; i < j; i++, j--) {
            res += stol(to_string(nums[i]) + to_string(nums[j]));
        }
        if (n & 1) res += nums[n / 2];
        return res; 
    }
};

---

6355. 统计公平数对的数目

题目

---

思路

$lower<=nums[i]+nums[j]<=upper$

转化：

$lower-nums[i]<=nums[j]<=upper-nums[i]$

倒序遍历，动态查找后缀的在区间如上范围内的值的个数。那么考虑用树状数组获取区间内值的个数。

由于范围过大，且做差会造成负数，树状数组下标从1开始。所以换用map的树状数组，平且值向右平移到正数。

---

代码

class Solution {
public:
    using ll = long long;
    static constexpr ll N = 2e9 + 7;
    class BIT {
    public:
        BIT() {}
        unordered_map<ll, int> tr;
        void add(ll x, int v = 1) { for (; x < N << 1; x += x & -x) tr[x] += v; }
        ll sum(ll x) { ll res = 0; for (; x; x -= x & -x) res += tr[x]; return res; }
    }; // 切记用 BIT tr; tr.add(); tr.sum();
    long long countFairPairs(vector<int>& a, int L, int R) {
        ll res = 0;
        BIT tree;
        for (int i = a.size() - 1; i >= 0; i--) {
            res += tree.sum(R - a[i] + N) - tree.sum(L - a[i] - 1 + N);
            tree.add(a[i] + N);
        }
        return res;
    }
};

---

6356. 子字符串异或查询

题目

---

思路

映射数值对应的最小开始下标即可，数值在1e9，并且无前导 ‘0’，所以只需要 O(30n)。

---

代码

class Solution {
public:
    vector<vector<int>> substringXorQueries(string s, vector<vector<int>>& q) {
        vector<vector<int>> res;
        
        map<int, int> mp;
        int mn = 1e9;
        for (int i = 0; i < s.size(); i++) {
            int x = 0;
            for (int j = 0; j < 31 && i + j < s.size(); j++) {
                if (s[i + j] - '0' == 0 && x == 0) {
                    mn = min(mn, i);
                    break;
                }
                x = x * 2 + s[i + j] - '0';
                if (mp.count(x)) {
                    mp[x] = min(mp[x], i);
                } else {
                    mp[x] = i;
                }
            }
        }
        for (int i = 0; i < q.size(); i++) {
            int x = q[i][0] ^ q[i][1];
            int y = x;
            int cnt = 0;
            while (y) { cnt++; y /= 2; }
            
            vector<int> v{-1, -1};
            if (cnt == 0 && mn != 1e9) {
                v[0] = mn;
                v[1] = mn;
            }
            if (mp.count(x)) {
                v[0] = mp[x];
                v[1] = v[0] + cnt - 1;
            }
            res.push_back(v);
        }
        
        return res;
    }
};

---

6357. 最少得分子序列

题目

---

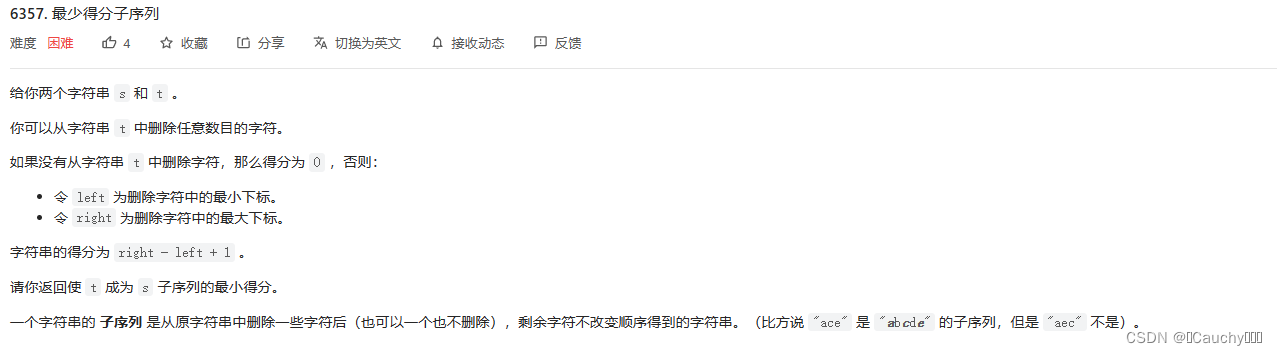
思路

维护前后缀数组，$l[i],r[i]$：表示字符串 $s$ 的前 $i$ 位子序列在字符串 $t$ 中匹配的最长前缀。$r$ 同理最长后缀。

---

代码

class Solution {
public:
    int minimumScore(string s, string t) {
        int n = s.size(); 
        vector<int> l(n, 0), r(n, 0); 
        int j = 0;
        for (int i = 0; i < s.size(); i++) {
            if (j < t.size() && s[i] == t[j]) ++j;
            l[i] = j;
        }

        j = t.size() - 1;
        for (int i = s.size() - 1; i >= 0; i--) {
            if (j >= 0 && s[i] == t[j]) --j;
            r[i] = t.size() - j - 1;
        }

        int res = 1e9; 
        for (int i = 0; i < n - 1; i++) {
            int L = l[i], R = r[i + 1];
            if (L + R >= t.size()) return 0; // 都能匹配上，说明t本就是s的子序列
            res = min(res, (int)((t.size() - R - 1) - (L) + 1));
        }
        res = min(res, (int)t.size() - r[0]);
        res = min(res, (int)t.size() - l[n - 1]);
        return res;
    }
};

---