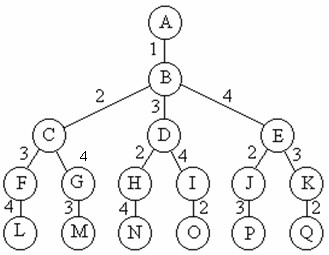
递归行为的时间复杂度估算

 整个递归过程是一棵多叉树，递归过程相当于利用栈做了一次后序遍历。

对于master公式，T(N)表明母问题的规模为N，T(N/b)表明每次子问题的规模，a为调用次数，加号后面表明，除去调用之外，剩余语句的复杂度是多少，算出d。根据上次三个判断公式进行算法时间复杂度计算。

归并排序（递归实现）

求出中点位置，先将左边部分排好序，再将右侧部分排好序，再整合（双指针），使得整体有序。

时间复杂度O(NlogN) ；空间复杂度O(N)

小和问题

看某个数右侧有多少数比该数大，那么就有这么多个该数对最后结果造成贡献（使用归并排序，在归并过程中进行计算）。和传统merge相比，在于左组数等于右组数时，在小和问题中一定要先拷贝右组的数。

 

逆序对问题 

同小和问题，只不过换成了判断左数组的数大于右数组的数。

315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）https://leetcode.cn/problems/count-of-smaller-numbers-after-self/
 

快速排序

问题一：准备一个变量，表示小于等于区域的右边界，如果当前数小于等于num，则把当前数和区域下一个数做交换，区域往右扩一个位置，当前数跳下一个。若当前数大于num，那么跳下一个数即可。

问题二：和问题一类似，两个区域，一个为小于区域的右边界i，一个为大于区域的左边界j，两个变量。当前数小于num，当前数和i数交换，i++，当前数跳下一个。当前数等于num，直接跳下一个。当前数大于num，当前数和j数交换，j--，当前数不动。

那么快速排序，就是以数组内最后一个数作为num，重复上述问题二，最后将大于区域第一个数与最后一个数交换，递归进行即可。

时间复杂度O(N^2)

但如果选取num是随机的，选出来与最后一个数交换然后做划分，可以避免出现最坏情况。

时间复杂度O(NlogN)