动态规划解决的问题

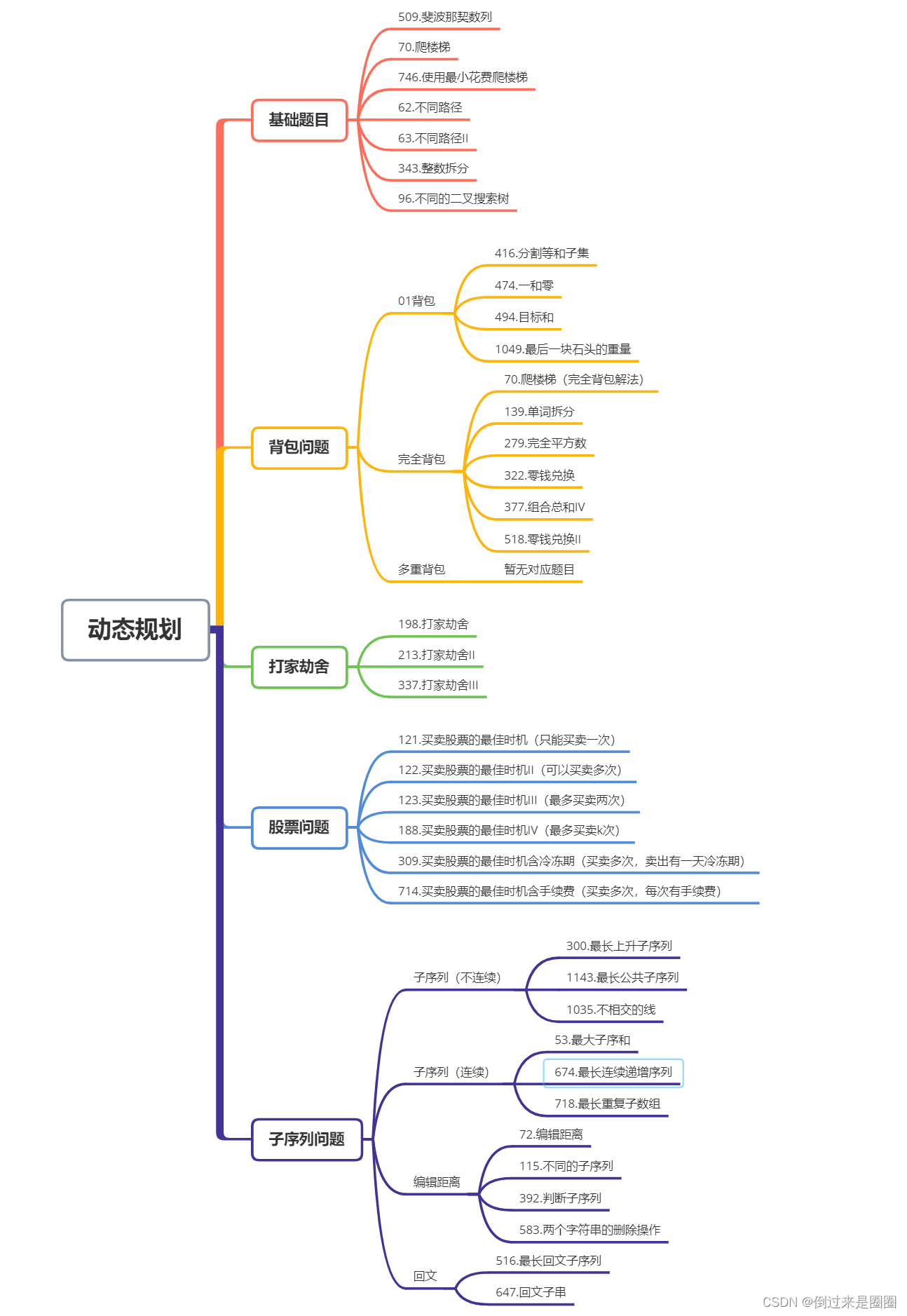
动态规划和贪心的区别：
动态规划是由前一个状态推导出来的；
贪心是局部直接选最优的。

动态规划解题步骤

1. 状态定义：确定dp数组以及下标的含义
2. 状态转移方程：确定递推公式
3. 初始条件：dp如何初始化
4. 遍历顺序
5. 举例推导dp数组

动态规划如何debug

把dp数组打印出来！！！看看究竟是不是按照自己的思路推导的！

做动规的题目，写代码前一定要把状态转移在dp数组上的具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。

然后再写代码，代码没通过->打印dp数组，看看是不是和自己预先推导的哪里不一样。

• 如果打印出来和自己预先模拟推导是一样的，那么就是自己的递归公式、初始化或者遍历顺序有问题了。
• 如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题。

如果代码写出来一直ac不了，灵魂三问：

1. 举例状态转移公式了吗？
2. 打印dp数组了吗？
3. 打印出来的dp数组和我想的一眼吗？

基础题目

1. 整数拆分

343. 整数拆分
给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

动态规划五部曲

1. 状态定义：dp[i] 表示分拆数字 i，可以得到的最大乘积。
2. 递推公式：假设对正整数 i 拆分出的第一个正整数是 j（1≤j<i），即 i 可以拆分成 i 和 i-j，则有以下两种情况
   （1）i-j不拆了：乘积为 j ∗ ( i − j )
   （2）i-j继续拆：乘积为 j ∗ dp [ i − j ]
   所以dp[i]=Math.max( j*(i-j) , j*dp[i-j] )
3. 初始条件：dp[0]=dp[1]=0，因为0和1无法拆分成两个正整数
4. 遍历顺序：观察递推公式，dp[i]依靠dp[i-j]，所以一定是从前往后遍历
5. 举例：n=10时，
   

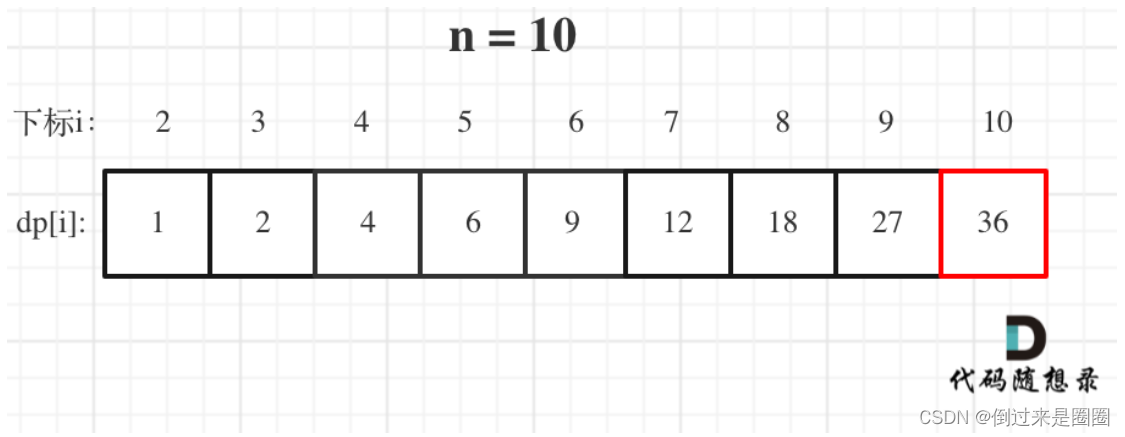
本题代码如下：

class Solution {
    public int integerBreak(int n) {
        int[] dp=new int[n+1];
        for(int i=2;i<=n;i++){
            for(int j=1;j<i;j++){
                dp[i]=Math.max(dp[i],Math.max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[n];
    }
}

时间复杂度：$O(n^2)$
空间复杂度：$O(n)$

2. 不同的二叉搜索树

96.不同的二叉搜索树
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

思路

给定一个有序序列 1⋯n，为了构建出一棵二叉搜索树，我们可以遍历每个数字 i，将该数字作为树根，将 1⋯(i−1) 序列作为左子树，将 (i+1)⋯n序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

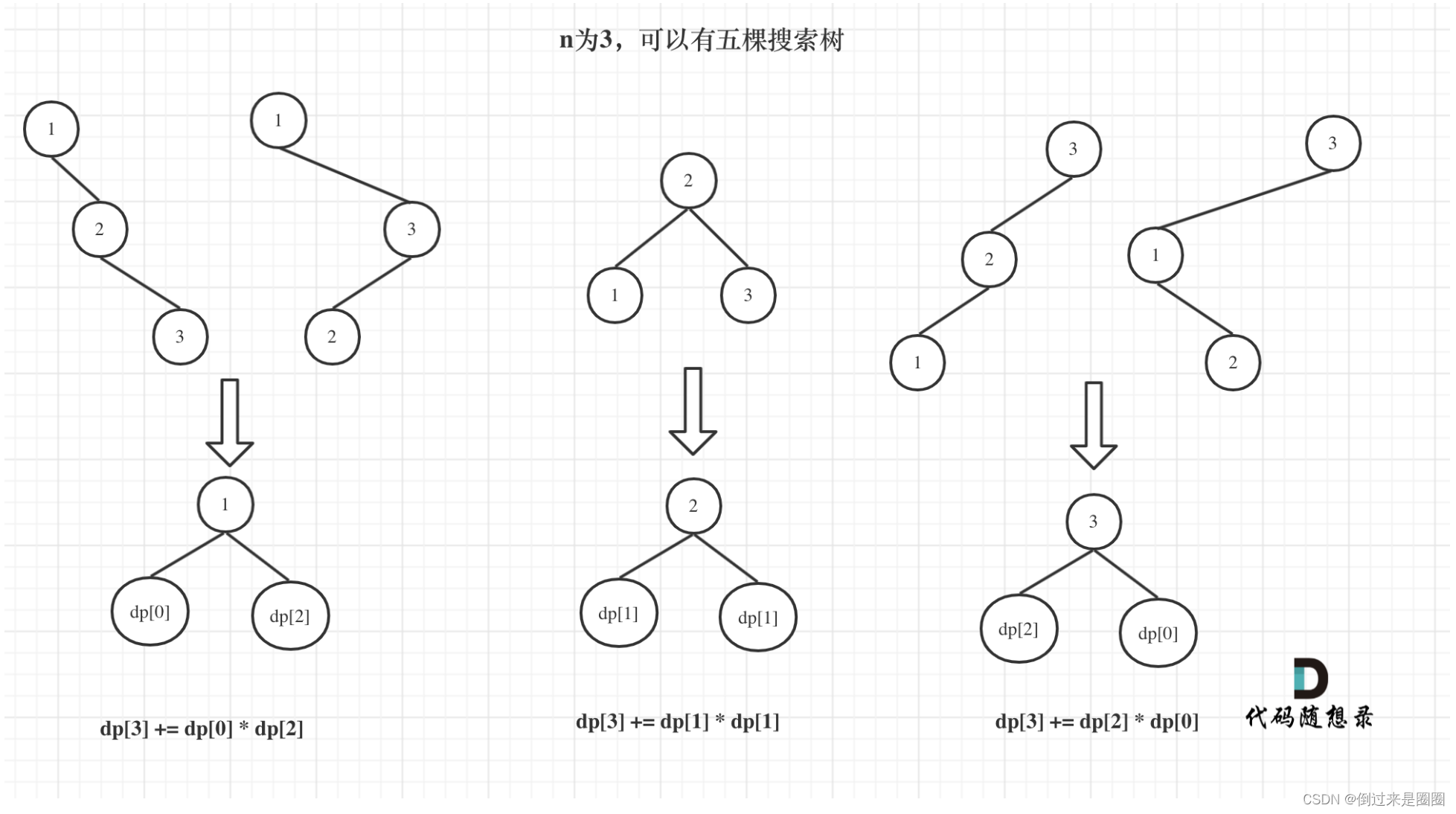
观察n=3时的五棵树：

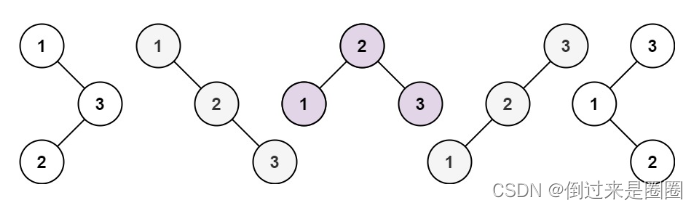
当1为树根时，右子树有两个节点，布局和n=2时两棵树的布局一致；
当3为树根时，左子树有两个节点，布局也和n=2时两棵树的布局一致；
当2为树根时，其左右子树都只有一个节点，布局和n=1时一棵树的布局一致。

所以dp[3]=元素1为根的搜索树数量dp[1]+元素2为根的搜索树数量dp[2]+元素3为根的搜索树数量dp[3]，
而dp[1]=右子树有2个元素的搜索树数量$\ast$左子树有0个元素的搜索树数量，
dp[2]=右子树有1个元素的搜索树数量$\ast$左子树有1个元素的搜索树数量，
dp[3]=右子树有0个元素的搜索树数量$\ast$左子树有2个元素的搜索树，
即dp[3]=dp[2]*dp[0]+dp[1]*dp[1]+dp[0]*dp[2]。

如图所示，

动态规划五部曲

1. 状态定义：dp[i] 表示1~i 节点组成的二叉搜索树的个数。
2. 递推公式：由思路中看出，dp[i]+=dp[以 j 为根左子树节点数量]*dp[以 j 为根右子树节点数量]，j 从1到 i
   所以dp[i]+=dp[j-1] * dp[i-j]。
   （j-1作为左子树，i-j作为右子树是由二叉搜索树的定义决定的）
3. 初始条件：dp[0]=1，因为从定义上来说，空节点也是一棵二叉搜索树。
4. 遍历顺序：观察递推公式，dp[i]依靠dp[j-1]和dp[i-j]，所以一定是从前往后遍历。
5. 举例：n=5时，
   

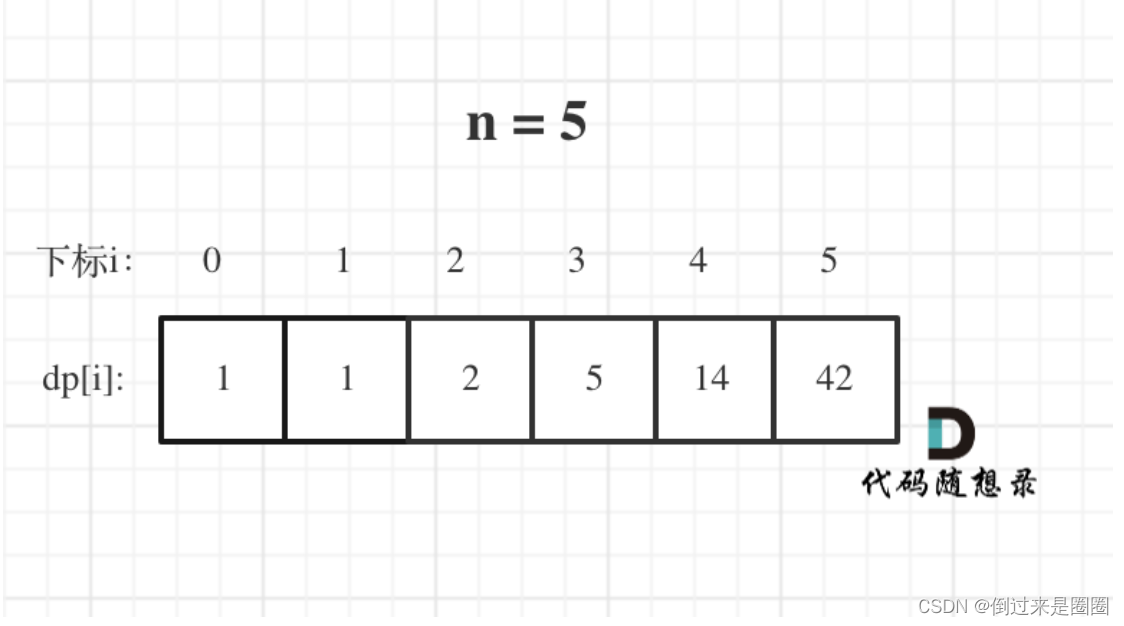
本题代码如下：

class Solution {
    public int numTrees(int n) {
        int[] dp=new int[n+1];
        dp[0]=1;//空节点也是一棵二叉搜索树
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i]+=dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
}

时间复杂度：$O(n^2)$
空间复杂度：$O(n)$

01背包问题

理论基础

区分01背包、完全背包和多重背包：

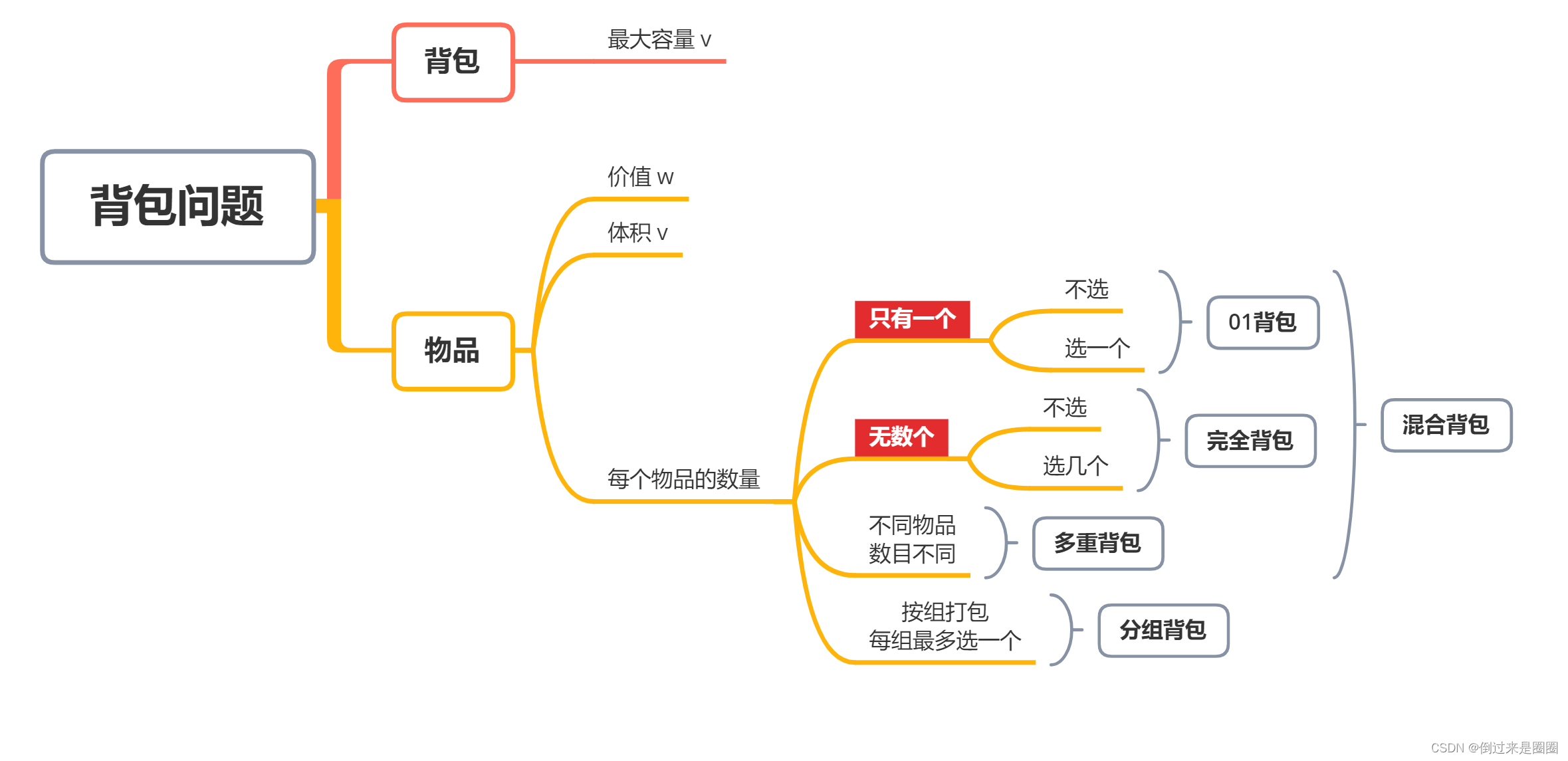
重中之重是01背包，多重背包力扣上甚至没有相应的题目。

01背包

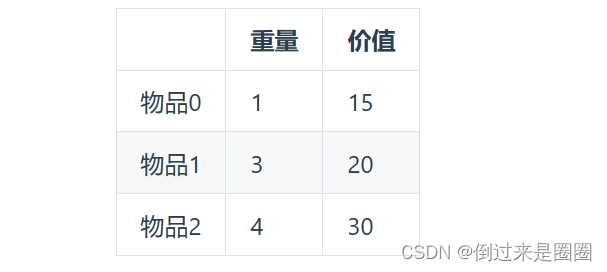
有n件物品和一个最多能背重量为 w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

二维dp数组-01背包

1. 状态定义：dp[i][j] 表示从下标为[0-i]的物品里任意取，重量是 j 时背包内最大价值总和。
   

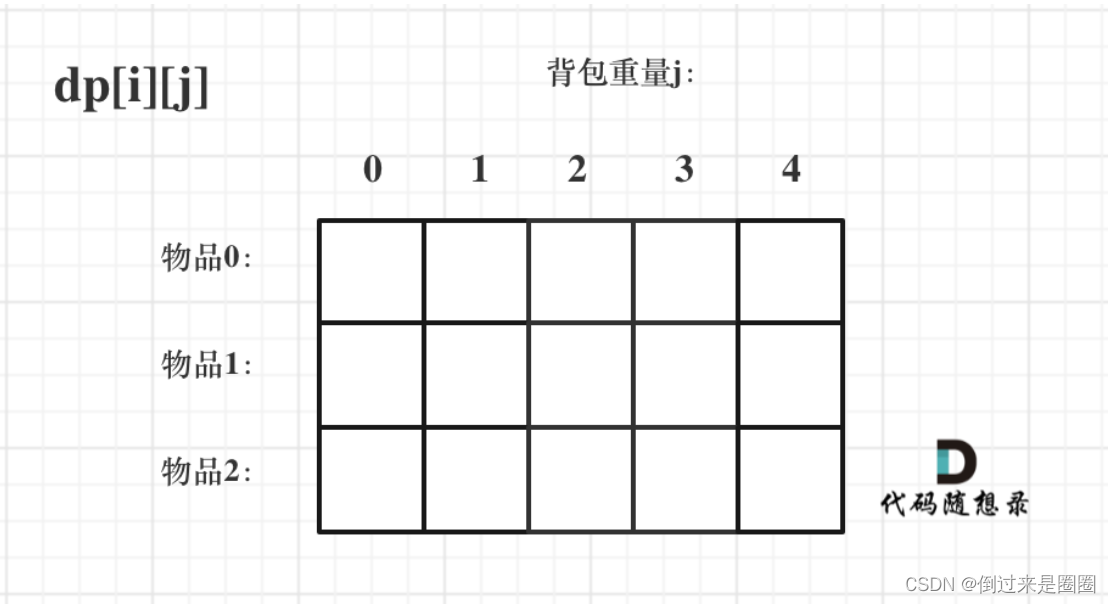
2. 递推公式：
   （1）不放物品 i ：dp[i][j]=dp[i-1][j]，不放物品i，背包价值依然和前面相同；
   （2）放物品 i ：dp[i][j]=dp[i-1][ j-weight[i] ]+value[i]，背包容量为j - weight[i]时，不放物品i的最大价值为dp[i - 1][j - weight[i]] ，所以放入物品i以后价值增加value[i]；
   所以dp[i][j]=max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])。

3. 初始条件：观察递推公式，dp[0][j]是一定要初始化的，否则后面的状态无法推出，
   （1）背包容量j=0：无论取哪些物品，背包价值总和一定为0，因此dp[i][0]=0；
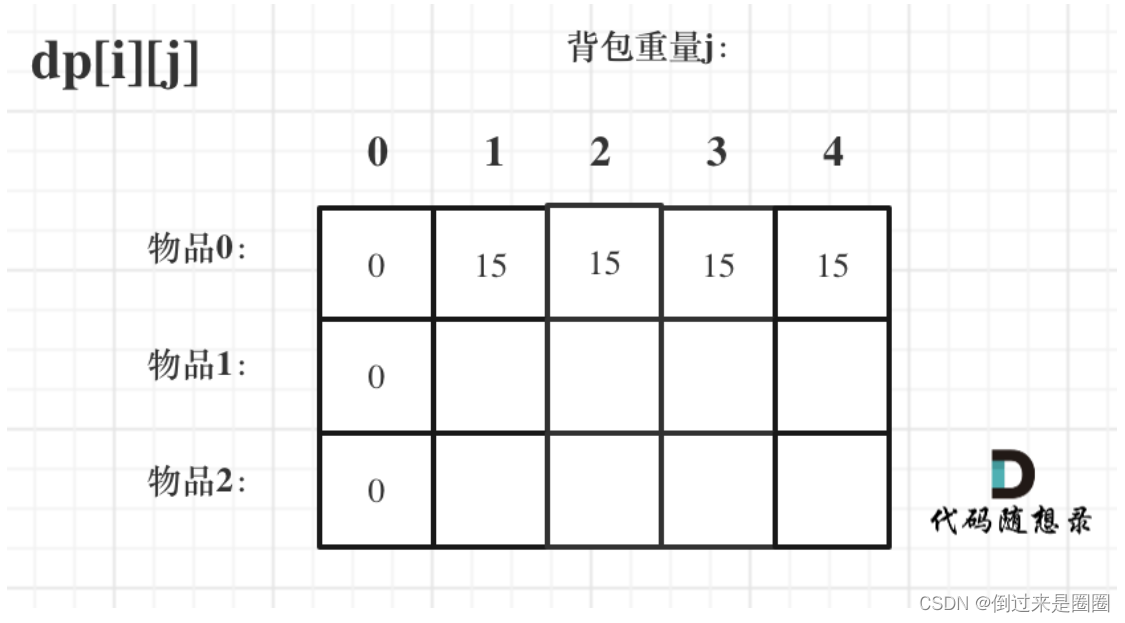
   （2）物品最大下标i=0：只能取0号物品，
   如果 j<weight[i]，背包装不下0号物品，价值为0；
   如果 j>=weight[i]，背包只能装0号物品，价值等于0号物品的价值；
   

4. 遍历顺序：先遍历物品再遍历背包，或者先遍历背包再遍历物品都可以。
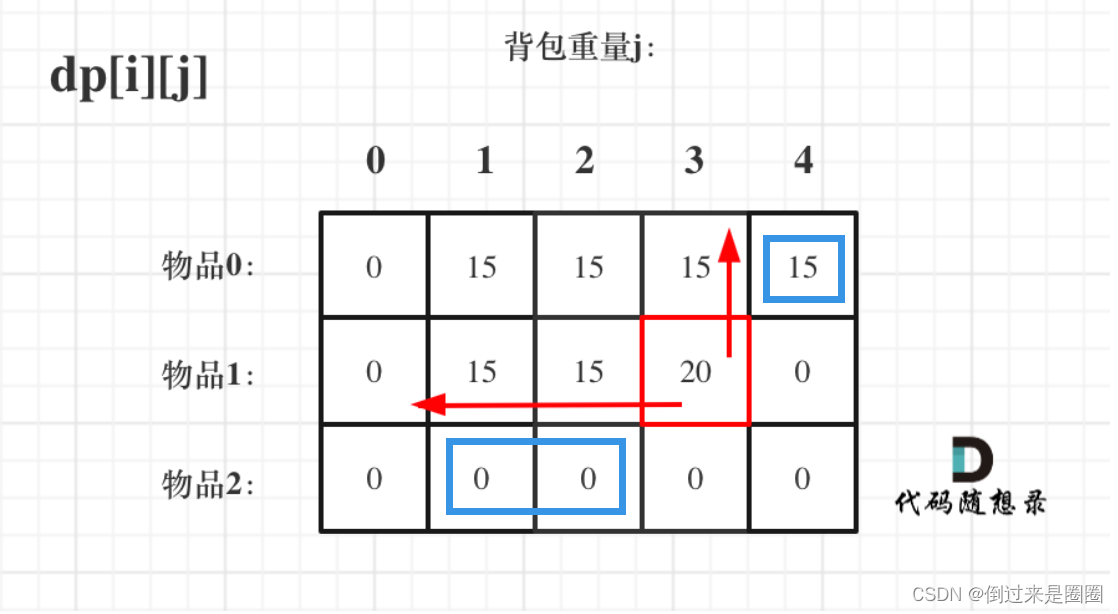
   根据递推公式，dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括正上方向），那么先遍历物品再遍历背包过程如下所示：
   

for(int i=1;i<weight.length;i++){//遍历物品
   for(int j=0;j<=bagweight;j++){//遍历背包重量
        if(j<weight[i])
            dp[i][j]=dp[i-1][j];
        else
            dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]+value[i]]);
    }
}

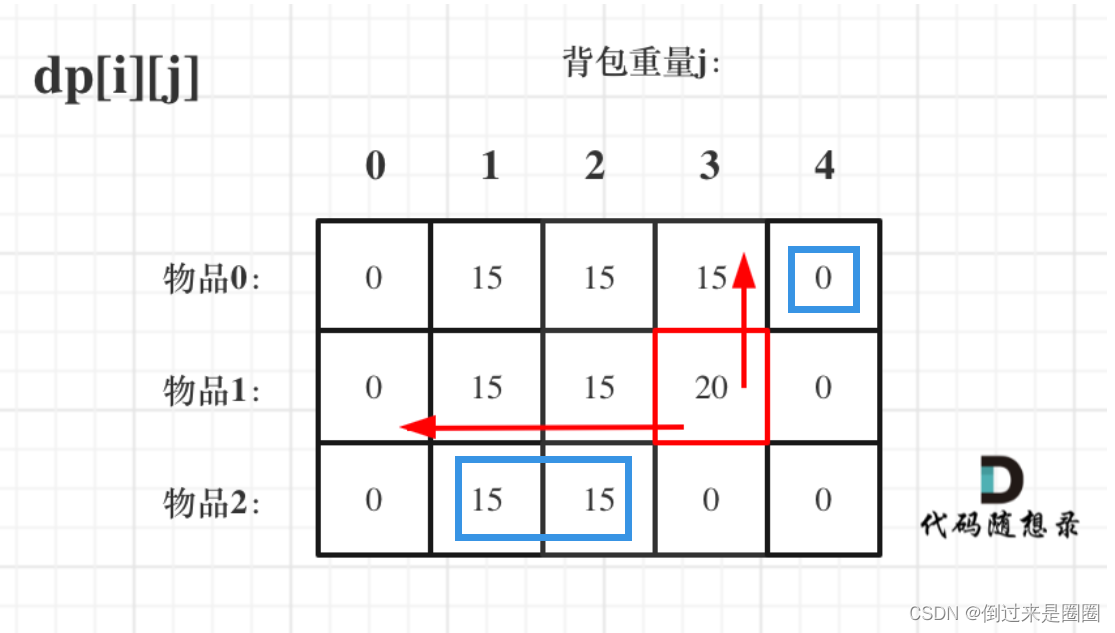
而先遍历背包再遍历物品的过程如下所示：

for(int j=0;j<=bagweight;j++){//遍历背包重量
    for(int i=1;i<weight.length;i++){//遍历物品
        if(j<weight[i])
            dp[i][j]=dp[i-1][j];
        else
            dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]+value[i]]);
    }
}

不管哪种方式，更新dp[i][j]需要的就是左上角，两种方式均不影响dp[i][j]的推导。

5. 举例：背包最大重量为4，
   
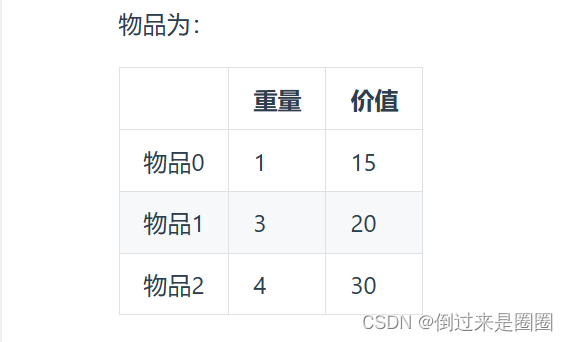
   则推出dp的数值如下，
   
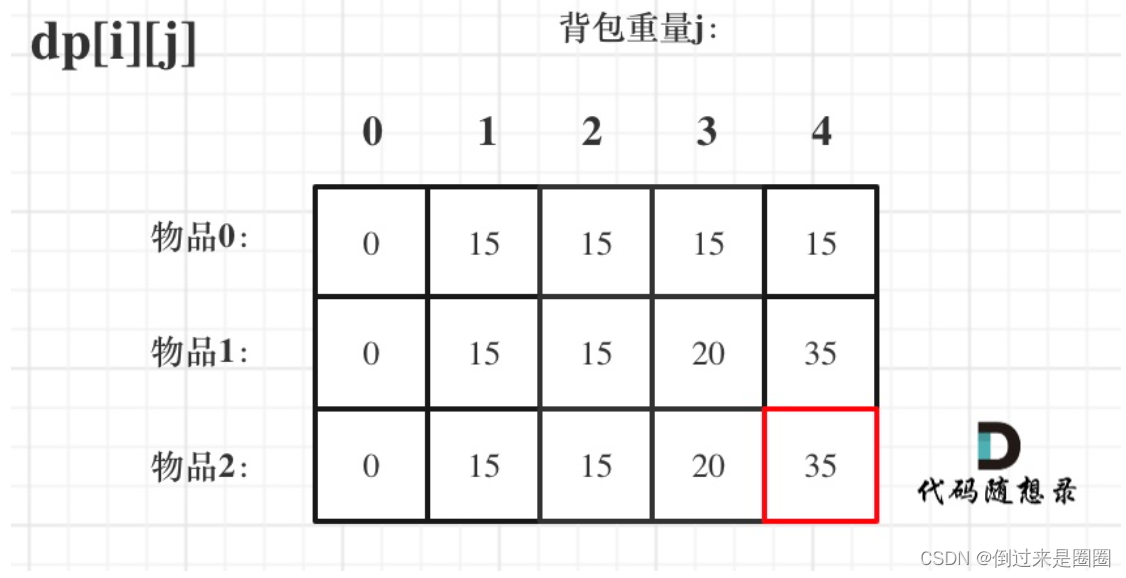
   最终结果就是dp[2][4]。

一维dp数组-01背包

观察上述递推公式，dp[i][j]=max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])，发现第 i 行的状态只与第 i-1 行的状态有关，所以可以用滚动数组优化01背包的空间。

1. 状态定义：dp[j] 表示容量为 j 的背包所背的最大价值。
2. 递推公式：dp[j]=max(dp[j], dp[j-weight[i]] + value[i])
3. 初始条件：dp[0]=0，背包装不了东西的时候价值自然是0.
4. 遍历顺序：
   注意这里背包重量一定是倒序遍历，否则当前状态会与之前取得状态重合！
   除此之外，**两个for循环的顺序也不能颠倒！**因为根据一维dp的写法，背包容量一定是要倒序遍历的，而如果容量放在上一层，那么每个dp[j]就只会放入一个物品，即背包里只放入了一个物品。

for(int i=0;i<weight.length;i++){//遍历物品
    for(int j=bagweight;j>=weight[i];j--){//遍历背包重量(反向)
        dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]+value[i]]);
    }
}

5. 举例：背包最大重量为4，
   
   

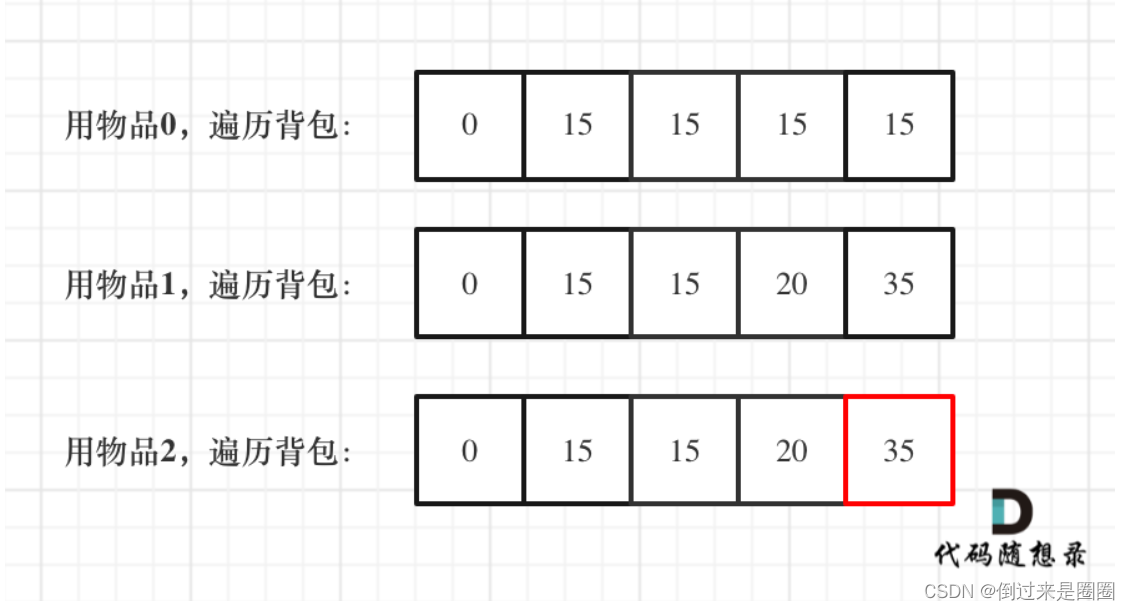
完整代码如下：

class Solution {
    public boolean bagpack(int[] nums) {
        int[] dp=new int[bagweight+1];
        for(int i=0;i<weight.length;i++){//遍历物品
            for(int j=bagweight;j>=weight[i];j--){//遍历背包重量(反向)
                dp[j]=Math.max(dp[j],dp[j-weight[i]+value[i]]);
            }
        }
        return dp[bagweight];
    }
}

一维数组的01背包代码更加简洁，空间复杂度还比二维dp数组下降了一个数量级。

quiz

对于纯二维01背包，先实现，然后提问：

• 为什么两个for循环的嵌套这么写？反过来写行不行？为什么？

对于一维数组的01背包，实现，然后提问：

• 两个for循环的顺序反过来写行不行？为什么？

1. 分割等和子集

416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

思路

首先，本题要求集合中能否出现总和为sum/2的子集；其次，数组中元素只能用一次，不可重复使用，因此考虑01背包而不是完全背包；接着，将题目中给定条件与01背包一一对应。

• 背包体积为sum/2
• 背包物品->集合元素，物品重量->元素数值，物品价值->元素数值
• 背包正好装满，说明找到了总和为sum/2的子集
• 每一个元素不可重复放入

动态规划五部曲

1. 状态定义：dp[j] 表示背包容量是 j 时，所背的最大重量。
   本题每一个元素的数值既是重量，也是价值。当dp[target]==target时，说明背包装满了。
   那什么时候装不满呢？以[1,5,11,5]举例，dp[7]只能等于6，即装不满；而dp[6]就可以等于6，则说明装满了。
2. 递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])，同01背包。
3. 初始条件：dp[0]=0，背包重量为0时，说明没装东西，价值必然是0。
4. 遍历顺序：同01背包问题，

for(int i=0;i<n;i++){
    for(int j=target;j>=nums[i];j--){
        dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
    }
}

5. 举例：
   dp[j]的值一定是小于等于 j 的。
   如果dp[j]==j，说明集合中的子集总和正好可以凑成总和 j 。
   以输入[1,5,11,5] 为例，如图，
   
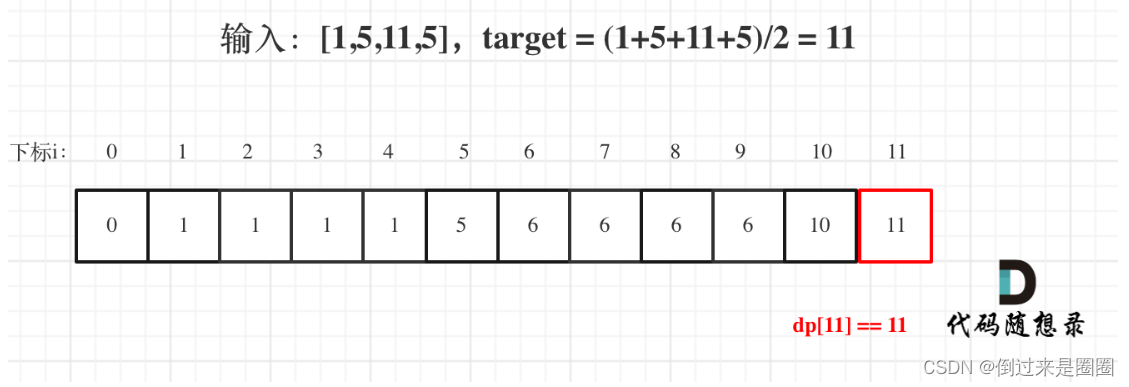
   最后dp[11]==11，说明可以将这个数组分割成两个子集，使得两个子集的元素和相等。

完整代码如下：

class Solution {
    public boolean canPartition(int[] nums) {
        int n=nums.length,sum=0;
        for(int num:nums)
            sum+=num;
        if(n<2||sum%2==1)
            return false;
        int target=sum/2;
        int[] dp=new int[target+1];
        for(int i=0;i<n;i++){
            for(int j=target;j>=nums[i];j--){
                dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        return dp[target]==target?true:false;
    }
}

时间复杂度：$O(n^2)$
空间复杂度：$O(n)$

2. 最后一块石头的重量 II

1049. 最后一块石头的重量 II【中等】
有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为
  y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

思路

本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，和前一道416. 分割等和子集非常像，化解为01背包问题。

石头的重量stones[i]对应01背包中物品的重量weight[i]和物品价值value[i]。

动态规划五部曲

1. 状态定义：dp[j] 表示背包容量是 j 时，所背的最大重量。
2. 递推公式：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])，同01背包。
3. 初始条件：dp[i]=0，背包重量为0时，说明没装东西，价值必然是0。
4. 遍历顺序：同01背包问题，

for(int i=0;i<n;i++){
    for(int j=target;j>=stones[i];j--){
        dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
    }
}

5. 举例：输入[2,4,1,1]，此时target=(2+4+1+1)/2=4，dp数组如图，
   
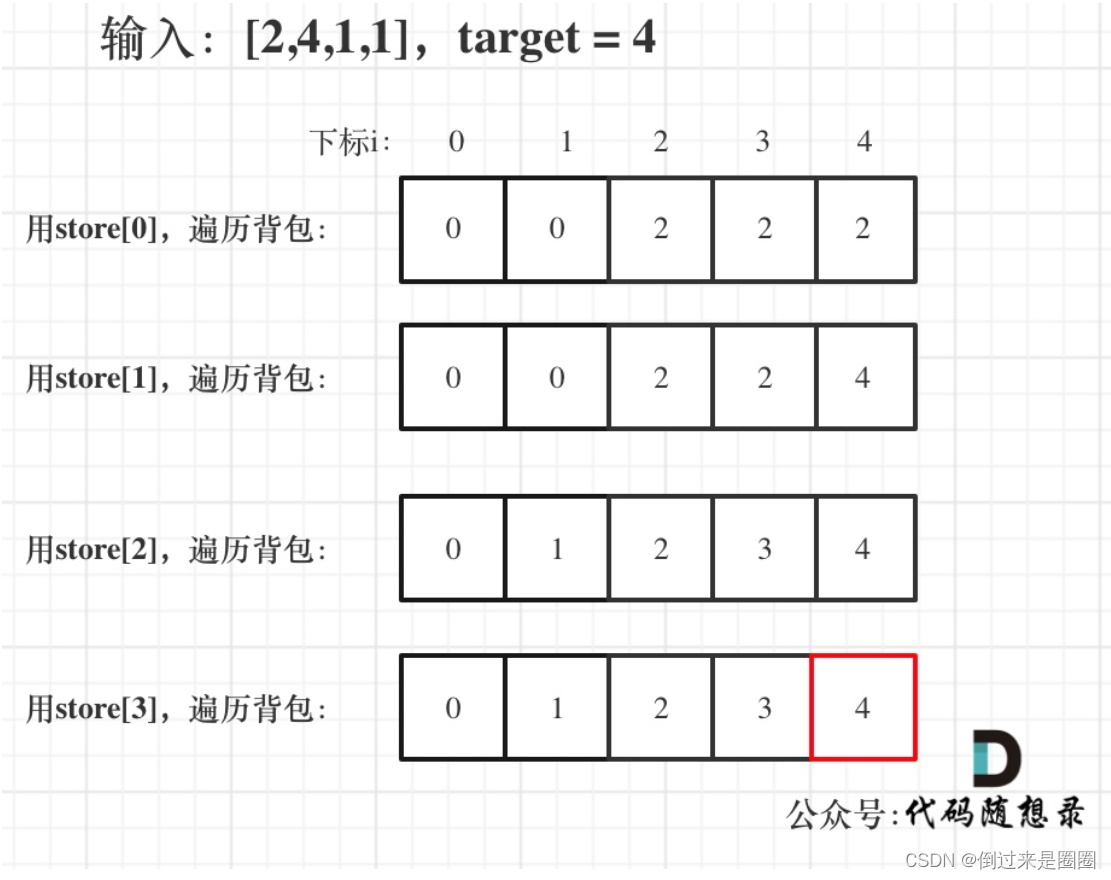
   最后 dp[target] 中是容量为target的背包能背的最大重量。
   那么分成两堆石头，一堆石头总重量为 dp[target] ，另一堆石头重量则为 sum-dp[target]。
   在计算target时，sum/2是向下取整，所以sum-dp[target]一定大于等于dp[target]。
   那么相撞以后剩下的最小石头重量就是(sum-dp[target])-dp[target]。

完整代码如下：

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int n=stones.length,sum=0;
        for(int w:stones){
            sum+=w;
        }
        int target=sum/2;
        int[] dp=new int[target+1];
        for(int i=0;i<n;i++){
            for(int j=target;j>=stones[i];j--){
                dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        return sum-2*dp[target];
    }
}

时间复杂度：O(m × n) , m是石头总重量（准确的说是总重量的一半），n为石头块数
空间复杂度：O(m)

3. 目标和

494. 目标和
给你一个整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

思路

本题要如何使表达式结果为target。
想到一定有 left组合-right组合=target，而 left+right=sum，sum固定，所以right=sum-left，代入。
得到公式left-(sum-left)=target，即left=(sum+target)/2。
sum和target是固定的，因此问题转化为在集合nums中找到满足条件的left组合。

动态规划五部曲

经过上述分析，本题可以转化为，装满容量为x的背包，有多少种方法。

由于x=(sum+target)/2，那么当sum+target为奇数时，问题无解。例如sum=5，target=2时，直接返回0。
同时，如果abs(target)>sum，问题也是无解的。注意一定要加绝对值，因为如果target是负数，虽然target可能小于sum，但是abs(target)>sum，所以即使全用负号，也无法到达目标和。

由于每个数组元素只能取一次，所以将问题转化为01背包问题。

之前的01背包问题都是求容量为 j 的背包，最多能装多少。
本题则是装满有几种方法，转化为一个组合问题。

1. 状态定义：dp[j] 表示装满背包容量 j ，有多少种方法（不同于之前的最大价值）。
2. 递推公式：
   只要搞到nums[i]，凑成dp[j]就有dp[j-nums[i]]种方法。
   举个例子，求背包重量为5时的方法数dp[5]，
   （1）已经有一个1（nums[i]）的话，有dp[4]种方法凑成重量为5的背包。
   （2）已经有一个2（nums[i]）的话，有dp[3]种方法凑成重量为5的背包。
   （3）已经有一个3（nums[i]）的话，有dp[2]种方法凑成重量为5的背包。
   （4）已经有一个4（nums[i]）的话，有dp[1]种方法凑成重量为5的背包。
   （5）已经有一个5（nums[i]）的话，有dp[0]种方法凑成重量为5的背包。
   那么凑成dp[5]有多少种方法呢？也就是把所有的dp[j-nums[i]]累加起来。
    
   因此递推公式：dp[j] += dp[j - nums[i]] 。
   （在求装满背包有几种方法的情况下，递推公式一般都是上面这个！
3. 初始条件：dp[0]=1，背包重量为0时，只有啥也不装一种方法。
4. 遍历顺序：顺序同01背包问题，仅递推公式改变，

for(int i=0;i<n;i++){
    for(int j=bagSize;j>=nums[i];j--){
        dp[j]+=dp[j-nums[i]];
    }
}

5. 举例：输入[1,1,1,1,1]，target=3，则bagSize=(5+3)/2=4，dp数组如下，
   

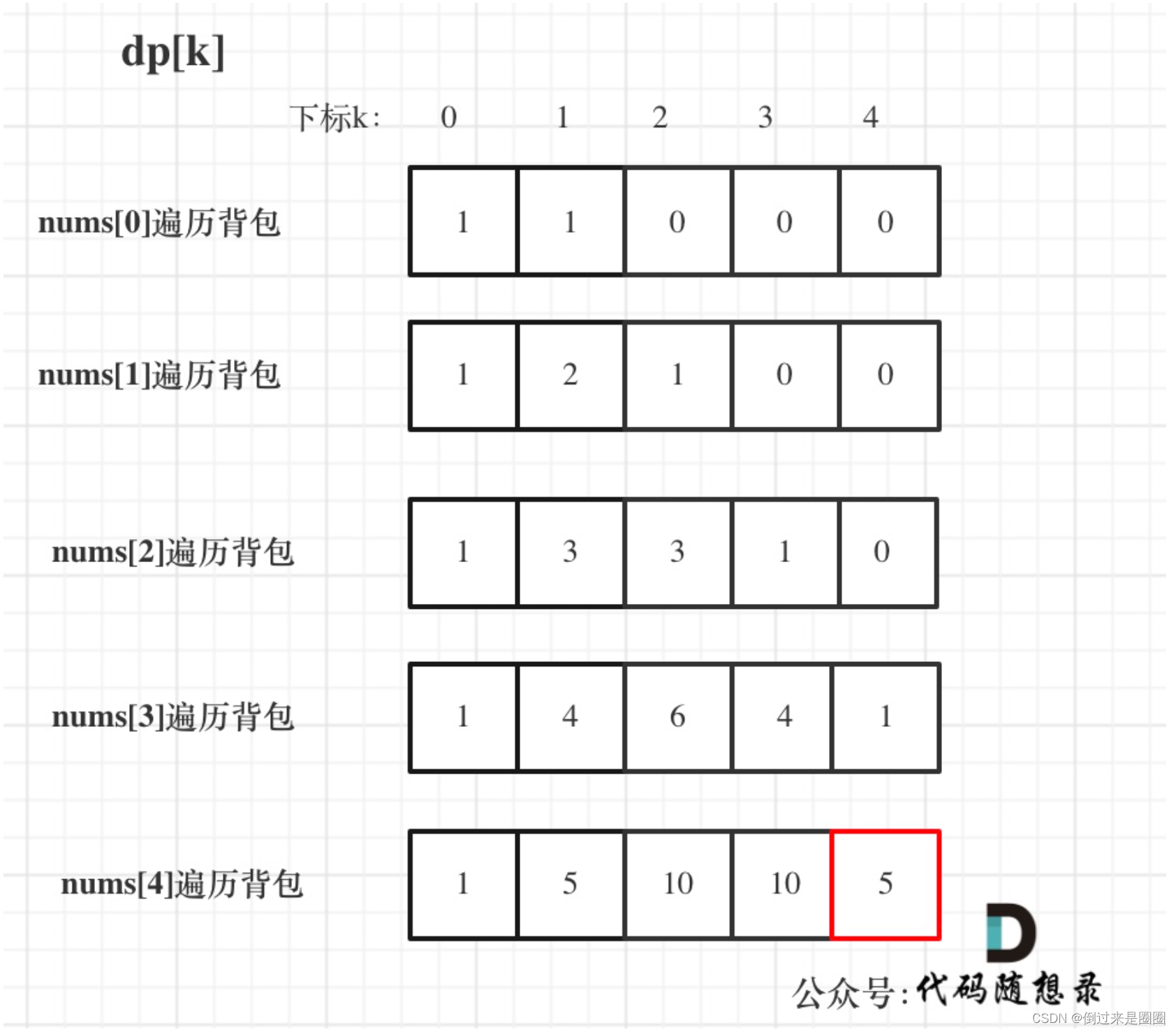
完整代码如下：

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int n=nums.length,sum=0,res=0;
        for(int num:nums)
            sum+=num;
        if(Math.abs(target)>sum||(sum+target)%2==1)
            return 0;
        int bagSize=(sum+target)/2;
        int[] dp=new int[bagSize+1];
        dp[0]=1;
        for(int i=0;i<n;i++){
            for(int j=bagSize;j>=nums[i];j--){
                dp[j]+=dp[j-nums[i]];
            }
        }
        return dp[bagSize];
    }
}

时间复杂度：O(n × m)，n为正数个数，m为背包容量
空间复杂度：O(m)，m为背包容量

4. 一和零

474.一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

思路

本题strs数组里的元素就是物品，每个物品都是一个！
而m和n相当于是一个背包，两个维度的背包。
将本题转化为01背包问题，背包有两个维度，一个m维度一个n维度，而不同长度的字符串就是不同大小的代装物品。

动态规划五部曲

1. 状态定义：dp[i][j] 表示最多有 i 个0和 j 个1的最大strs子集大小。
2. 递推公式：设strs里的字符串有zeroNum个0，oneNum个1，
   dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1)
   对比标准01背包的递推公式，发现字符串的zeroNum和oneNum相当于物品的重量weight[i]，字符串本身的个数相当物品的价值value[i]。
   所以这就是一个典型的01背包问题，只不过物品的重量有了两个维度。
3. 初始条件：dp[0][0]=0。
4. 遍历顺序：同01背包问题，外层遍历物品，内层反向遍历背包容量，

for(String str:strs){//遍历物品
    //统计字符串中0和1的数量
    int zeroNum=0,oneNum=0;
    for(int k=0;k<str.length();k++){
        char ch=str.charAt(k);
        if(ch=='0') zeroNum++;
        else    oneNum++;
    }
    //遍历背包容量（两个维度）
    for(int i=m;i>=zeroNum;i--){
        for(int j=n;j>=oneNum;j--){
            dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);
        }
    }
}

5. 举例：输入[“10”,“0001”,“111001”,“1”,“0”]，m = 3，n = 3，最后的dp数组状态如图，
   

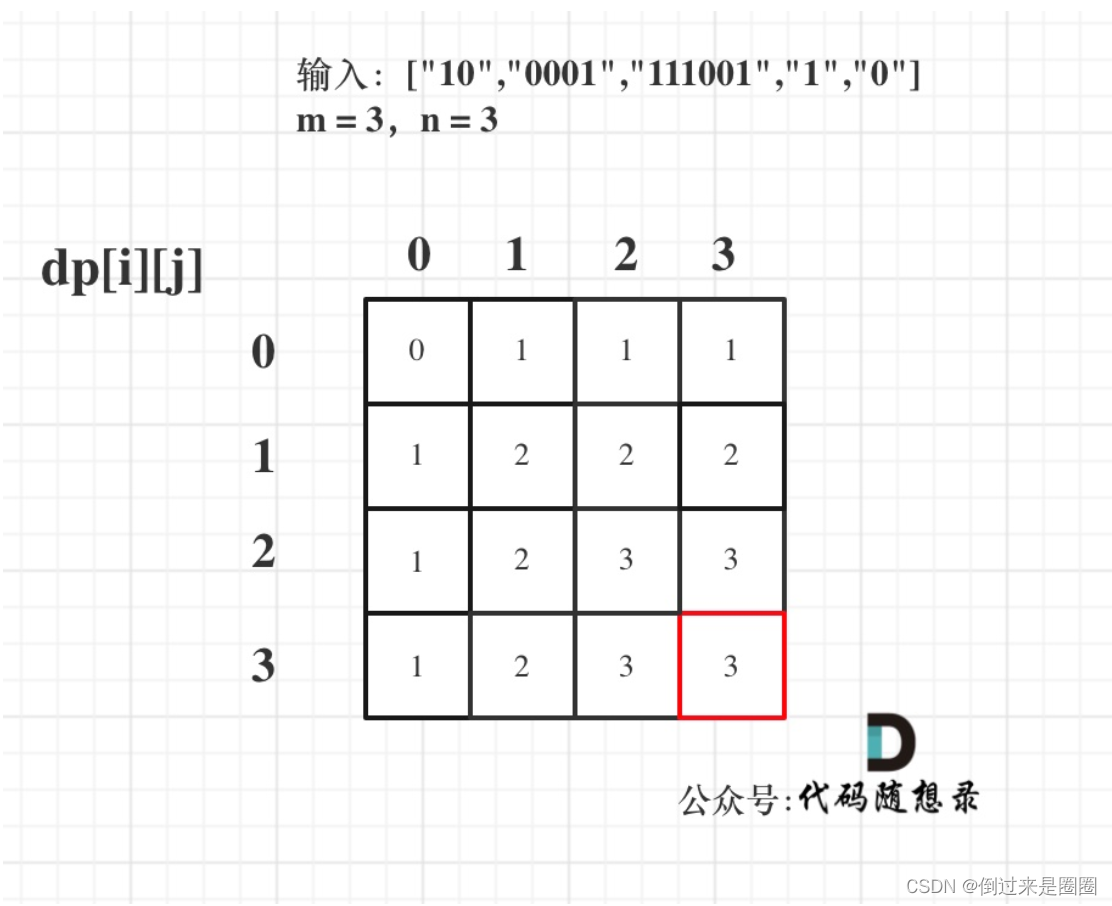
完整代码如下：

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][] dp=new int[m+1][n+1];
        for(String str:strs){
            //统计字符串中0和1的数量
            int zeroNum=0,oneNum=0;
            for(int k=0;k<str.length();k++){
                char ch=str.charAt(k);
                if(ch=='0') zeroNum++;
                else    oneNum++;
            }
            //计算dp
            for(int i=m;i>=zeroNum;i--){
                for(int j=n;j>=oneNum;j--){
                    dp[i][j]=Math.max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);
                }
            }
        }
        return dp[m][n];
    }
}

完全背包问题

理论基础

问题描述：有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

同样举01背包中的例子，背包最大重量为4，物品为：

每件商品都有无限个！
问背包能背的物品最大价值是多少？

完全背包和01背包唯一不同就是体现在遍历顺序上！ 所以下面对遍历顺序进行分析。

01背包核心代码：

/*01背包核心代码*/
for(int i=0;i<weight.length;i++){//遍历物品
    for(int j=bagweight;j>=weight[i];j--){//遍历背包重量(反向)
        dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]+value[i]]);
    }
}

其中内循环从大到小反向遍历，为了保证每个物品仅被添加一次。

而完全背包物品可以添加多次，所以要从小到大正向遍历，即：

/*完全背包核心代码*/
for(int i=0;i<weight.length;i++){//遍历物品
    for(int j=weight[i];j<=bagweight;j++){//遍历背包重量(正向)
        dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]+value[i]]);
    }
}

对于上例，dp状态图如下：

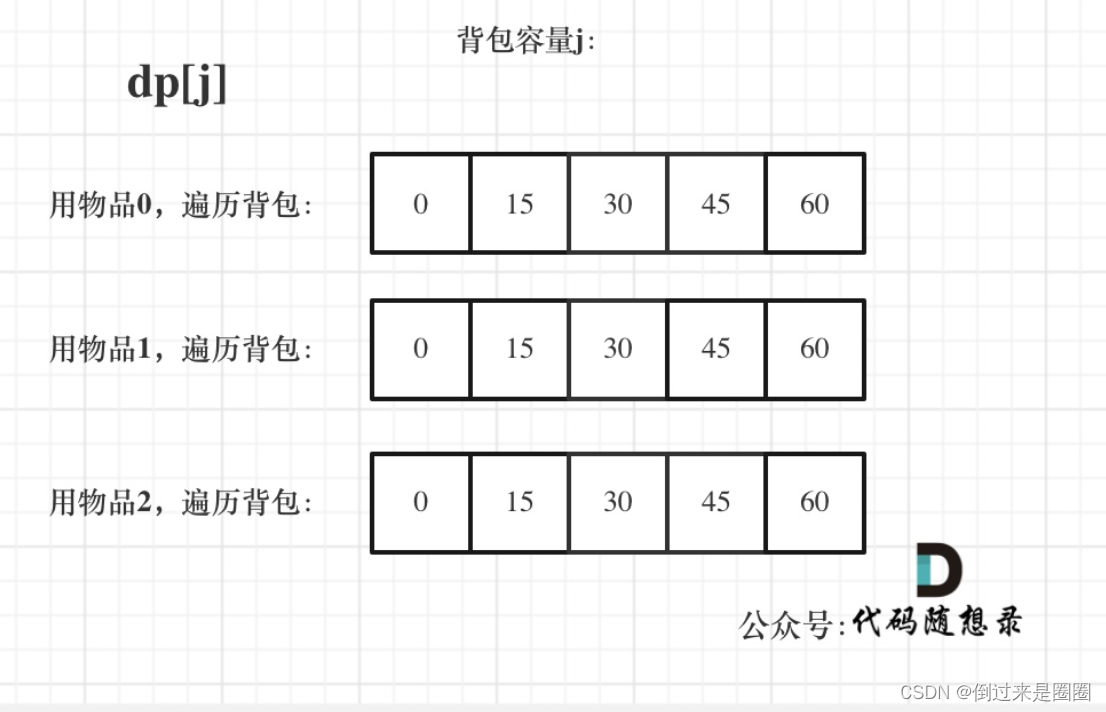
除此之外，需要注意的一点是，不同于01背包，一维dp的完全背包两层for循环的顺序是可以颠倒的！ 因为只要保证下标 j 之前的dp[j]都是计算过的就可以了。

先背包容量(j)再遍历物品(i) 的代码如下：

// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j-weight[i] >= 0) 
        	dp[j] = max(dp[j],dp[j-weight[i]]+value[i]);
    }
}

注意：对于纯完全背包问题，for循环的先后顺序无所谓；但是如果题目稍有变化，比如问装满背包有几种方式的话，for循环的先后顺就有很大区别了，注意分析！

排列数 v.s 组合数

对比下面两题，

518. 零钱兑换 II
给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。 假设每一种面额的硬币有无限个。

377. 组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
 
请注意，顺序不同的序列被视作不同的组合。

零钱兑换II 中求可以凑成amount的硬币组合数，
组合总和IV 中同样求凑成target的元素组合个数，但不同顺序的序列被视作不同组合，即实际上求的是元素的排列数！

实现起来，两者的在于for循环的遍历顺序！

• 求组合数：外层for遍历物品（i），内层for遍历背包（j）。
• 求排列数：外层for遍历背包（j），内层for遍历物品（i）。

对比一下两题的dp数组状态：
零钱兑换II：每一个coin只进入计算一次【组合】

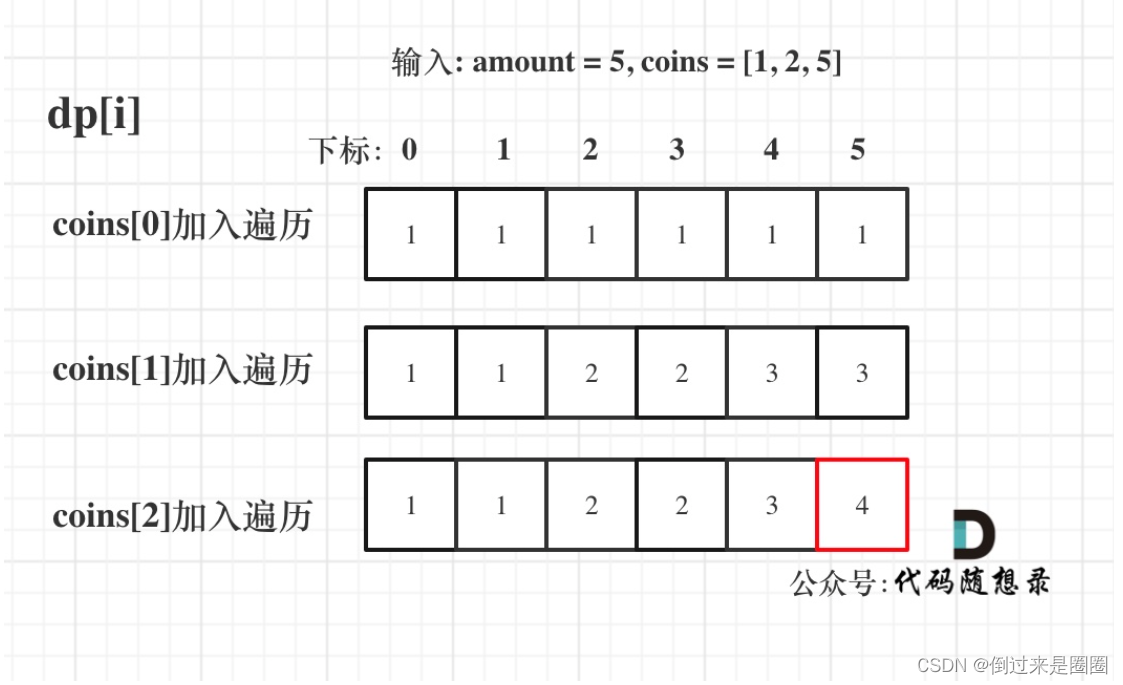
组合总和IV：背包的每一个值，都经过了所有num的计算【排列】

1. 零钱兑换

322. 零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

动态规划五部曲

1. 状态定义：dp[j] 表示凑足总额为j所需钱币的最少个数。
2. 递推公式：凑足总额为j - coins[i]的最少个数为dp[j - coins[i]]，那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j]（考虑coins[i]）
   所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
   dp[j] = min(dp[j], dp[j-coins[i]] + 1)。
3. 初始条件：考虑递推公式的特性，dp[j]必须初始化为一个最大的数，否则就会在min(dp[j], dp[j-coins[i]] + 1)被初始值覆盖
   所以令dp[0]=0，其余dp[j]=amount+1。
4. 遍历顺序：本题求钱币最小个数，那么钱币有顺序和没有顺序都可以，都不影响钱币的最小个数。
   所以本题并不强调集合是组合还是排列。
   由于本题钱币数量无限使用，因此属于完全背包问题，遍历内循环一定是正序，但两个for循环先后顺序无所谓。

for(int i=0;i<n;i++){
    for(int j=0;j<=amount;j++){
        dp[j]=Math.min(dp[j], dp[j-coins[i]] + 1);
    }
}

5. 举例：以输入：coins = [1, 2, 5], amount = 5为例，dp数组状态如下，
   

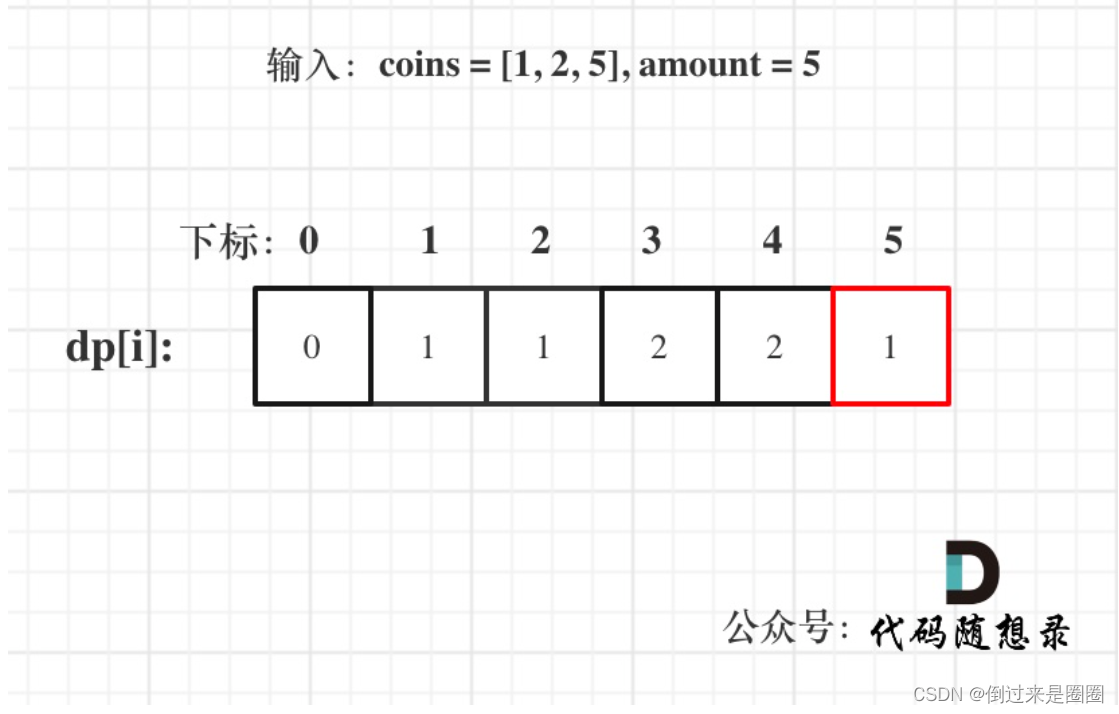
完整代码如下：

class Solution {
    public int coinChange(int[] coins, int amount) {
        int n=coins.length;
        int[] dp=new int[amount+1];
        Arrays.fill(dp,amount+1);
        dp[0]=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<=amount;j++)
                if(j>=coins[i])
                    dp[j]=Math.min(dp[j],dp[j-coins[i]]+1);
        }
        return dp[amount]==amount+1?-1:dp[amount];
    }
}

2. 单词拆分

139. 单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

动态规划五部曲

本题中单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。
由于字典中单词可以重复使用，因此属于一个完全背包问题。

1. 状态定义：dp[i] 表示字符串长度为 i 时，是否可以拆分为一个或多个在字典中出现的单词。
2. 递推公式：如果dp[j]==true，且 s[j,i] 子串出现在字典里，那么dp[i]一定是true。（j<i）
   if([j,i] 这个区间的子串出现在字典里&& dp[j]==true)
dp[i] = true;
3. 初始条件：dp[0]=true，
   考虑递推公式的特性，dp[i]必须依赖于dp[j]，dp[0]是一切的根基，因此必须要为true，否则就递推不下去了。
4. 遍历顺序：单词的顺序改变字符串改变，所以本题属于排列问题
   外层for循环遍历背包容量（字符串），内层for循环遍历物品重量（单词）。

求组合数：动态规划：518.零钱兑换II
求排列数：动态规划：377. 组合总和 Ⅳ、动态规划：70.爬楼梯进阶版（完全背包）
求最小数：动态规划：322. 零钱兑换、动态规划：279.完全平方数

5. 举例：以输入: s = “leetcode”, wordDict = [“leet”, “code”]为例，dp状态如图，
   

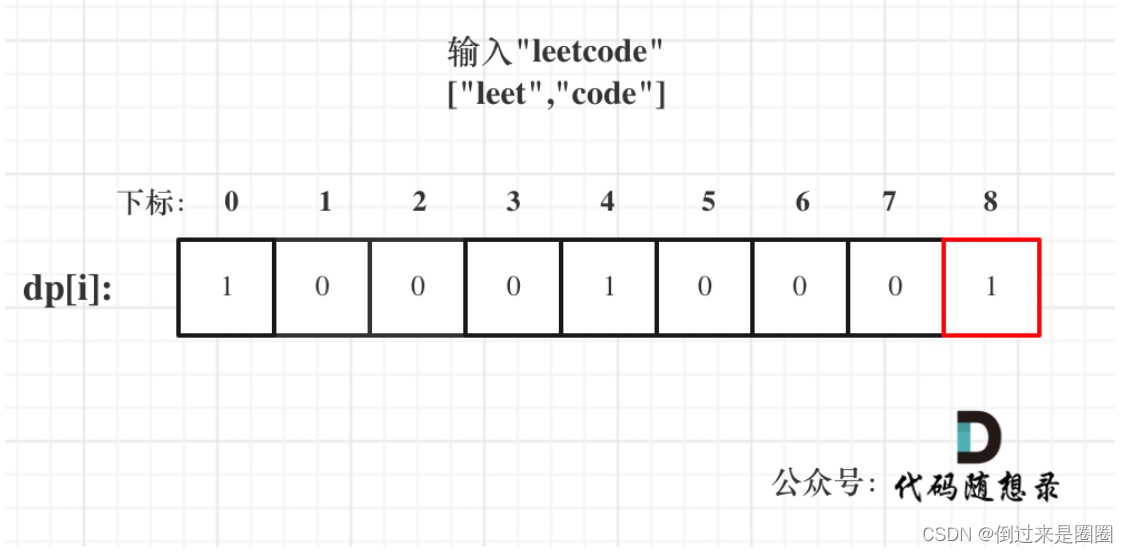
完整代码如下：

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n=s.length(),m=wordDict.size();
        Set<String>words=new HashSet<>(wordDict);
        boolean[] dp=new boolean[n+1];
        dp[0]=true;
        for(int i=1;i<=n;i++){
            for(int j=0;j<i;j++){
                String word=s.substring(j,i);
                //字典中查找s[j,i]
                if(dp[j]&&words.contains(word)){
                    dp[i]=true;
                    break;
                }
            }
        }
        return dp[n];
    }
}

时间复杂度：$O(n^3)$，因为substring返回子串的副本是O(n)的复杂度（这里的n是substring的长度）
空间复杂度：$O(n)$

背包问题总结

动态规划五部曲，其中递推公式和确定遍历顺序最重要，因此从这两点对背包问题进行总结。

背包递推公式

问能否能装满背包（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ，对应题目如下：

• 动态规划：416.分割等和子集
• 动态规划：1049.最后一块石头的重量 II

问装满背包有几种方法：dp[j] += dp[j - nums[i]] ，对应题目如下：

• 动态规划：494.目标和
• 动态规划：518. 零钱兑换 II
• 动态规划：377.组合总和Ⅳ
• 动态规划：70. 爬楼梯进阶版（完全背包）

问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ，对应题目如下：

• 动态规划：474.一和零

问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ，对应题目如下：

• 动态规划：322.零钱兑换
• 动态规划：279.完全平方数

遍历顺序

01背包

• 二维dp数组01背包：先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。
• 一维dp数组01背包：只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

完全背包

纯完全背包的一维dp数组实现，先遍历物品还是先遍历背包都是可以的，且第二层for循环是从小到大遍历。

但是题目稍有变化，两个for循环的先后顺序就不一样了。

求组合数：外层for遍历物品（i），内层for遍历背包（j）。
求排列数：外层for遍历背包（j），内层for遍历物品（i）。

相关题目如下：

• 求组合数：动态规划：518.零钱兑换II
• 求排列数：动态规划：377. 组合总和 Ⅳ、动态规划：70.爬楼梯进阶版（完全背包）
• 求最小数：动态规划：322. 零钱兑换、动态规划：279.完全平方数

对于背包问题，难点其实在于遍历顺序上！一定要把遍历顺序弄清楚！

背包问题总结

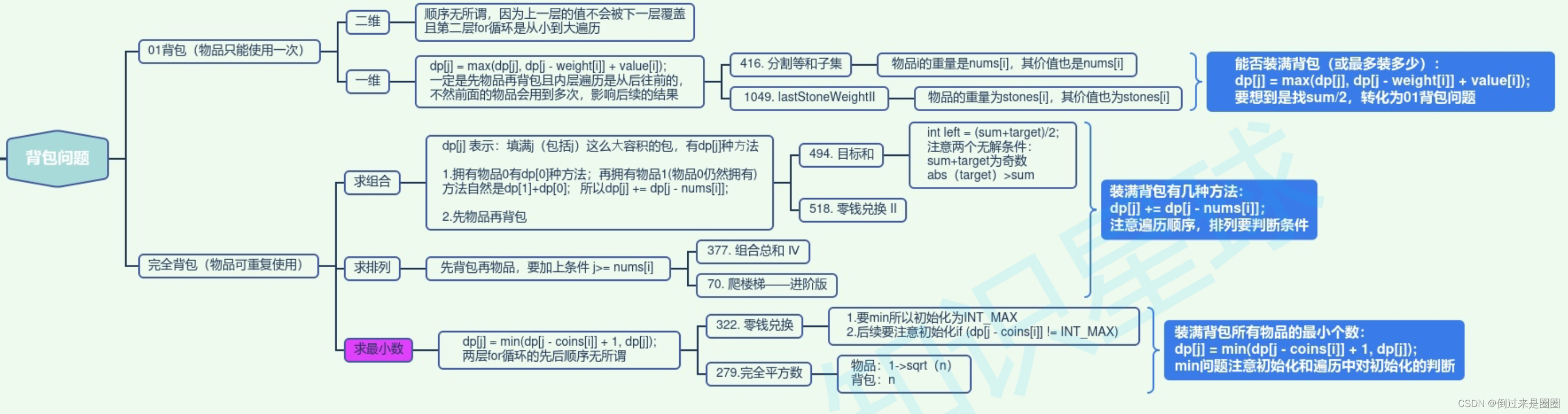
打家窃舍

198.打家劫舍
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。
 
题解

213.打家劫舍II
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。
 
题解

337.打家劫舍 III
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。
除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。
 
题解
树形dp入门题，使用长度为2的数组，记录当前节点偷与不偷所得到的最大金钱。

打家劫舍总结

劫舍系列简单来说就是 数组上连续元素二选一，成环之后连续元素二选一，在树上连续元素二选一，所能得到的最大价值。

股票问题

121. 买卖股票的最佳时机【简单】
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
 
题解：贪心 or 动规

122.买卖股票的最佳时机II【中等】
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
 
题解：贪心 or 动规
这里和121. 买卖股票的最佳时机唯一不同的地方，就是推导dp[i][0]的时候，第i天买入股票的情况。
因为股票全程只能买卖一次，所以如果买入股票，那么第i天持有股票即dp[i][0]一定就是 -prices[i]。
而本题，因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润。
那么第i天持有股票即dp[i][0]，如果是第i天买入股票，所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即：dp[i - 1][1] - prices[i]。

123.买卖股票的最佳时机III【困难】
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

188.买卖股票的最佳时机IV【困难】
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

309.最佳买卖股票时机含冷冻期【中等】
给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。​
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
 
题解
注意状态的转移：买入->卖出->冷冻期->买入，卖出和下一次买入之间必有一天冷冻期。

714.买卖股票的最佳时机含手续费【中等】
给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格；整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。
 
题解
几乎和 122.买卖股票的最佳时机II 一样。

股票问题总结：

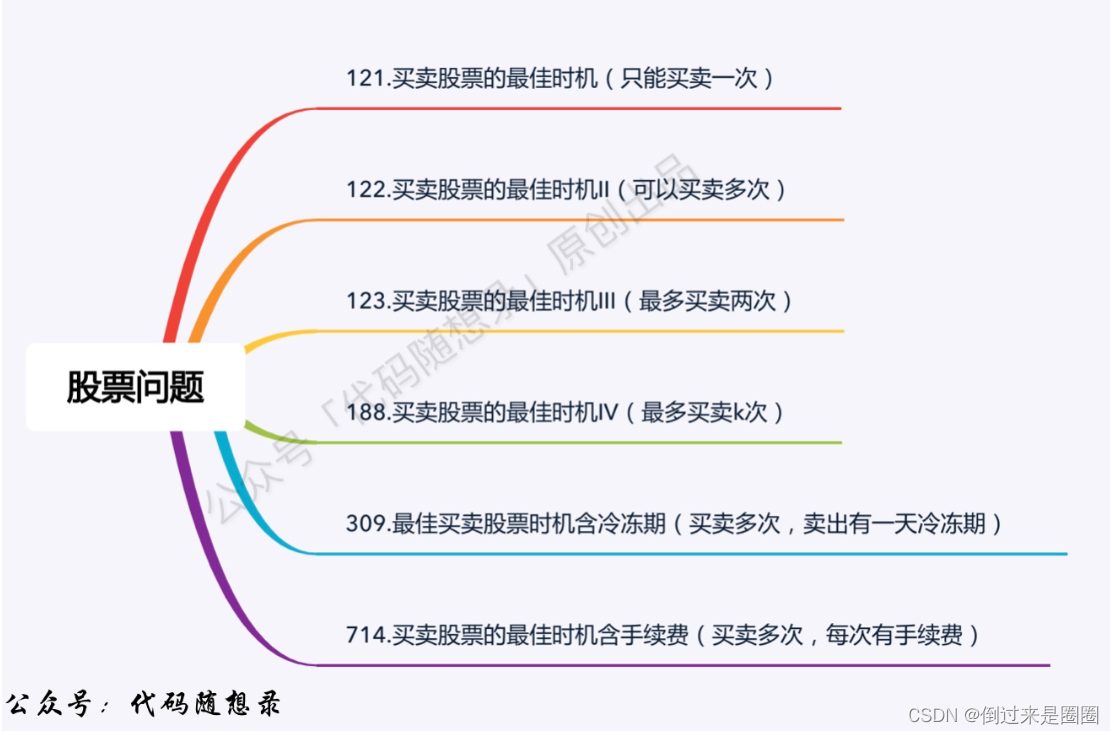
买卖股票的最佳时机III

123.买卖股票的最佳时机III【困难】

动态规划五部曲

买卖股票的最佳时机 I 是只买卖一次，买卖股票的最佳时机 II 是可以买卖多次，而本题是最多买卖两次。

1. 状态定义：
   每天有5个状态：
   （0）无操作（也可不设置）
   （1）第一次持有股票
   （2）第一次不持有股票
   （3）第二次持有股票
   （4）第二次不持有股票
   dp[i][j] 表示第 i 天状态 j 所剩最大现金。
2. 递推公式：
   达到dp[i][1]状态，有两个具体操作：
   （1）第 i 天买入股票了，dp[i][1]=dp[i-1][0]-prices[i]
   （2）第 i 天没有操作，dp[i][1]=dp[i-1][1]
   所以dp[i][1] = Math.max(dp[i-1][0]-prices[i] , dp[i-1][1])
   达到dp[i][2]状态，有两个具体操作：
   （1）第 i 天卖出股票了，dp[i][2]=dp[i-1][1]+prices[i]
   （2）第 i 天没有操作，dp[i][2]=dp[i-1][2]
   所以dp[i][2] = Math.max(dp[i-1][1]+prices[i] , dp[i-1][2])
   同理，dp[i][3] = Math.max(dp[i-1][2]-prices[i] , dp[i-1][3])
dp[i][4] = Math.max(dp[i-1][3]+prices[i] , dp[i-1][4])
3. 初始条件：
   （1）dp[0][0]=0，第0天无操作，现金为0
   （2）dp[0][1]=-prices[0]，第0天买入股票
   （3）dp[0][2]=0
   （4）dp[0][3]=-prices[0]，第0天第2次买入股票，没有第一次哪儿来的第二次呢？可以理解为第一次买股票，当天买当天卖，然后又买了一次
   （5）dp[0][4]=0
4. 遍历顺序：从前向后
5. 举例：以输入[1,2,3,4,5]为例
   

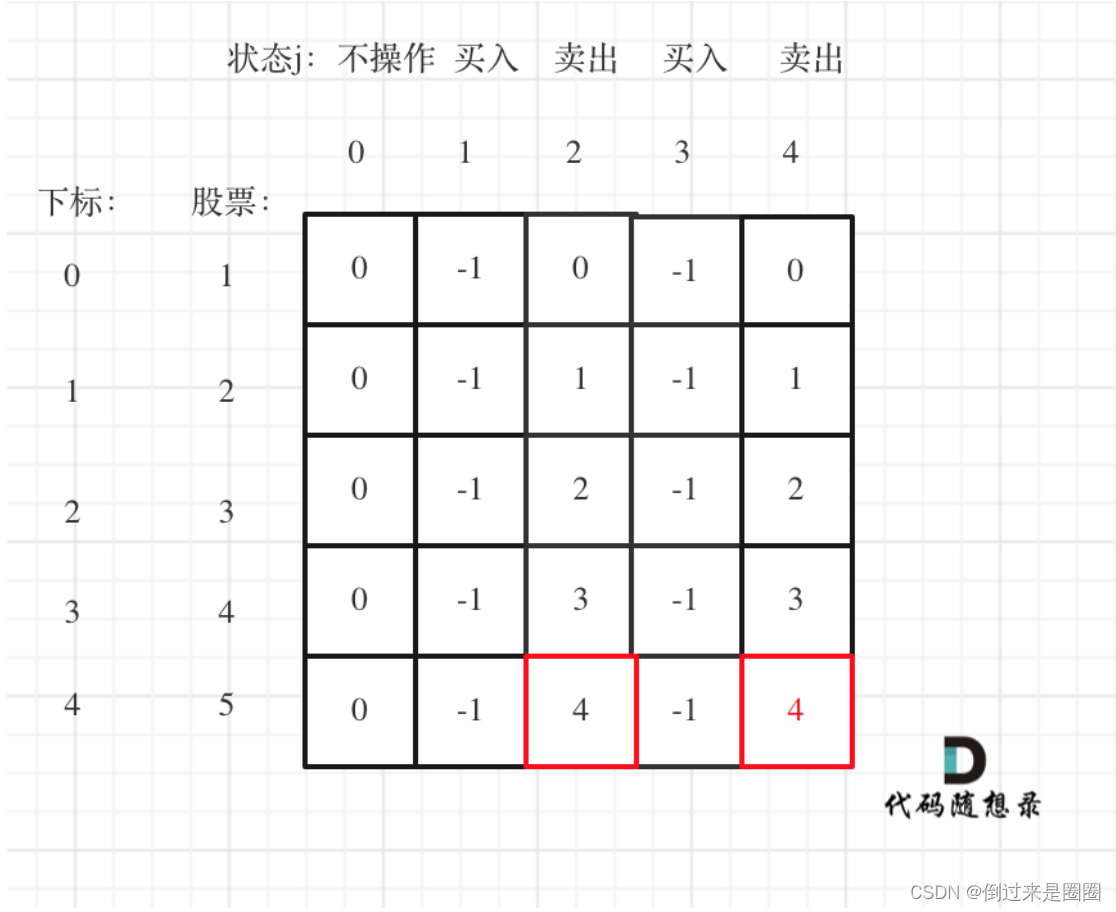
完整代码如下：

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        int[][] dp=new int[n][5];
        dp[0][1]=-prices[0];
        dp[0][3]=-prices[0];
        for(int i=1;i<n;i++){
            dp[i][1]=Math.max(dp[i-1][0]-prices[i] , dp[i-1][1]);
            dp[i][2] = Math.max(dp[i-1][1]+prices[i] , dp[i-1][2]);
            dp[i][3] = Math.max(dp[i-1][2]-prices[i] , dp[i-1][3]);
            dp[i][4] = Math.max(dp[i-1][3]+prices[i] , dp[i-1][4]);
        }
        return dp[n-1][4];
    }
}

时间复杂度：$O(n)$

空间复杂度：$O(n\times 5)$

买卖股票的最佳时机IV

188.买卖股票的最佳时机IV
给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

动态规划五部曲

和123.买卖股票的最佳时机III相比，交易的笔数从2笔改为k笔。

1. 状态定义：dp[i][j] 表示第 i 天状态 j 所剩最大现金。
   在买卖股票III中，dp有5个状态，那么本题中状态数可以增加到2k+1：
   （0）无操作（也可不设置）
   （1）第一次持有股票
   （2）第一次不持有股票
   （3）第二次持有股票
   （4）第二次不持有股票
   （5）…
   可以发现，除0之外，偶数就是不持有，奇数就是持有。所以 j 的范围在0到2k之间。
2. 递推公式：
   达到dp[i][1]状态，有两个具体操作：
   （1）第 i 天买入股票了，dp[i][1]=dp[i-1][0]-prices[i]
   （2）第 i 天没有操作，dp[i][1]=dp[i-1][1]
   所以dp[i][1] = Math.max(dp[i-1][0]-prices[i] , dp[i-1][1])
   达到dp[i][2]状态，有两个具体操作：
   （1）第 i 天卖出股票了，dp[i][2]=dp[i-1][1]+prices[i]
   （2）第 i 天没有操作，dp[i][2]=dp[i-1][2]
   所以dp[i][2] = Math.max(dp[i-1][1]+prices[i] , dp[i-1][2])
   同理类比剩下的状态，dp[i][j+1] = Math.max(dp[i-1][j]-prices[i] , dp[i-1][j+1])
dp[i][j+2] = Math.max(dp[i-1][j+1]+prices[i] , dp[i-1][j+2])
3. 初始条件：
   （1）dp[0][0]=0，第0天无操作，现金为0
   （2）dp[0][1]=-prices[0]，第0天买入股票
   （3）dp[0][2]=0
   （4）dp[0][3]=-prices[0]，第0天第2次买入股票，没有第一次哪儿来的第二次呢？可以理解为第一次买股票，当天买当天卖，然后又买了一次
   （5）dp[0][4]=0
   同理推出，当 j 为奇数时，dp[i][j]=-prices[0]
   初始化时类比，j 为奇数是买，偶数是卖的状态。
4. 遍历顺序：从前向后

完整代码如下：

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n=prices.length;
        if(n==0)
            return 0;
        int[][] dp=new int[n][2*k+1];
        for(int i=1;i<2*k;i+=2)
            dp[0][i]=-prices[0];
        for(int i=1;i<n;i++){
            for(int j=0;j<2*k-1;j+=2){
                dp[i][j+1]=Math.max(dp[i-1][j]-prices[i] , dp[i-1][j+1]);
                dp[i][j+2]=Math.max(dp[i-1][j+1]+prices[i] , dp[i-1][j+2]);
            }
        }
        return dp[n-1][2*k];
    }
}

时间复杂度：$O(n)$

空间复杂度：$O(n\times k)$

股票问题总结

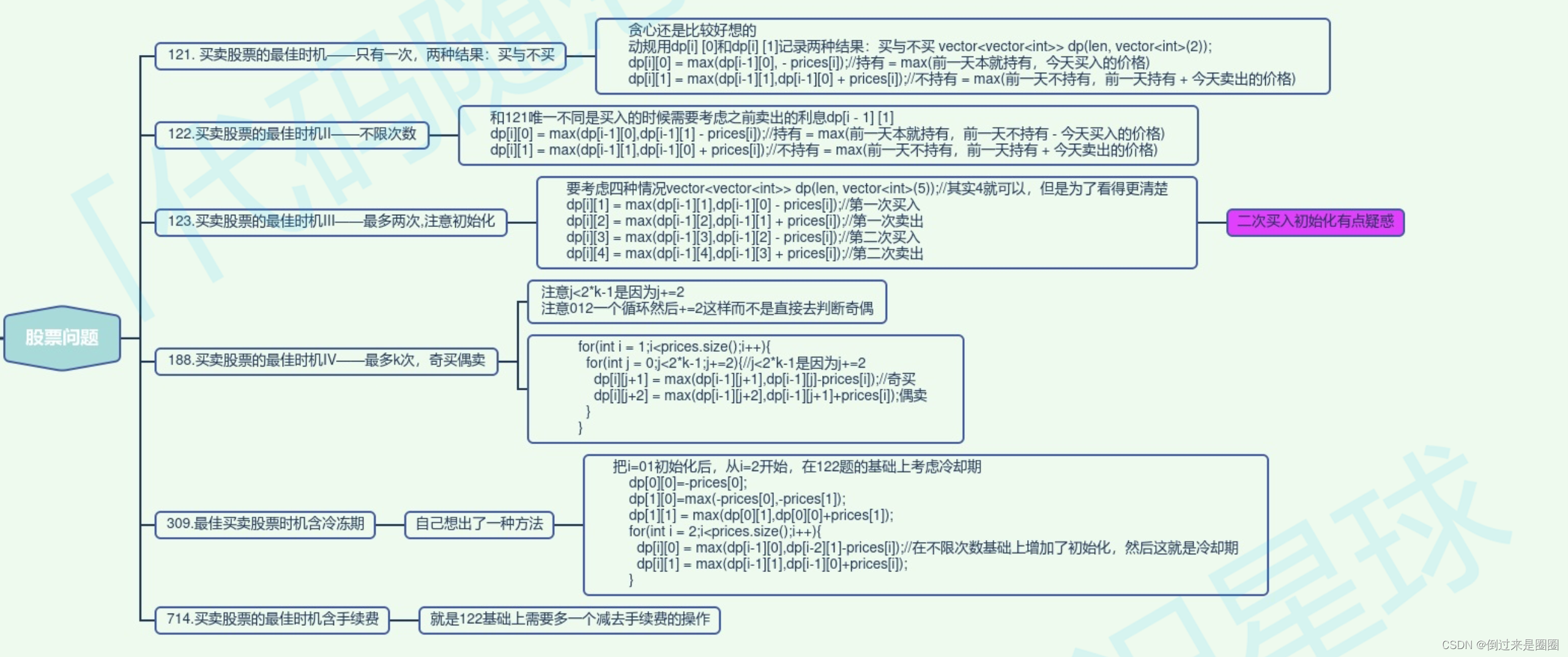
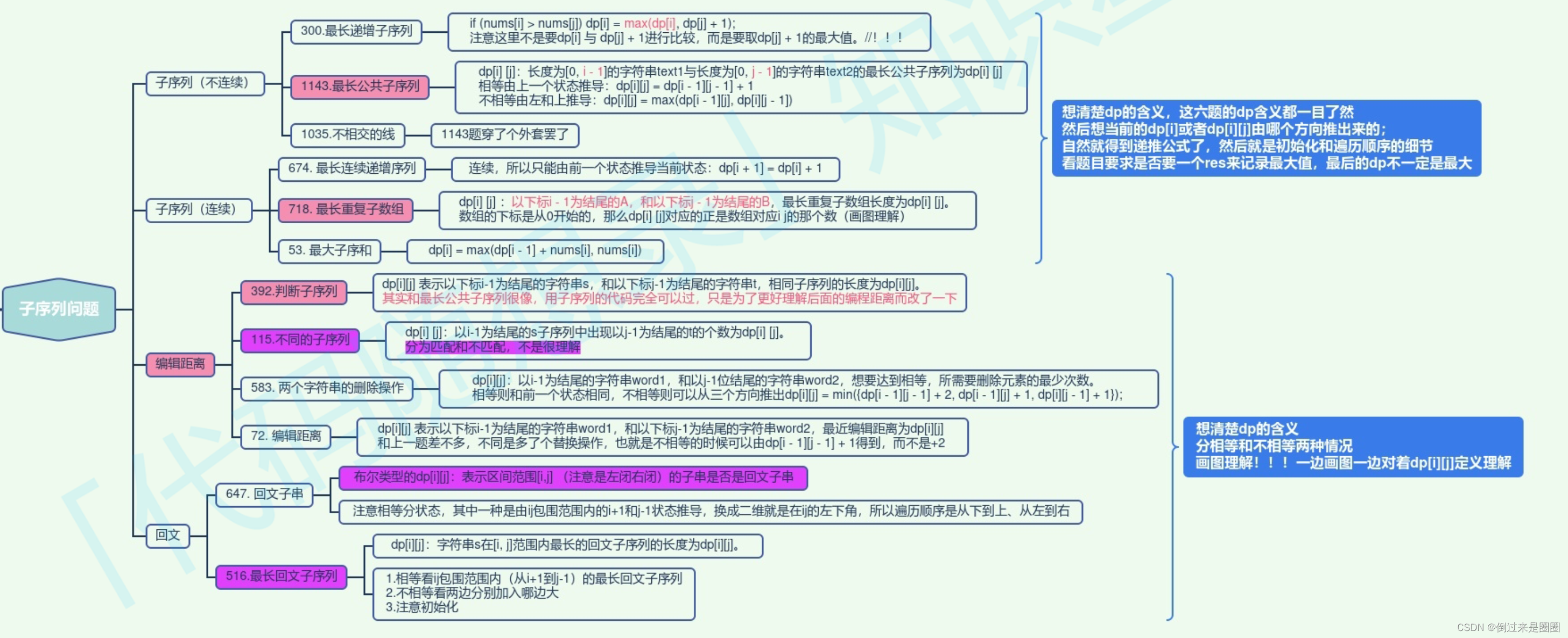
子序列问题

1. 最长上升子序列

300.最长递增子序列
给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

动态规划五部曲

1. 状态定义：dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。
2. 递推公式：dp[i]=j 从0到 i-1 各个位置的最长升序子序列+1的最大值。
   所以，if(nums[i]>nums[j]) dp[i]=max(dp[i],dp[j]+1)。
3. 初始条件：dp[i]=1，表示每个元素都至少可以单独成为子序列，此时长度为1。
4. 遍历顺序：dp[i]是由 0 到 i-1 各个位置的最长递增子序列推导而来，所以 i 一定是从前向后遍历。
   j 其实就是从0 遍历到 i-1，从前向后或者从后向前都无所谓，只要把 0~i-1 的元素都遍历了就行。所以使用默认习惯 从前向后 遍历。
5. 举例：输入：[0,1,0,3,2]，dp数组的变化如下，
   

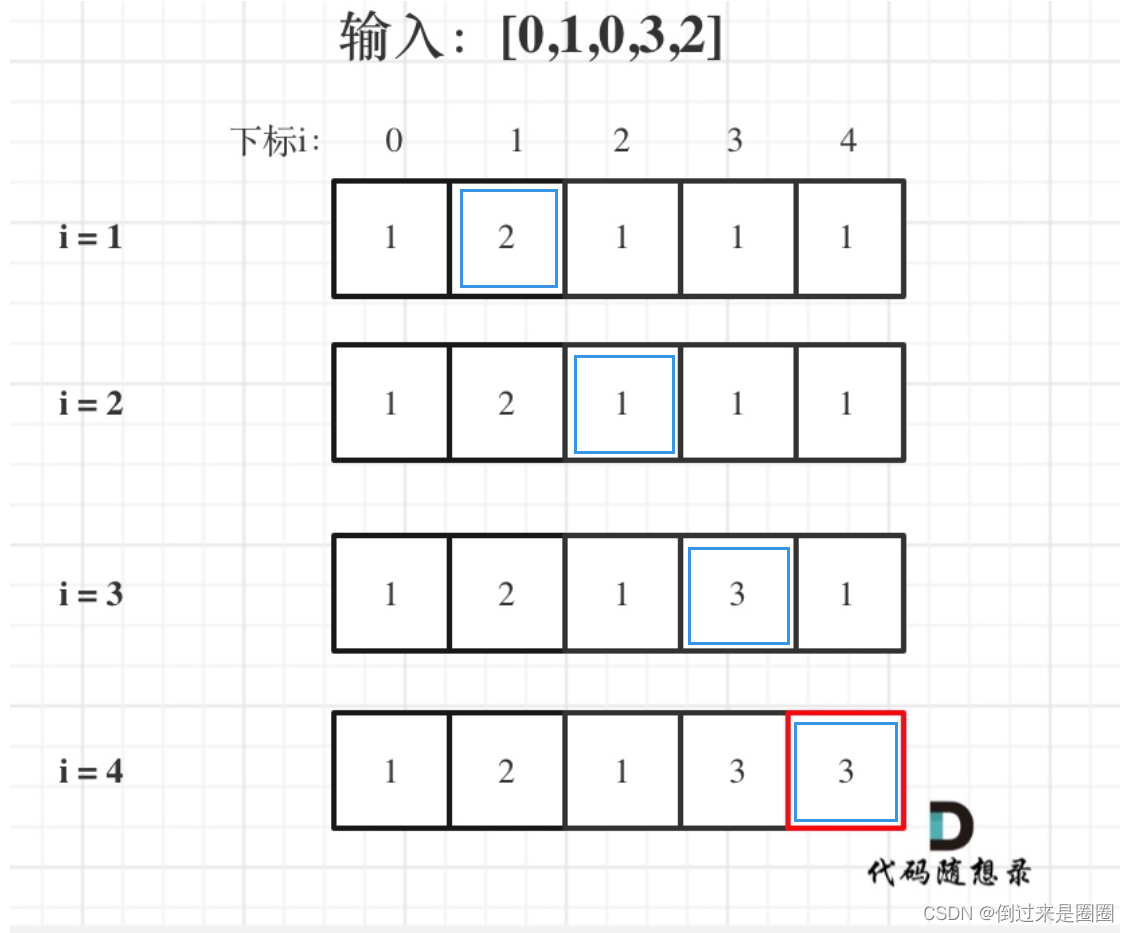
完整代码如下：

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n=nums.length,res=1;
        int[] dp=new int[n];
        Arrays.fill(dp,1);
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j])
                    dp[i]=Math.max(dp[i],dp[j]+1);
                res=Math.max(res,dp[i]);
            }
        }
        return res;
    }
}

时间复杂度：$O(n^2)$

空间复杂度：$O(n)$

2. 最长重复子数组

718. 最长重复子数组
给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

动态规划五部曲

注意题目中说的子数组，其实就是连续子序列。

1. 状态定义：dp[i][j]表示以下标 i - 1为结尾的A，和以下标 j - 1为结尾的B的最长重复子数组长度。
   （这里有一个问题是，为什么是下标i-1，而不是 i 呢？下面拓展进行解释
2. 递推公式：if(nums[i]==nums[j]) dp[i][j]=dp[i-1][j-1]+1。
   从公式中可以看出，遍历 i，j 要从1开始。
3. 初始条件：根据dp[i][j]定义，i或者j为0时是没有意义的，所以均初始化为0。
4. 遍历顺序：根据递推公式，只可能是从前向后遍历，至于for的内外层遍历哪个数组无所谓。
5. 举例：A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，dp状态如下，
   
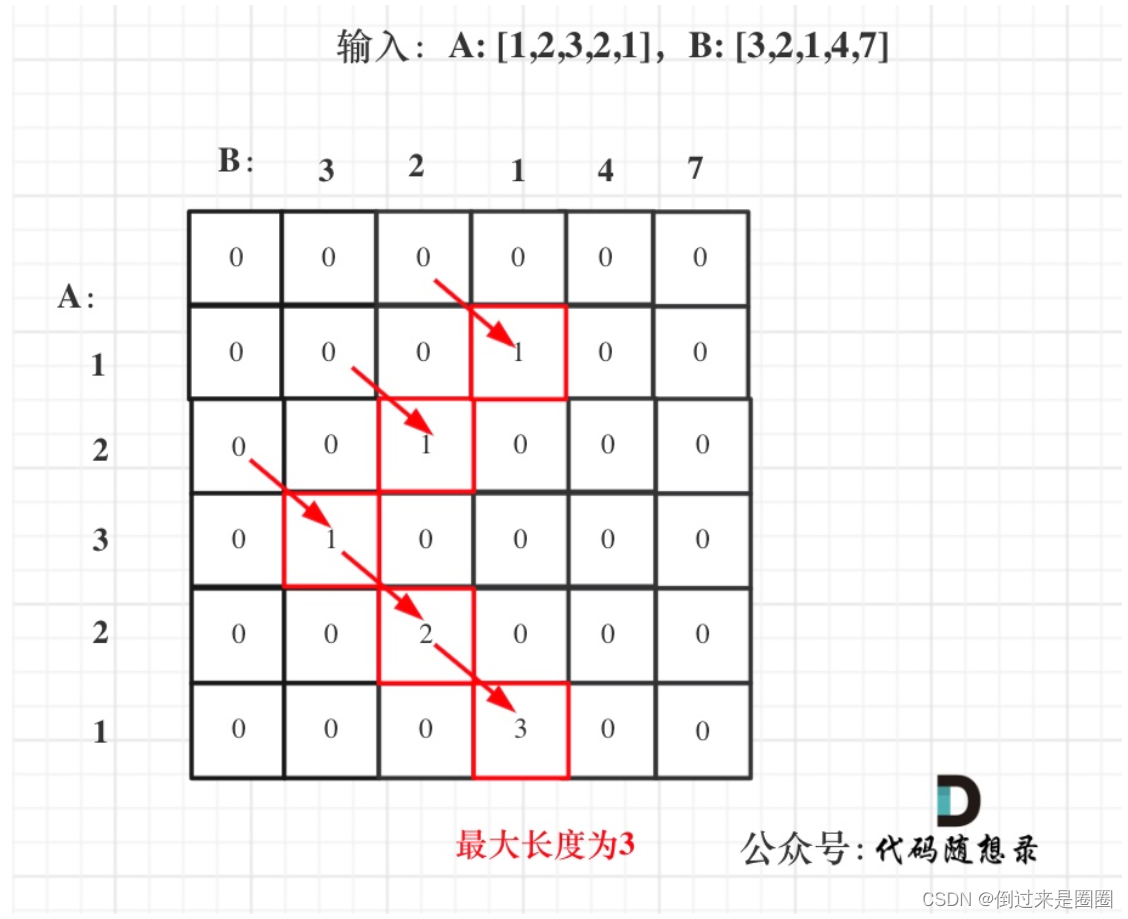
   完整代码如下：

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int n1=nums1.length,n2=nums2.length,res=0;
        int[][] dp=new int[n1+1][n2+1];
        for(int i=1;i<=n1;i++){//注意i,j的范围是从1到n
            for(int j=1;j<=n2;j++){
                if(nums1[i-1]==nums2[j-1])
                    dp[i][j]=dp[i-1][j-1]+1;
                res=Math.max(res,dp[i][j]);//记录最大值
            }
        }
        return res;
    }
}

时间复杂度：$O(n1\ast n2)$

空间复杂度：$O(n1\ast n2)$，亦可以用滚动数组进行空间优化，但是要注意使用滚动数组时，内循环要从后向前遍历，避免重复覆盖。

拓展

为什么dp的定义中用 i-1和 j-1，而不是 i和 j？

• 可以定义为 i和 j，但是初始化过程会更麻烦
• 如果定义为 i和 j的话，第一行和第一列要进行初始化，那么如果nums1[i] 与 nums2[0] 相同的话，对应的 dp[i][0]就要初始为1，nums2[j] 与 nums1[0]相同的话，同理。
• 所以，如果定义为 i和 j的话，要加两个for循环对dp第一行第一列进行初始化。在递推公式中，还要加上 i和 j是否>0的条件判断。

3. 最长公共子序列

1143. 最长公共子序列
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

动态规划五部曲

本题和 718. 最长重复子数组 区别在于这里不要求是连续的了。

1. 状态定义：dp[i][j]表示[0, i - 1]的字符串text1，和[0, j - 1]的字符串text2的最长公共子序列长度。
2. 递推公式：
   （1）如果text1[i-1]==text2[j-1]：找到了一个公共元素，dp[i][j]=dp[i-1][j-1]+1；
   （2）如果text1[i-1]!=text2[j-1]：看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的，即dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])；
3. 初始条件：根据dp[i][j]定义，i或者j为0时是没有意义的，所以均初始化为0。
4. 遍历顺序：从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图，
   
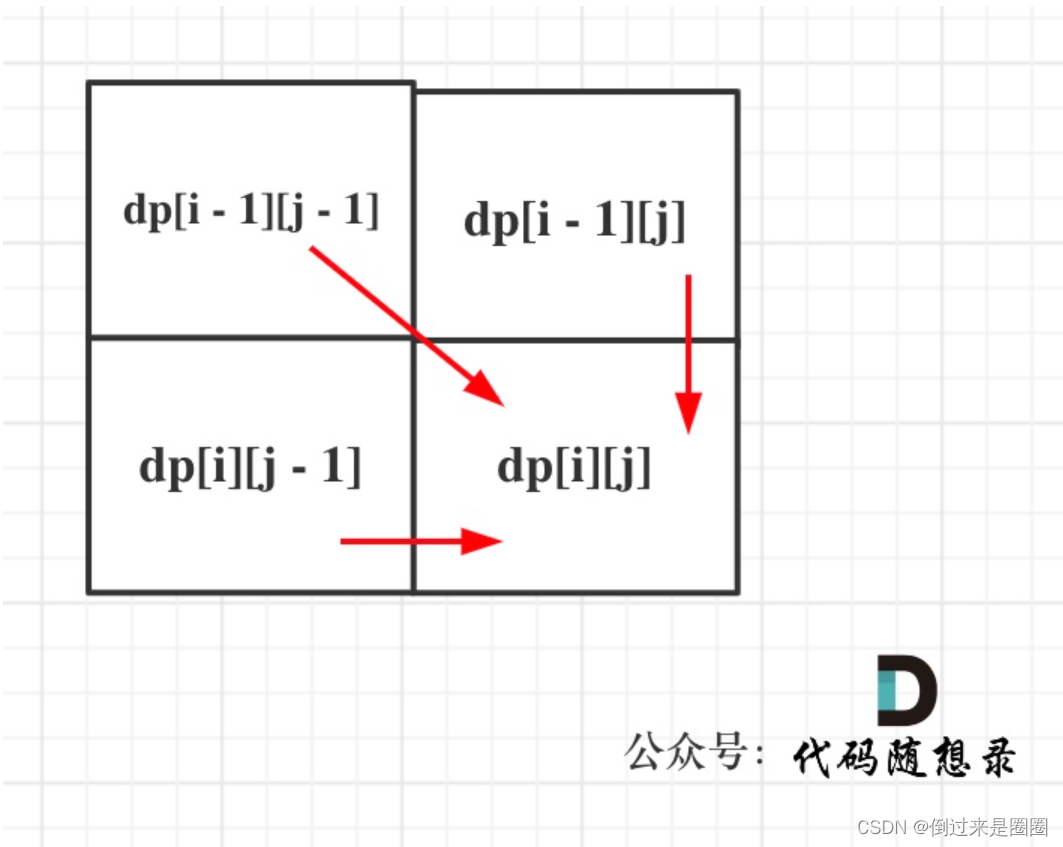
   那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。
5. 举例：text1 = “abcde”, text2 = “ace” 为例，dp状态如下，
   
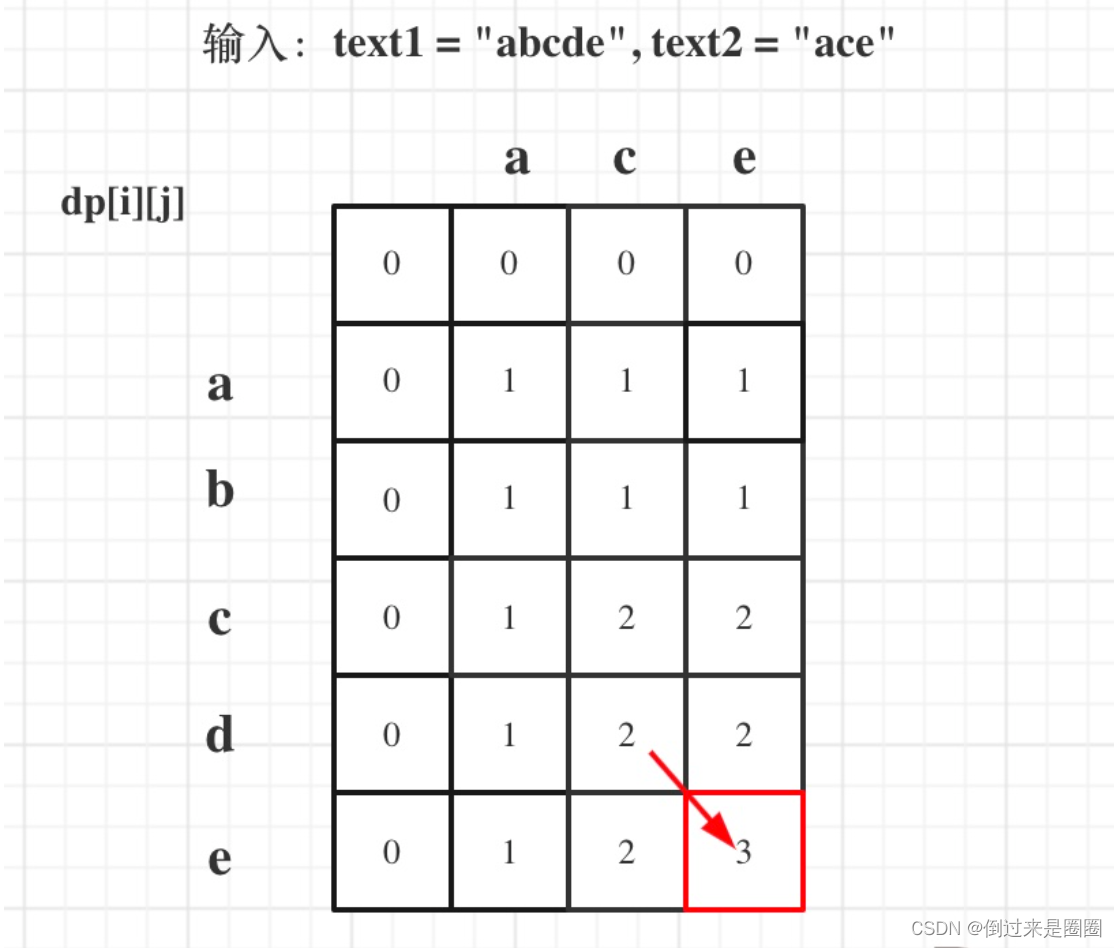
   完整代码如下：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int n1=text1.length(),n2=text2.length(),res=0;
        int[][] dp=new int[n1+1][n2+1];
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
            	//相等
                if(text1.charAt(i-1)==text2.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1]+1;
                //不等
                else
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[n1][n2];
    }
}

时间复杂度：$O(n1\ast n2)$

空间复杂度：$O(n1\ast n2)$

4. 不相交的线

1035.不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

• nums1[i] == nums2[j]
• 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

思路

绘制一些连接两个数字 A[i] 和 B[j] 的直线，只要 A[i] == B[j]，且直线不能相交！

直线不能相交，这就是说明在字符串A中 找到一个与字符串B相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，连接相同数字的直线就不会相交。

拿示例一A = [1,4,2], B = [1,2,4]为例，情况如图：

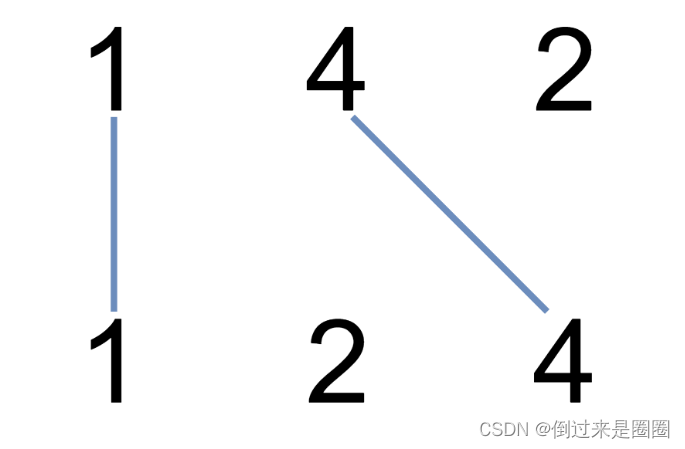
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

所以本题和上一题1143. 最长公共子序列相同，只需把字符串换成数组即可。

完整代码如下：

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m=nums1.length,n=nums2.length;
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(nums1[i-1]==nums2[j-1])
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[m][n];
    }
}

时间复杂度：$O(n1\ast n2)$

空间复杂度：$O(n1\ast n2)$

5. 最大子序和

53. 最大子数组和
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

动态规划五部曲

1. 状态定义：dp[i]表示以nums[i]为结尾的最大连续子序列和。
2. 递推公式：
   dp[i]只有两个方向可以推出来：
   （1）dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
   （2）nums[i]，即：从头开始计算当前连续子序列和
   所以dp[i] = max(dp[i - 1] + nums[i], nums[i])

其他条件比较简单，就不一一说了，完整代码如下：

class Solution {
    public int maxSubArray(int[] nums) {
        int n=nums.length,res=nums[0];
        int[] dp=new int[n];
        dp[0]=nums[0];
        for(int i=1;i<n;i++){
            dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
            res=Math.max(res,dp[i]);
        }
        return res;
    }
}

时间复杂度：$O(n)$

空间复杂度：$O(n)$

6. 判断子序列

392.判断子序列
给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：
如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

动态规划五部曲

编辑距离的入门题目！只计算删除，而不用考虑增加和替换的情况。

1. 状态定义：dp[i][j]表示以下标 i-1为结尾的字符串s，和以下标 j-1为结尾的字符串t，相同子序列的长度。
2. 递推公式：
   考虑两种操作：
   （1）s[i - 1] == t[j - 1]：dp[i][j] = dp[i - 1][j - 1] + 1
   （2）s[i - 1] != t[j - 1]：此时 t 要删元素，所以dp[i][j] = dp[i][j - 1]
   这里与 1143. 最长公共子序列 的递推公式基本一致，区别就是本题删除的一定是字符串 t ，而1143是两个字符串都可以删除。
3. 初始条件：从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以dp[0][0]和dp[i][0]是一定要初始化的。均初始化为0。
4. 遍历顺序：从递推公式，可以看出，dp[i - 1][j - 1] 和 dp[i][j - 1]可以推出dp[i][j]，如图，
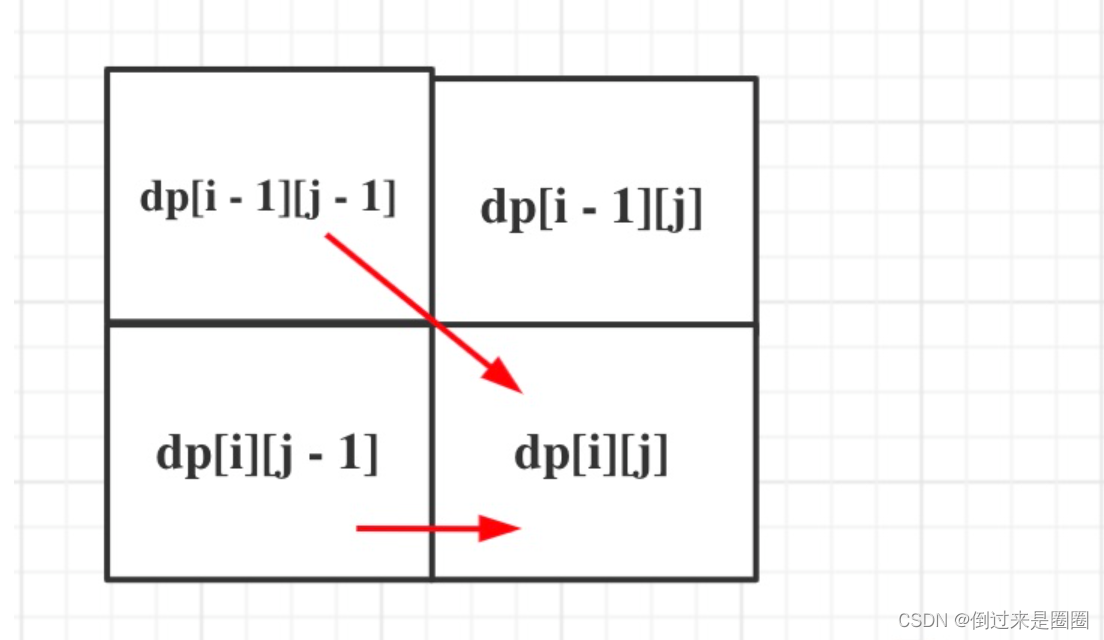   5. 举例：输入：s = “abc”, t = “ahbgdc”，dp状态转移图如下，
   

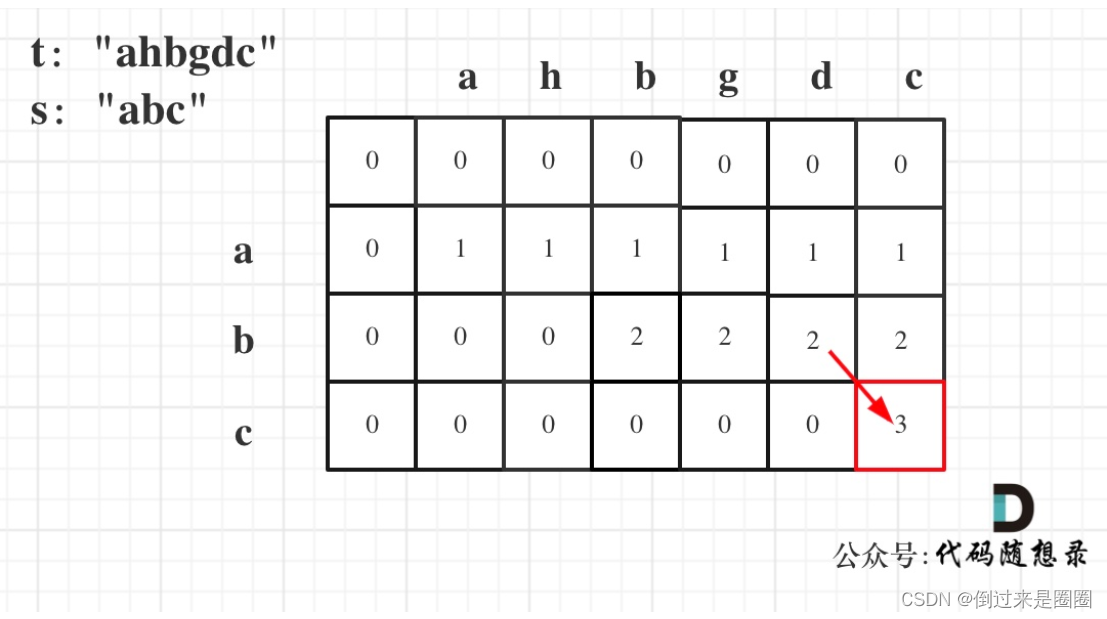
完整代码如下：（本题也可以用贪心+双指针做）

class Solution {
    public boolean isSubsequence(String s, String t) {
        int m=s.length(),n=t.length();
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(s.charAt(i-1)==t.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=dp[i][j-1];
            }
        }
        return dp[m][n]==m;
    }
}

时间复杂度：$O(n\ast m)$

空间复杂度：$O(n\ast m)$

7. 不同的子序列

115. 不同的子序列【困难】
给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，“ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

动态规划五部曲

如果不是子序列，而是连续子序列，可以考虑用KMP。

1. 状态定义：dp[i][j]表示以下标 i-1为结尾的字符串s中，出现以下标 j-1为结尾的字符串t 的个数。
2. 递推公式：
   考虑两种操作：
   （1）s[i - 1] == t[j - 1]：dp[i][j] = dp[i - 1][j - 1] + dp[i -1][j]
   （2）s[i - 1] != t[j - 1]：dp[i][j] = dp[i -1][j]，相当于在s中删除s[i-1]再进行匹配
3. 初始条件：从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i -1][j]，所以dp[0][0]和dp[0][j]是一定要初始化的。
   （1）dp[i][0]表示什么呢？以s[i-1]结尾的s中，出现空字符串的个数，所以初始化为1。
   （2）dp[0][j]表示什么呢？在空字符串中出现以t[j-1]为结尾的t的个数，那必然是0。
   （3）dp[0][0]表示什么呢？空字符串s，可以删除0个元素，变成空字符串t，所以初始化为1。
4. 遍历顺序：从递推公式，可以看出，dp[i - 1][j - 1] 和 dp[i ][j - 1]可以推出dp[i][j]，如图，
   
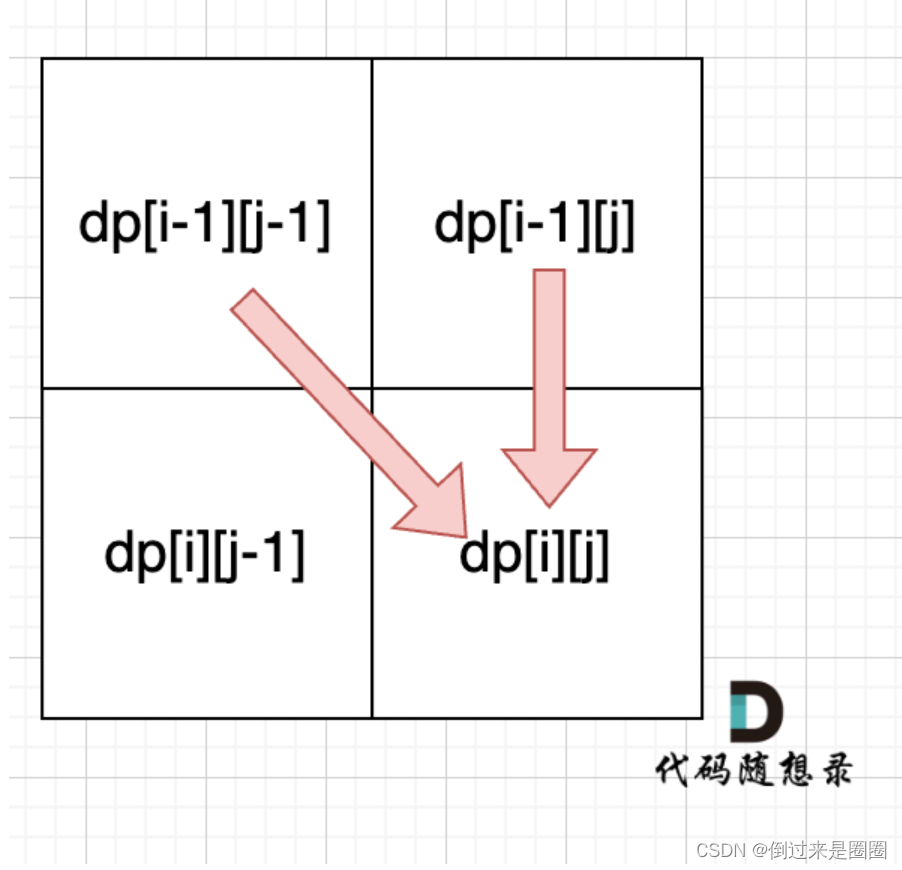
5. 举例：以s：“baegg”，t："bag"为例，推导dp数组状态如下，
   
   dp[5][4]为例，即图中红框格，dp[5][4]=d[4][3]+dp[4][4]，即baeg(s)中ba(t)的个数+baeg(s)中bag(t)的个数。

完整代码如下：

class Solution {
    public int numDistinct(String s, String t) {
        int m=s.length(),n=t.length();
        int[][] dp=new int[m+1][n+1];
        //dp初始化
        for(int i=0;i<=m;i++)
            dp[i][0]=1;
        //递推公式
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(s.charAt(i-1)==t.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                else
                    dp[i][j]=dp[i-1][j];
            }
        }
        return dp[m][n];
    }
}

8. 两个字符串的删除操作

583. 两个字符串的删除操作【中等】
给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

动态规划五部曲

和上一题115. 不同的子序列相比，两个字符串都可以删除了，而115题仅可以删除源字符串s中的字符。

1. 状态定义：dp[i][j]表示以下标 i-1为结尾的字符串word1，和以下标 j-1为结尾的字符串 word2 ，想要达到相等，所需要删除元素的最少次数。
2. 递推公式：
   考虑两种操作：
   （1）word1[i - 1] == word2[j - 1]：dp[i][j] = dp[i - 1][j - 1]。
   （2）word1[i - 1] != word2[j - 1]：有以下三种情况，
   情况一：删word1[i-1]，最少操作次数为dp[i -1][j]+1；
   情况二：删word2[j-1]，最少操作次数为dp[i][j-1]+1；
   情况三：同时删word1[i - 1]和word2[j - 1]，最少操作次数为dp[i - 1][j - 1] + 2；
   所以最终dp[i][j]取三种情况中的最小值，即dp[i][j]=min(dp[i -1][j]+1 , dp[i][j-1]+1 , dp[i - 1][j - 1] + 2)；
   由于 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2（因为在删掉word2[j-1]的基础上加一步操作，跟删掉word2[j-1]和word1[i-1]再加两步的操作数是一样的），所以递推公式可简化为：dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
3. 初始条件：从递推公式可以看出dp[i][j]都是依赖于dp[i][j - 1] 和 dp[i -1][j]，所以dp[i][0]和dp[0][j]是一定要初始化的。
   （1）dp[i][0]表示什么呢？word2是空字符串，以s[i-1]结尾的word1要删掉多少个字符才可以变成空字符串，所以初始化为i。
   （2）dp[0][j]表示什么呢？同理，初始化为j。
4. 遍历顺序：从递推公式，可以看出，dp[i - 1][j] 和 dp[i][j - 1]可以推出dp[i][j]，所以遍历顺序一定是从上到下，从左到右。
5. 举例：以word1:“sea”，word2:"eat"为例，推导dp数组状态图如下，
   

完整代码如下：

class Solution {
    public int minDistance(String word1, String word2) {
        int m=word1.length(),n=word2.length();
        //dp初始化
        int[][] dp=new int[m+1][n+1];
        for(int i=0;i<=m;i++)
            dp[i][0]=i;
        for(int j=1;j<=n;j++)
            dp[0][j]=j;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1];//不用删
                else
                    dp[i][j]=Math.min(dp[i-1][j]+1,dp[i][j-1]+1);//两个单词中删一个字符，选小的
            }
        }
        return dp[m][n];
    }
}

9. 编辑距离

72. 编辑距离
给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

动态规划五部曲

1. 状态定义：dp[i][j] 表示 word1 的前 i 个字母（下标为 i-1）和 word2 的前 j 个字母之间的编辑距离。

2. 递推公式：
   考虑两种操作：
   （1）word1[i - 1] == word2[j - 1]：dp[i][j] = dp[i - 1][j - 1]，即不用编辑。
   （2）word1[i - 1] != word2[j - 1]：有以下三种情况，
   情况一：删word1[i-1]，最少操作次数为dp[i -1][j]+1；
   情况二：删word2[j-1]，最少操作次数为dp[i][j -1]+1；
   情况三：替换word1[i - 1]，使其与word2[j - 1]相同，最少操作次数为dp[i - 1][j - 1] + 1；
   所以最终dp[i][j]取三种情况中的最小值，即dp[i][j]=min(dp[i-1][j] , dp[i][j-1] , dp[i - 1][j - 1])+1；

3. 初始条件：
   （1）dp[i][0]表示什么呢？以s[i-1]结尾的word1，和空字符串之间的编辑距离，word1删除i个字符即可得到空串，所以初始化为i。
   （2）dp[0][j]表示什么呢？同理，初始化为j。

4. 遍历顺序：从递推公式，可以看出，遍历顺序一定是从上到下，从左到右。
   

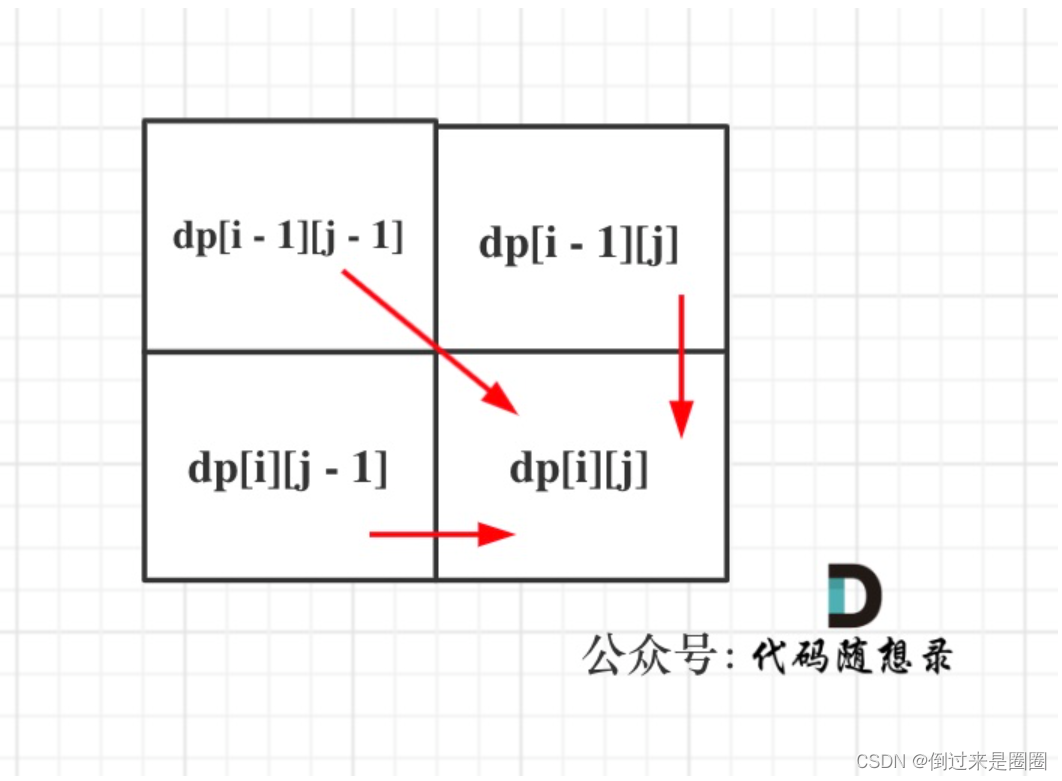
5. 举例：以word1 = “horse”, word2 = "ros"为例，推导dp数组状态图如下，
   

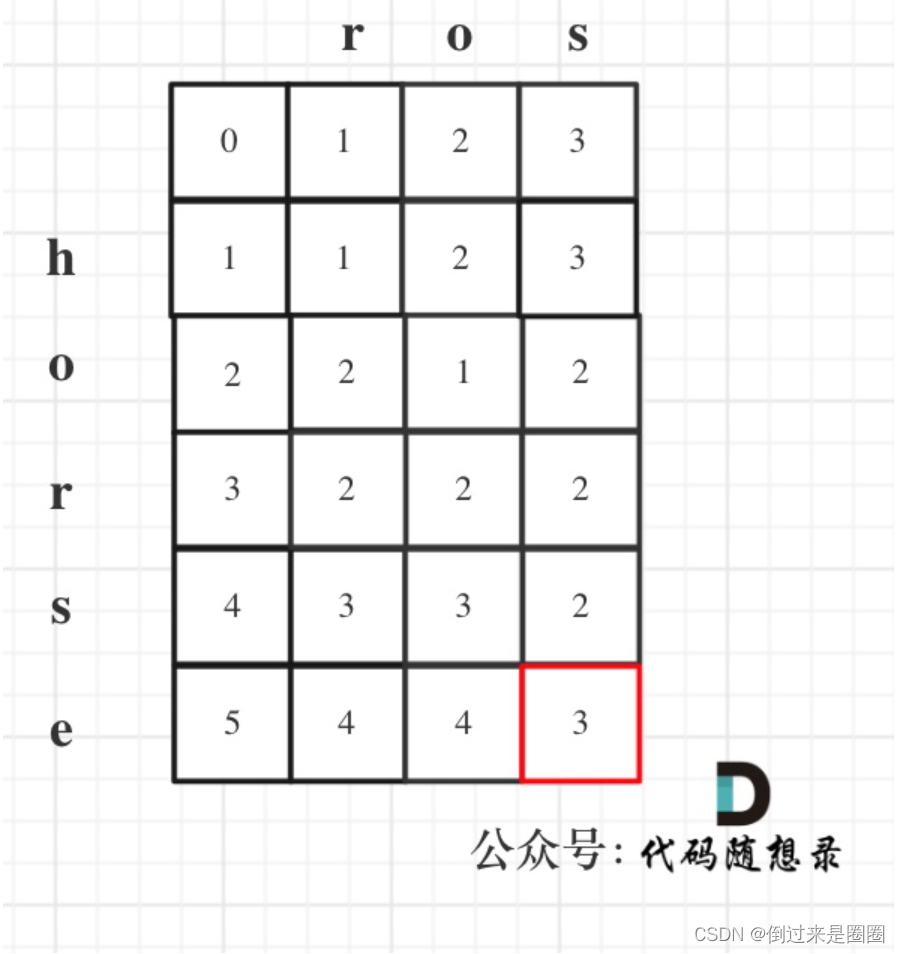
完整代码如下：

class Solution {
    public int minDistance(String word1, String word2) {
        int m=word1.length(),n=word2.length();
        int[][] dp=new int[m+1][n+1];
        for(int i=0;i<=m;i++)
            dp[i][0]=i;
        for(int j=1;j<=n;j++)
            dp[0][j]=j;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1];
                else
                    dp[i][j]=Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1]))+1;
            }
        }
        return dp[m][n];
    }
}

p.s 第一遍做的时候的笔记写的更细致点，思路是按照官解来的，和代码随想录的不太一样。

10. 回文子串

647. 回文子串
给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

动态规划五部曲

1. 状态定义：dp[i][j] 表示区间范围[i,j] （左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。
2. 递推公式：
   （1）s[i] != s[j]：dp[i][j] = false，必然不是回文子串。
   （2）s[i] == s[j]：分为以下三种情况，
   情况1：i==j，只有一个字符a，dp[i][j]=true；
   情况2：j==i+1，两个相邻字符aa，dp[i][j]=true；
   情况3：j>i+1，例如cabac，此时dp[i][j]=dp[i+1][j-1]。
3. 初始条件：刚开始肯定没有匹配，dp[i][j]=false。
4. 遍历顺序：从递推公式，可以看出，dp[i][j]是由左下角推出的，因此遍历顺序一定为从下到上，从左到右。
   

完整代码如下：

class Solution {
    public int countSubstrings(String s) {
        int n=s.length(),res=0;
        boolean[][] dp=new boolean[n][n];
        for(int i=n-1;i>=0;i--){//从下到上
            for(int j=i;j<n;j++){
                if(s.charAt(i)==s.charAt(j)){
                    if((i==j)||(j==i+1)||(dp[i+1][j-1])){
                        res++;
                        dp[i][j]=true;
                    }   
                }//s[i]!=s[j]时,dp默认为false,因此不用再讨论
            }
        }
        return res;
    }
}

p.s 另外一种双指针的方法见【LeetCode】Day151-回文子串，空间复杂度更小。

11. 最长回文子序列

516.最长回文子序列【中等】
给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

动态规划五部曲

上一题647. 回文子串，求的是回文子串，而本题求的是回文子序列。

回文子串是连续的，而回文子序列不是连续的！

思路差不多，但是本题比回文子串情况少了一点，因此要简单一些。

1. 状态定义：dp[i][j] 表示字符串s在[i, j]范围内最长的回文子序列的长度。

2. 递推公式：
   （1）s[i]== s[j]：dp[i][j]=dp[i+1][j-1]+2
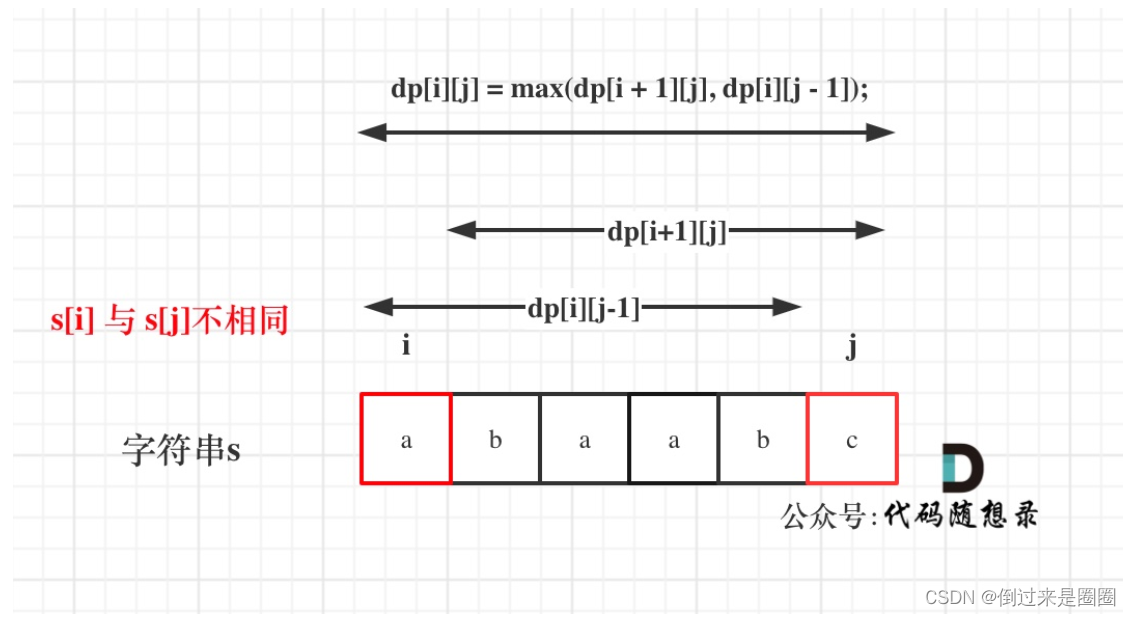
   （2）s[i] != s[j]：说明同时加入s[i]和s[j]不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]，看看哪一个可以组成最长的回文子序列。
   情况1：加入 s[j] 的回文子序列长度为dp[i+1][j]；
   情况2：加入 s[i] 的回文子序列长度为dp[i][j-1]；
   因此，此时dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
   

3. 初始条件：dp[i][i]=1，一个字符的回文子序列长度就是1。

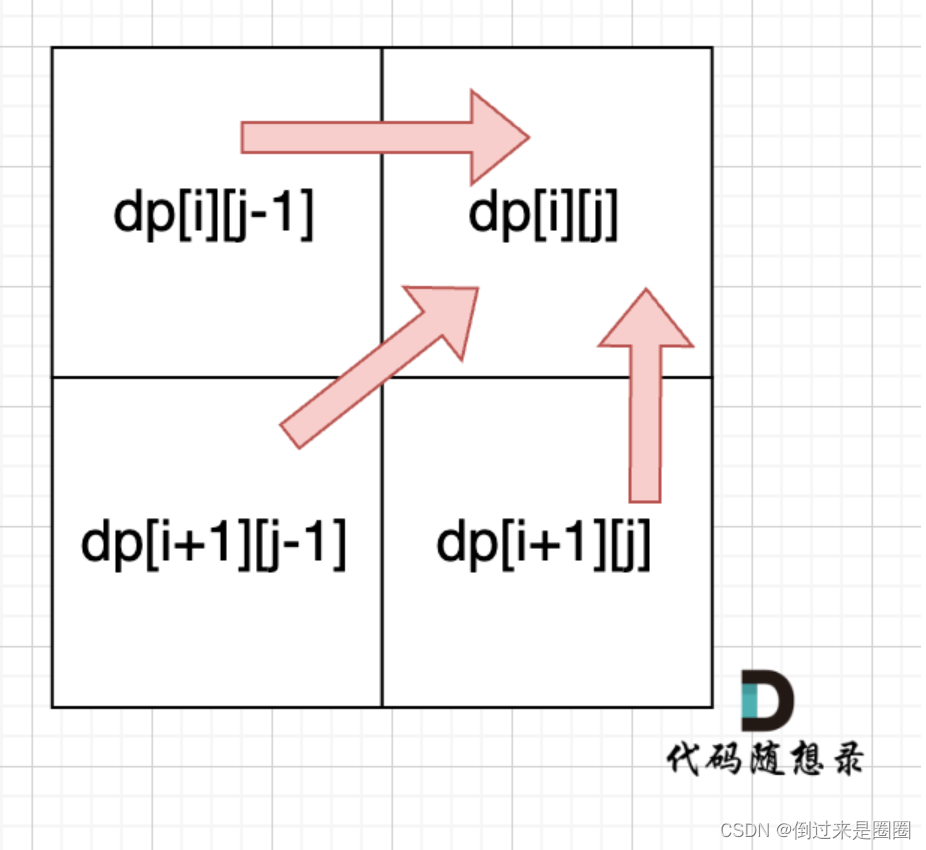
4. 遍历顺序：从递推公式，可以看出，dp[i][j]依赖于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]，因此遍历顺序一定为从下到上，从左到右。
   

5. 举例：输入s:“cbbd” 为例，dp数组状态如图，
   

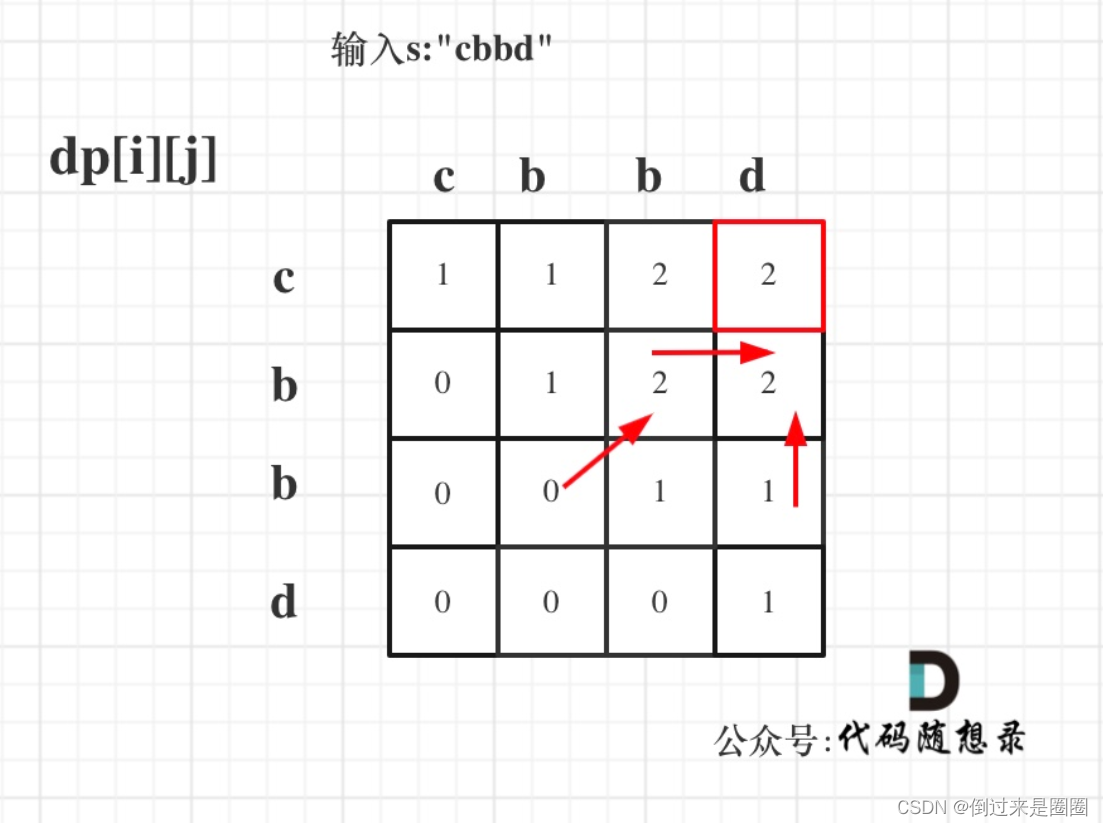
完整代码如下：

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n=s.length(),res=1;
        int[][] dp=new int[n][n];
        for(int i=n-1;i>=0;i--){
            dp[i][i]=1;//初始化
            for(int j=i+1;j<n;j++){
                char a=s.charAt(i),b=s.charAt(j);
                if(a==b)
                    dp[i][j]=dp[i+1][j-1]+2;
                else
                    dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);
            }
        }
        return dp[0][n-1];
    }
}

子序列问题总结

p.s 历时14天，终于把代码随想录的动态规划模块给过完啦！