文章目录
- 1 Probability and Statistics
- 2 Linear Algebra
- 3.Calculus
- 一览图
- hw0题目链接
1 Probability and Statistics
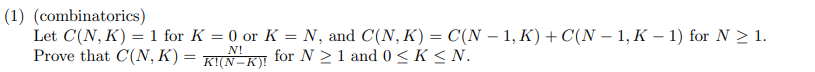
不妨假设
C
(
n
,
K
)
=
C
(
n
,
K
)
,
0
≤
K
≤
N
C(n, K)=C(n, K) ,0 \le K\le N
C(n,K)=C(n,K),0≤K≤N成立,只需证明
C
(
n
+
1
,
K
)
=
(
n
+
1
)
!
K
!
(
n
−
K
+
1
)
!
,
0
≤
K
≤
N
C(n+1, K)=\frac {(n+1)!}{K!(n-K+1)!} ,0 \le K\le N
C(n+1,K)=K!(n−K+1)!(n+1)!,0≤K≤N即可
- K=0, C ( n + 1 , K ) = 1 C(n+1, K)=1 C(n+1,K)=1,符合假设
- 1 ≤ K ≤ n 1\le K\le n 1≤K≤n,如下
C
(
n
+
1
,
K
)
=
C
(
n
,
K
)
+
C
(
n
,
K
−
1
)
=
n
!
K
!
(
n
−
K
)
!
+
n
!
(
K
−
1
)
!
(
n
−
K
+
1
)
!
=
n
!
(
n
−
K
+
1
+
K
)
K
!
(
n
−
K
+
1
)
!
=
n
!
(
n
+
1
)
K
!
(
n
−
K
+
1
)
!
=
(
n
+
1
)
!
K
!
(
n
−
K
+
1
)
!
\begin{aligned}C(n+1, K)&=C(n, K)+C(n,K-1)\\&=\frac {n!}{K!(n-K)!}+ \frac {n!}{(K-1)!(n-K+1)!}\\&=\frac {n!(n-K+1 + K)}{K!(n-K+1)!}\\&=\frac {n!(n+1)}{K!(n-K+1)!}\\&=\frac {(n+1)!}{K!(n-K+1)!}\end{aligned}
C(n+1,K)=C(n,K)+C(n,K−1)=K!(n−K)!n!+(K−1)!(n−K+1)!n!=K!(n−K+1)!n!(n−K+1+K)=K!(n−K+1)!n!(n+1)=K!(n−K+1)!(n+1)!
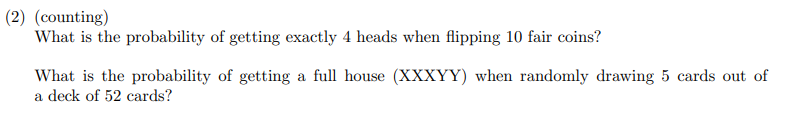
- 10次硬币4次正面 C 10 4 2 10 = 105 512 \frac{C_{10}^{4}}{2^{10}}=\frac {105}{512} 210C104=512105
- 13组,选2组进行组合
13
×
12
×
C
4
3
×
C
4
2
C
52
5
=
6
4165
\frac {13\times 12 \times C_4^3 \times C_4^2}{C_{52}^5}=\frac {6}{4165}
C52513×12×C43×C42=41656

- P ( 三次投掷有一次正面) = 1 − 1 8 = 7 8 P(三次投掷有一次正面)=1-\frac{1}{8}=\frac{7}{8} P(三次投掷有一次正面)=1−81=87
-
P
(
三次投掷有三次次正面)
=
1
8
P(三次投掷有三次次正面)=\frac{1}{8}
P(三次投掷有三次次正面)=81
p = 1 8 7 8 = 1 7 \mathbb p=\frac{\frac{1}{8}}{\frac{7}{8}}=\frac{1}{7} p=8781=71

- 随机位为0应该题目写错了,理解为大于小于0即可
令 A = { ∣ X ∣ = 1 } B = { X < 0 } \begin{aligned}A&=\{|X| =1 \}\\B&=\{X<0 \}\end{aligned} AB={∣X∣=1}={X<0}
则
p
=
P
(
B
∣
A
)
=
P
(
A
B
)
P
(
A
)
=
P
(
X
=
−
1
)
P
(
∣
X
∣
=
1
)
=
1
2
×
1
4
1
2
×
1
8
+
1
2
×
1
4
=
2
3
\begin{aligned}p&= P(B |A)\\&= \frac{ P(AB)}{P(A)}\\&=\frac{ P(X=-1)}{ P(|X| =1 )}\\&=\frac{\frac 12 \times \frac 1 4}{\frac 12 \times \frac 1 8 +\frac 12 \times \frac 1 4}\\&=\frac 2 3 \end{aligned}
p=P(B∣A)=P(A)P(AB)=P(∣X∣=1)P(X=−1)=21×81+21×4121×41=32

- m a x P ( A ∩ B ) = m i n { P ( A ) , P ( B ) } = 0.3 maxP(A \cap B)=min\{P(A),P(B)\}=0.3 maxP(A∩B)=min{P(A),P(B)}=0.3
- m i n P ( A ∩ B ) = 0 minP(A \cap B)=0 minP(A∩B)=0
- m a x P ( A ∪ B ) = P ( A ) + P ( B ) − m i n P ( A B ) = 0.7 maxP(A \cup B)=P(A)+P(B)-minP(AB)=0.7 maxP(A∪B)=P(A)+P(B)−minP(AB)=0.7
- m i n P ( A ∪ B ) = P ( A ) + P ( B ) − m a x P ( A B ) = 0.4 minP(A \cup B)=P(A)+P(B)-maxP(AB)=0.4 minP(A∪B)=P(A)+P(B)−maxP(AB)=0.4
2 Linear Algebra
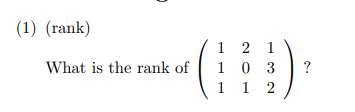
初等行变换即可,r为2
(
1
2
1
1
0
3
1
1
2
)
⟶
(
2
)
−
(
1
)
(
1
2
1
0
−
2
2
1
1
2
)
⟶
(
3
)
−
(
1
)
(
1
2
1
0
−
2
2
0
−
1
1
)
⟶
(
2
)
/
2
(
1
2
1
0
−
1
1
0
−
1
1
)
⟶
(
3
)
+
(
2
)
(
1
2
1
0
−
1
1
0
0
0
)
\left( \begin{matrix} 1 & 2 & 1 \\ 1 & 0& 3 \\ 1 & 1& 2 \end{matrix} \right) \overset{(2)-(1)} {\longrightarrow} \left( \begin{matrix} 1 & 2 & 1 \\ 0 & -2& 2 \\ 1 & 1& 2 \end{matrix} \right)\overset{(3)-(1)} {\longrightarrow} \\ \left( \begin{matrix} 1 & 2 & 1 \\ 0 & -2& 2 \\ 0 & -1& 1 \end{matrix} \right)\overset{(2)/2} {\longrightarrow}\left( \begin{matrix} 1 & 2 & 1 \\ 0 & -1& 1 \\ 0 & -1& 1 \end{matrix} \right)\overset{(3)+(2)} {\longrightarrow} \left( \begin{matrix} 1 & 2 & 1 \\ 0 & -1& 1 \\ 0 & 0& 0 \end{matrix} \right)
111201132
⟶(2)−(1)
1012−21122
⟶(3)−(1)
1002−2−1121
⟶(2)/2
1002−1−1111
⟶(3)+(2)
1002−10110
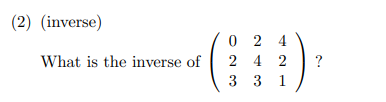
(
0
2
4
2
4
2
3
3
1
)
−
1
=
(
0
2
4
2
4
2
3
3
1
)
∗
∣
(
0
2
4
2
4
2
3
3
1
)
∣
=
(
−
2
10
−
12
4
−
12
8
−
6
6
−
4
)
−
16
\left( \begin{matrix} 0 & 2 & 4 \\ 2 & 4& 2 \\ 3 & 3& 1 \end{matrix} \right)^{-1}=\frac{\left( \begin{matrix} 0 & 2 & 4 \\ 2 & 4& 2 \\ 3 & 3& 1 \end{matrix} \right)^*}{|\left( \begin{matrix} 0 & 2 & 4 \\ 2 & 4& 2 \\ 3 & 3& 1 \end{matrix} \right)|}=\frac{\left( \begin{matrix} -2 & 10 & -12 \\ 4 & -12& 8 \\ -6 & 6& -4 \end{matrix} \right)}{-16}
023243421
−1=∣
023243421
∣
023243421
∗=−16
−24−610−126−128−4
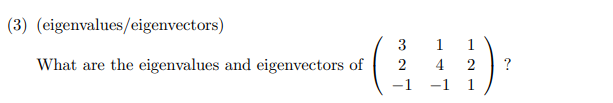
(
A
−
λ
E
)
=
(
3
−
λ
1
1
2
4
−
λ
2
−
1
−
1
1
−
λ
)
⟶
(
4
−
λ
4
−
λ
4
−
λ
0
2
−
λ
0
0
0
2
−
λ
)
=
(
4
−
λ
)
(
2
−
λ
)
2
(A-\lambda E)=\left( \begin{matrix} 3-\lambda & 1 & 1 \\ 2 & 4-\lambda & 2 \\ -1 & -1 & 1-\lambda \end{matrix} \right) \longrightarrow \left( \begin{matrix} 4-\lambda & 4-\lambda & 4-\lambda \\ 0 & 2-\lambda & 0 \\ 0 & 0 & 2-\lambda \end{matrix} \right)\\ =(4-\lambda)(2-\lambda)^2 \\
(A−λE)=
3−λ2−114−λ−1121−λ
⟶
4−λ004−λ2−λ04−λ02−λ
=(4−λ)(2−λ)2
- 当特征值为4时,有:
A − 4 E = ( − 1 1 1 2 0 2 − 1 − 1 − 3 ) ⟶ ( 1 0 1 0 1 2 0 0 0 ) A-4E=\left( \begin{matrix} -1 & 1 & 1 \\ 2 & 0 & 2 \\ -1 & -1 & -3 \end{matrix} \right)\longrightarrow \left( \begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{matrix} \right) A−4E= −12−110−112−3 ⟶ 100010120
求得 x ⃗ 1 = ( 1 2 − 1 ) \vec x_1=\left( \begin{matrix} 1 \\ 2 \\ -1 \end{matrix} \right) x1= 12−1
- 特征值为2时,同理可以求得 x ⃗ 2 = ( 1 0 − 1 ) \vec x_2=\left( \begin{matrix} 1 \\ 0 \\ -1 \end{matrix} \right) x2= 10−1 和 x ⃗ 3 = ( 1 − 1 0 ) \vec x_3=\left( \begin{matrix} 1 \\ -1 \\ 0 \end{matrix} \right) x3= 1−10

(a)
不妨认为
M
∈
R
m
×
n
,
U
∈
R
m
×
m
,
Σ
∈
R
m
×
n
,
V
∈
R
n
×
n
M\in\mathbb R^{m\times n},U\in \mathbb R^{m\times m},\Sigma\in \mathbb R^{m\times n}, V\in \mathbb R^{n\times n}
M∈Rm×n,U∈Rm×m,Σ∈Rm×n,V∈Rn×n易得
Σ
†
∈
R
n
×
m
\Sigma^{\dagger}\in \mathbb R^{n\times m}
Σ†∈Rn×m
所以有
M
M
†
M
=
U
Σ
V
T
V
Σ
†
U
T
U
Σ
V
T
=
U
(
Σ
Σ
†
)
Σ
V
T
=
U
I
m
Σ
V
T
=
U
Σ
V
T
\begin{aligned} MM^{\dagger}M &=U\Sigma V^TV\Sigma^{\dagger} U^TU\Sigma V^T\\ &=U(\Sigma\Sigma^{\dagger})\Sigma V^T\\ &=UI_m\Sigma V^T\\ &=U\Sigma V^T \end{aligned}
MM†M=UΣVTVΣ†UTUΣVT=U(ΣΣ†)ΣVT=UImΣVT=UΣVT
(b)
M
†
=
V
Σ
†
U
T
(
M
可逆,则
m
=
n
,且
Σ
†
=
Σ
−
1
)
=
V
Σ
−
1
U
T
=
(
U
Σ
V
T
)
−
1
=
M
−
1
\begin{aligned} M^{\dagger} &= V\Sigma^{\dagger} U^T(M 可逆,则m=n,且\Sigma^{\dagger}=\Sigma^{-1}) \\ &=V\Sigma^{-1} U^T \\ &=(U\Sigma V^T)^{-1}\\ &=M^{-1} \end{aligned}
M†=VΣ†UT(M可逆,则m=n,且Σ†=Σ−1)=VΣ−1UT=(UΣVT)−1=M−1

(a)
∀
x
,
x
T
Z
Z
T
x
=
(
Z
T
x
)
T
(
Z
T
x
)
≥
0
\forall x,x^T ZZ^T x= (Z^Tx)^T(Z^Tx)\ge 0
∀x,xTZZTx=(ZTx)T(ZTx)≥0,得证
(b)
- 必要性:由实对称矩阵可知,存在正交矩阵Q和对角矩阵
Λ
\Lambda
Λ使面等式成立
Q T A Q = Λ , Λ = diag { λ 1 , . . . , λ n } Q^TAQ=\Lambda,\Lambda =\text{diag} \{\lambda_1,...,\lambda_n\} QTAQ=Λ,Λ=diag{λ1,...,λn}
由已知易知, Λ \Lambda Λ>0,则必要性证明成功
- 充分性:取 x = Q e i ≠ 0 , i = 1 , . . . , n x= Qe_i\neq 0,i=1,...,n x=Qei=0,i=1,...,n,且 e i ∈ R n , ( e i ) j = 1 { i = j } e_i \in \mathbb R^n ,(e_i)_j = 1\{i=j\} ei∈Rn,(ei)j=1{i=j}
则有
x
T
Λ
x
=
e
i
T
Q
T
A
Q
e
i
=
e
i
T
Λ
e
i
=
λ
i
>
0
\begin{aligned} x^T \Lambda x &= e_i^T Q^TA Qe_i \\ &=e_i^T \Lambda e_i \\ &=\lambda_i\\ &>0 \end{aligned}
xTΛx=eiTQTAQei=eiTΛei=λi>0充分性证明成功
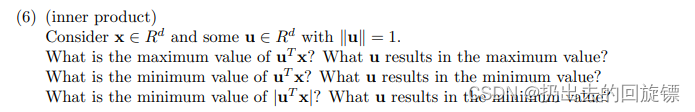
- max u t x = 1 \max u^tx=1 maxutx=1,u和x同向
- min u t x = − 1 \min u^tx=-1 minutx=−1,u和x反向
- min ∣ u t x ∣ = 0 \min |u^tx|=0 min∣utx∣=0,u和x正交
3.Calculus
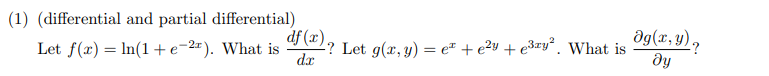
d
f
(
x
)
d
x
=
−
2
e
−
2
x
1
+
e
−
2
x
=
−
2
1
+
e
2
x
∂
g
(
x
,
y
)
∂
y
=
2
e
2
y
+
e
3
x
y
2
6
x
y
\begin{aligned} \frac {d f(x)}{dx} &= \frac {-2e^{-2x}} {1+e^{-2x}}=-\frac {2}{1+e^{2x}} \\ \frac {\partial g(x,y)}{\partial y} &= 2e^{2y}+e^{3xy^2} 6xy \end{aligned}
dxdf(x)∂y∂g(x,y)=1+e−2x−2e−2x=−1+e2x2=2e2y+e3xy26xy
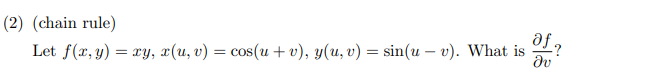
∂
f
∂
v
=
∂
f
∂
x
∂
x
∂
v
+
∂
f
∂
y
∂
y
∂
v
=
−
y
sin
(
u
+
v
)
−
x
cos
(
u
−
v
)
\begin{aligned} \frac {\partial f}{\partial v} &=\frac {\partial f}{\partial x} \frac {\partial x}{\partial v}+ \frac {\partial f}{\partial y} \frac {\partial y}{\partial v}\\ &=-y\sin(u+v)-x\cos (u-v) \end{aligned}
∂v∂f=∂x∂f∂v∂x+∂y∂f∂v∂y=−ysin(u+v)−xcos(u−v)
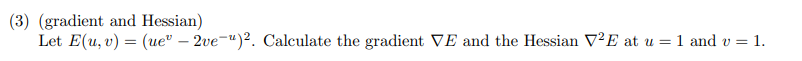
一阶偏导:
∂
E
(
u
,
v
)
∂
u
=
2
(
u
e
v
−
2
v
e
−
u
)
(
e
v
+
2
v
e
−
u
)
∂
E
(
u
,
v
)
∂
v
=
2
(
u
e
v
−
2
v
e
−
u
)
(
u
e
v
−
2
e
−
u
)
\begin{aligned} \frac{\partial E(u,v)}{\partial u} &=2(ue^v -2ve^{-u} )(e^v +2ve^{-u})\\ \frac{\partial E(u,v)}{\partial v} &=2(ue^v -2ve^{-u} )(ue^v -2e^{-u})\\ \end{aligned}
∂u∂E(u,v)∂v∂E(u,v)=2(uev−2ve−u)(ev+2ve−u)=2(uev−2ve−u)(uev−2e−u)
二阶偏导:
∂
2
E
(
u
,
v
)
∂
u
2
=
2
∂
∂
u
(
u
e
2
v
−
2
v
e
v
−
u
+
2
u
v
e
v
−
u
−
4
v
2
e
−
2
u
)
=
2
(
e
2
v
+
2
v
e
v
−
u
+
2
v
e
v
−
u
−
2
u
v
e
v
−
u
+
8
v
2
e
−
2
u
)
=
2
(
e
2
v
+
4
v
e
v
−
u
−
2
u
v
e
v
−
u
+
8
v
2
e
−
2
u
)
∂
2
E
(
u
,
v
)
∂
v
2
=
2
∂
∂
v
(
u
2
e
2
v
−
2
u
v
e
v
−
u
−
2
u
e
v
−
u
+
4
v
e
−
2
u
)
=
2
(
2
u
2
e
2
v
−
2
u
e
v
−
u
−
2
u
v
e
v
−
u
−
2
u
e
v
−
u
+
4
e
−
2
u
)
=
2
(
2
u
2
e
2
v
−
4
u
e
v
−
u
−
2
u
v
e
v
−
u
+
4
e
−
2
u
)
∂
2
E
(
u
,
v
)
∂
u
∂
v
=
2
∂
∂
v
(
u
e
2
v
−
2
v
e
v
−
u
+
2
u
v
e
v
−
u
−
4
v
2
e
−
2
u
)
=
2
(
2
u
e
2
v
−
2
e
v
−
u
−
2
v
e
v
−
u
+
2
u
e
v
−
u
+
2
u
v
e
v
−
u
−
8
v
e
−
2
u
)
\begin{aligned} \frac{\partial^2 E(u,v)}{\partial u^2} &=2\frac{\partial}{\partial u}(ue^{2v} -2v e^{v-u}+2uve^{v-u}-4v^2 e^{-2u})\\ &=2(e^{2v} +2v e^{v-u}+2ve^{v-u}-2uve^{v-u}+8v^2 e^{-2u}) \\ &=2(e^{2v} +4v e^{v-u}-2uve^{v-u}+8v^2 e^{-2u})\\ \frac{\partial^2 E(u,v)}{\partial v^2} &=2\frac{\partial}{\partial v}(u^2e^{2v} -2uv e^{v-u}-2ue^{v-u}+4ve^{-2u})\\ &=2(2u^2e^{2v} -2u e^{v-u}-2uv e^{v-u}-2ue^{v-u}+4e^{-2u})\\ &=2(2u^2e^{2v} -4u e^{v-u}-2uv e^{v-u}+4e^{-2u}) \\ \frac{\partial^2 E(u,v)}{\partial u \partial v} &=2\frac{\partial}{\partial v}(ue^{2v} -2v e^{v-u}+2uve^{v-u}-4v^2 e^{-2u})\\ &=2(2ue^{2v} -2 e^{v-u}-2ve^{v-u}+2ue^{v-u}+2uve^{v-u} -8v e^{-2u}) \\ \end{aligned}
∂u2∂2E(u,v)∂v2∂2E(u,v)∂u∂v∂2E(u,v)=2∂u∂(ue2v−2vev−u+2uvev−u−4v2e−2u)=2(e2v+2vev−u+2vev−u−2uvev−u+8v2e−2u)=2(e2v+4vev−u−2uvev−u+8v2e−2u)=2∂v∂(u2e2v−2uvev−u−2uev−u+4ve−2u)=2(2u2e2v−2uev−u−2uvev−u−2uev−u+4e−2u)=2(2u2e2v−4uev−u−2uvev−u+4e−2u)=2∂v∂(ue2v−2vev−u+2uvev−u−4v2e−2u)=2(2ue2v−2ev−u−2vev−u+2uev−u+2uvev−u−8ve−2u)
代入题目条件u、v=1有
∂
E
(
u
,
v
)
∂
u
∣
u
=
1
,
v
=
1
=
2
(
e
2
−
4
e
−
2
)
∂
E
(
u
,
v
)
∂
v
∣
u
=
1
,
v
=
1
=
2
(
e
2
+
4
e
−
2
−
4
)
∂
2
E
(
u
,
v
)
∂
u
2
∣
u
=
1
,
v
=
1
=
2
(
e
2
+
8
e
−
2
+
2
)
∂
2
E
(
u
,
v
)
∂
v
2
∣
u
=
1
,
v
=
1
=
2
(
2
e
2
+
4
e
−
2
−
6
)
∂
2
E
(
u
,
v
)
∂
u
∂
v
∣
u
=
1
,
v
=
1
=
2
(
2
e
2
−
8
e
−
2
)
\begin{aligned} \frac{\partial E(u,v)}{\partial u} \Big |_{u=1,v=1} &=2(e^2 -4e^{-2}) \\ \frac{\partial E(u,v)}{\partial v} \Big |_{u=1,v=1} &=2(e^2 +4e^{-2}-4) \\ \frac{\partial^2 E(u,v)}{\partial u^2}\Big |_{u=1,v=1}& =2(e^2+8e^{-2}+2) \\ \frac{\partial^2 E(u,v)}{\partial v^2}\Big |_{u=1,v=1}& =2(2e^2+4e^{-2}-6) \\ \frac{\partial^2 E(u,v)}{\partial u\partial v}\Big |_{u=1,v=1}& =2(2e^2 -8e^{-2}) \\ \end{aligned}
∂u∂E(u,v)
u=1,v=1∂v∂E(u,v)
u=1,v=1∂u2∂2E(u,v)
u=1,v=1∂v2∂2E(u,v)
u=1,v=1∂u∂v∂2E(u,v)
u=1,v=1=2(e2−4e−2)=2(e2+4e−2−4)=2(e2+8e−2+2)=2(2e2+4e−2−6)=2(2e2−8e−2)
最后结果为:
∇
E
=
(
2
(
e
2
−
4
e
−
2
)
2
(
e
2
+
4
e
−
2
−
4
)
)
,
∇
2
E
=
(
2
(
e
2
+
8
e
−
2
+
2
)
2
(
2
e
2
−
8
e
−
2
)
2
(
2
e
2
−
8
e
−
2
)
2
(
2
e
2
+
4
e
−
2
−
6
)
)
\begin{aligned} \nabla E= \left( \begin{matrix} 2(e^2 -4e^{-2}) \\ 2(e^2 +4e^{-2}-4) \end{matrix} \right) , \nabla^2 E = \left( \begin{matrix} 2(e^2+8e^{-2}+2) & 2(2e^2 -8e^{-2}) \\ 2(2e^2 -8e^{-2}) & 2(2e^2+4e^{-2}-6) \end{matrix} \right) \end{aligned}
∇E=(2(e2−4e−2)2(e2+4e−2−4)),∇2E=(2(e2+8e−2+2)2(2e2−8e−2)2(2e2−8e−2)2(2e2+4e−2−6))

E
(
u
,
v
)
≈
E
(
1
,
1
)
+
∇
E
T
(
u
−
1
v
−
1
)
+
1
2
!
(
u
−
1
v
−
1
)
∇
2
E
(
u
−
1
v
−
1
)
=
(
e
−
2
e
−
1
)
2
+
2
(
e
2
−
4
e
−
2
)
(
u
−
1
)
+
2
(
e
2
+
4
e
−
2
−
4
)
(
v
−
1
)
+
(
e
2
+
8
e
−
2
+
2
)
(
u
−
1
)
2
+
(
2
e
2
+
4
e
−
2
−
6
)
(
v
−
1
)
2
+
2
(
2
e
2
−
8
e
−
2
)
(
u
−
1
)
(
v
−
1
)
\begin{aligned} E(u,v) &\approx E(1, 1)+ \nabla E^T \left( \begin{matrix} u- 1 \\ v- 1 \end{matrix} \right) + \frac 1 {2!} \left( \begin{matrix} u- 1 & v- 1 \end{matrix} \right) \nabla^2 E \left( \begin{matrix} u- 1 \\ v- 1 \end{matrix} \right) \\ &=(e-2e^{-1})^2 + 2(e^2 -4e^{-2}) (u-1)+ 2(e^2 +4e^{-2}-4)(v-1)\\ &+(e^2+8e^{-2}+2) (u-1)^2 + (2e^2+4e^{-2}-6)(v-1)^2+2(2e^2 -8e^{-2})(u-1)(v-1) \end{aligned}
E(u,v)≈E(1,1)+∇ET(u−1v−1)+2!1(u−1v−1)∇2E(u−1v−1)=(e−2e−1)2+2(e2−4e−2)(u−1)+2(e2+4e−2−4)(v−1)+(e2+8e−2+2)(u−1)2+(2e2+4e−2−6)(v−1)2+2(2e2−8e−2)(u−1)(v−1)
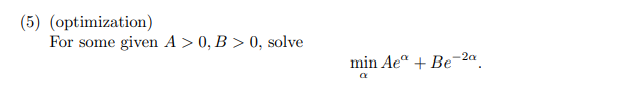
A
e
α
+
B
e
−
2
α
=
A
2
e
α
+
A
2
e
α
+
B
e
−
2
α
≥
3
A
2
e
α
×
A
2
e
α
×
B
e
−
2
α
3
=
3
A
2
B
4
3
\begin{aligned} &Ae^{\alpha} +Be^{-2\alpha}\\ &=\frac A 2 e^{\alpha}+\frac A 2 e^{\alpha} +Be^{-2\alpha}\\ &\ge 3 \sqrt[3] {\frac A 2 e^{\alpha}\times\frac A 2 e^{\alpha} \times Be^{-2\alpha}} \\ &=3\sqrt[3]{\frac {A^2B} 4} \end{aligned}
Aeα+Be−2α=2Aeα+2Aeα+Be−2α≥332Aeα×2Aeα×Be−2α=334A2B当且仅当
A
2
e
α
=
A
2
e
α
=
B
e
−
2
α
α
=
1
3
ln
2
B
A
\begin{aligned}&\frac A 2 e^{\alpha}=\frac A 2 e^{\alpha} =Be^{-2\alpha}\\ &\alpha =\frac 1 3 \ln \frac {2B} A\end{aligned}
2Aeα=2Aeα=Be−2αα=31lnA2B
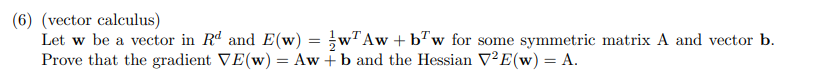
原式展开有:
E
(
w
)
=
1
2
∑
i
=
1
d
∑
j
=
1
d
w
i
A
i
j
w
j
+
∑
i
=
1
d
w
i
b
i
\begin{aligned} E(w) & =\frac 1 2 \sum_{i=1}^d \sum_{j=1}^d w_{i}A_{ij}w_j + \sum_{i=1}^d w_i b_i \end{aligned}
E(w)=21i=1∑dj=1∑dwiAijwj+i=1∑dwibi
由于A是对称矩阵:
∂
E
(
w
)
∂
w
k
=
1
2
∑
j
=
1
d
A
k
j
w
j
+
1
2
∑
i
=
1
d
w
i
A
i
k
+
b
k
=
∑
j
=
1
d
A
k
j
w
j
+
b
k
∂
2
E
(
w
)
∂
w
l
∂
w
k
=
∂
∂
w
l
(
∑
j
=
1
d
A
k
j
w
j
+
b
k
)
=
A
k
l
\begin{aligned} \frac{\partial E(w)}{\partial w_k} &=\frac 1 2 \sum_{j=1}^d A_{kj}w_j+\frac 1 2 \sum_{i=1}^d w_{i}A_{ik} + b_k \\ &=\sum_{j=1}^d A_{kj}w_j +b_k \\ \frac{\partial^2 E(w)}{\partial w_l\partial w_k} &= \frac{\partial}{\partial w_l} \Big(\sum_{j=1}^d A_{kj}w_j +b_k \Big)\\ &= A_{kl} \\ \end{aligned}
∂wk∂E(w)∂wl∂wk∂2E(w)=21j=1∑dAkjwj+21i=1∑dwiAik+bk=j=1∑dAkjwj+bk=∂wl∂(j=1∑dAkjwj+bk)=Akl
合成为矩阵形式有:
∇
E
(
w
)
=
A
w
+
b
∇
E
2
(
w
)
=
A
\begin{aligned} \nabla E(w)& =Aw+b\\ \nabla E^2(w)& =A \end{aligned}
∇E(w)∇E2(w)=Aw+b=A
一览图




![[CCS 2022] 皇帝没有衣服:用于网络安全的AI/ML](https://img-blog.csdnimg.cn/img_convert/8c527794a3a202e9169432129ca7542c.png)