多传感器融合定位十四-基于图优化的定位方法
- 1. 基于图优化的定位简介
- 1.1 核心思路
- 1.2 定位流程
- 2. 边缘化原理及应用
- 2.1 边缘化原理
- 2.2 从滤波角度理解边缘化
- 3. 基于kitti的实现原理
- 3.1 基于地图定位的滑动窗口模型
- 3.2 边缘化过程
- 4. lio-mapping 介绍
- 4.1 核心思想
- 4.2 具体流程
- 4.2.1 各类因子
- 4.2.2 滑窗模型
- 4.2.3 边缘化
- 4.2.4 添加新帧
Reference:
- 深蓝学院-多传感器融合
- 多传感器融合定位理论基础
文章跳转：
- 多传感器融合定位一-3D激光里程计其一：ICP
- 多传感器融合定位二-3D激光里程计其二：NDT
- 多传感器融合定位三-3D激光里程计其三：点云畸变补偿
- 多传感器融合定位四-3D激光里程计其四：点云线面特征提取
- 多传感器融合定位五-点云地图构建及定位
- 多传感器融合定位六-惯性导航原理及误差分析
- 多传感器融合定位七-惯性导航解算及误差分析其一
- 多传感器融合定位八-惯性导航解算及误差分析其二
- 多传感器融合定位九-基于滤波的融合方法Ⅰ其一
- 多传感器融合定位十-基于滤波的融合方法Ⅰ其二
- 多传感器融合定位十一-基于滤波的融合方法Ⅱ
- 多传感器融合定位十二-基于图优化的建图方法其一
- 多传感器融合定位十三-基于图优化的建图方法其二
- 多传感器融合定位十四-基于图优化的定位方法
- 多传感器融合定位十五-多传感器时空标定(综述)
1. 基于图优化的定位简介
1.1 核心思路
核心思路是把融合方法从滤波换成图优化，其元素不再是简单的惯性解算，而是预积分。
一个暴力的模型可以设计为：
缺陷：随着时间的进行，图模型会越来越大，导致无法达到实时性。
解决方法：不断删除旧的帧，只优化最新的几帧，即维持一个滑动窗口。
模型如下：
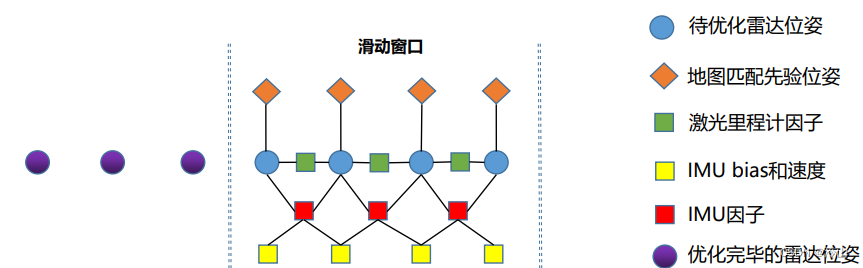
问题：直接从模型中删除，等于损失了信息。
解法：通过模型把旧帧的约束传递下来，即边缘化(后面讲具体细节)。
1.2 定位流程
整个流程：不断往滑窗里添加新信息，并边缘化旧信息。
需要注意的是：
- 正常行驶时，不必像建图那样，提取稀疏的关键帧；
- 停车时，需要按一定策略提取关键帧，但删除的是次新帧，因此不需要边缘化。
2. 边缘化原理及应用
2.1 边缘化原理
优化问题具有如下通用形式:
H
X
=
b
H X=b
HX=b并可拆解成如下形式:
[
H
m
m
H
m
r
H
r
m
H
r
r
]
[
X
m
X
r
]
=
[
b
m
b
r
]
\left[\begin{array}{cc} H_{m m} & H_{m r} \\ H_{r m} & H_{r r} \end{array}\right]\left[\begin{array}{c} X_m \\ X_r \end{array}\right]=\left[\begin{array}{l} b_m \\ b_r \end{array}\right]
[HmmHrmHmrHrr][XmXr]=[bmbr]拆解的目的是通过一系列操作，把
X
m
X_m
Xm 从状态量 里删除掉，并把它的约束保留下来。
在滑窗模式里，这个
X
m
X_m
Xm 即为要边缘化掉的量。
回顾舒尔补：
给定矩阵
M
=
[
A
B
C
D
]
M=\left[\begin{array}{ll} \mathrm{A} & \mathrm{B} \\ \mathrm{C} & \mathrm{D} \end{array}\right]
M=[ACBD]它可以通过如下变换，变成上三角矩阵，即
[
I
0
−
C
A
−
1
I
]
[
A
B
C
D
]
=
[
A
B
0
Δ
A
]
\left[\begin{array}{cc} \mathrm{I} & 0 \\ -\mathrm{CA}^{-1} & \mathrm{I} \end{array}\right]\left[\begin{array}{cc} \mathrm{A} & \mathrm{B} \\ \mathrm{C} & \mathrm{D} \end{array}\right]=\left[\begin{array}{cc} \mathrm{A} & \mathrm{B} \\ 0 & \Delta \mathrm{A} \end{array}\right]
[I−CA−10I][ACBD]=[A0BΔA]其中，
Δ
A
=
D
−
C
A
−
1
B
\Delta \mathrm{A}=\mathrm{D}-\mathrm{CA}^{-1} \mathrm{~B}
ΔA=D−CA−1 B 称为
A
\mathrm{A}
A 关于
M
\mathrm{M}
M 的舒尔补。
拆解后的优化问题，可通过舒尔补对矩阵三角化， 即
[
I
0
−
H
r
m
H
m
m
−
1
I
]
[
H
m
m
H
m
r
H
r
m
H
r
r
]
[
X
m
X
r
]
=
[
I
0
−
H
r
m
H
m
m
−
1
I
]
[
b
m
b
r
]
\begin{aligned} & {\left[\begin{array}{cc} I & 0 \\ -H_{r m} H_{m m}^{-1} & I \end{array}\right]\left[\begin{array}{cc} H_{m m} & H_{m r} \\ H_{r m} & H_{r r} \end{array}\right]\left[\begin{array}{c} X_m \\ X_r \end{array}\right] } \\ = & {\left[\begin{array}{cc} I & 0 \\ -H_{r m} H_{m m}^{-1} & I \end{array}\right]\left[\begin{array}{l} b_m \\ b_r \end{array}\right] } \end{aligned}
=[I−HrmHmm−10I][HmmHrmHmrHrr][XmXr][I−HrmHmm−10I][bmbr]
进一步化简得，
[
H
m
m
H
m
r
0
H
r
r
−
H
r
m
H
m
m
−
1
H
m
r
]
[
X
m
X
r
]
=
[
b
m
b
r
−
H
r
m
H
m
m
−
1
b
m
]
\begin{aligned} & {\left[\begin{array}{cc} H_{m m} & H_{m r} \\ 0 & H_{r r}-H_{r m} H_{m m}^{-1} H_{m r} \end{array}\right]\left[\begin{array}{c} X_m \\ X_r \end{array}\right] } \\ = & {\left[\begin{array}{c} b_m \\ b_r-H_{r m} H_{m m}^{-1} b_m \end{array}\right] } \end{aligned}
=[Hmm0HmrHrr−HrmHmm−1Hmr][XmXr][bmbr−HrmHmm−1bm]此时，可以利用等式第2行直接得到:
(
H
r
r
−
H
r
m
H
m
m
−
1
H
m
r
)
X
r
=
b
r
−
H
r
m
H
m
m
−
1
b
m
\left(H_{r r}-H_{r m} H_{m m}^{-1} H_{m r}\right) X_r=b_r-H_{r m} H_{m m}^{-1} b_m
(Hrr−HrmHmm−1Hmr)Xr=br−HrmHmm−1bm
其含义为：此时可以不依赖
X
m
X_m
Xm 求解出
X
r
X_r
Xr，若我们只关心
X
r
X_r
Xr 的值，则可以把
X
m
X_m
Xm 从模型里删除。
2.2 从滤波角度理解边缘化
kalman滤波是此前已经熟悉的，从边缘化的 角度重新看一遍滤波器的推导，更有利于深入 理解。
运动模型与观测模型分别为:
x
k
=
A
k
−
1
x
k
−
1
+
v
k
+
w
k
y
k
=
C
k
x
k
+
n
k
\begin{aligned} & \mathbf{x}_k=\mathbf{A}_{k-1} \mathbf{x}_{k-1}+\mathbf{v}_k+\mathbf{w}_k \\ & \mathbf{y}_k=\mathbf{C}_k \mathbf{x}_k+\mathbf{n}_k \end{aligned}
xk=Ak−1xk−1+vk+wkyk=Ckxk+nk
其中
k
=
1
…
K
k=1 \ldots K
k=1…K状态量的求解，可以等效为如下模型
x
^
=
arg
min
x
J
(
x
)
\hat{\mathbf{x}}=\arg \min _{\mathbf{x}} J(\mathbf{x})
x^=argxminJ(x)
其中
J
(
x
)
=
∑
k
=
0
K
(
J
v
,
k
(
x
)
+
J
y
,
k
(
x
)
)
J
v
,
k
(
x
)
=
{
1
2
(
x
0
−
x
ˇ
0
)
T
P
ˇ
0
−
1
(
x
0
−
x
ˇ
0
)
,
k
=
0
1
2
(
x
k
−
A
k
−
1
x
k
−
1
−
v
k
)
T
×
Q
k
−
1
(
x
k
−
A
k
−
1
x
k
−
1
−
v
k
)
,
k
=
1
…
K
J
y
,
k
(
x
)
=
1
2
(
y
k
−
C
k
x
k
)
T
R
k
−
1
(
y
k
−
C
k
x
k
)
,
k
=
0
…
K
\begin{aligned} & J(\mathbf{x})=\sum_{k=0}^K\left(J_{v, k}(\mathbf{x})+J_{y, k}(\mathbf{x})\right) \\ & J_{v, k}(\mathbf{x})=\left\{\begin{array}{c} \frac{1}{2}\left(\mathbf{x}_0-\check{\mathbf{x}}_0\right)^T \check{\mathbf{P}}_0^{-1}\left(\mathbf{x}_0-\check{\mathbf{x}}_0\right), k=0 \\ \frac{1}{2}\left(\mathbf{x}_k-\mathbf{A}_{k-1} \mathbf{x}_{k-1}-\mathbf{v}_k\right)^T \\ \times \mathbf{Q}_k^{-1}\left(\mathbf{x}_k-\mathbf{A}_{k-1} \mathbf{x}_{k-1}-\mathbf{v}_k\right), k=1 \ldots K \end{array}\right. \\ & J_{y, k}(\mathbf{x})=\frac{1}{2}\left(\mathbf{y}_k-\mathbf{C}_k \mathbf{x}_k\right)^T \mathbf{R}_k^{-1}\left(\mathbf{y}_k-\mathbf{C}_k \mathbf{x}_k\right), \quad k=0 \ldots K \end{aligned}
J(x)=k=0∑K(Jv,k(x)+Jy,k(x))Jv,k(x)=⎩
⎨
⎧21(x0−xˇ0)TPˇ0−1(x0−xˇ0),k=021(xk−Ak−1xk−1−vk)T×Qk−1(xk−Ak−1xk−1−vk),k=1…KJy,k(x)=21(yk−Ckxk)TRk−1(yk−Ckxk),k=0…K将上述模型整理为更简洁的形式，令
z
=
[
x
ˇ
0
v
1
⋮
v
K
y
0
y
1
⋮
y
K
]
,
x
=
[
x
0
⋮
x
K
]
\mathbf{z}=\left[\begin{array}{c} \check{\mathbf{x}}_0 \\ \mathbf{v}_1 \\ \vdots \\ \mathbf{v}_K \\ \hline \mathbf{y}_0 \\ \mathbf{y}_1 \\ \vdots \\ \mathbf{y}_K \end{array}\right], \quad \mathbf{x}=\left[\begin{array}{c} \mathbf{x}_0 \\ \vdots \\ \mathbf{x}_K \end{array}\right]
z=
xˇ0v1⋮vKy0y1⋮yK
,x=
x0⋮xK
H
=
[
1
−
A
0
1
⋱
⋱
−
A
K
−
1
1
C
0
C
1
⋱
C
K
]
W
=
[
P
ˇ
0
Q
1
⋱
Q
K
R
0
R
1
R
K
]
\begin{aligned} & \mathbf{H}=\left[\begin{array}{cccc} \mathbf{1} & & & \\ -\mathbf{A}_0 & \mathbf{1} & & \\ & \ddots & \ddots & \\ & & -\mathbf{A}_{K-1} & \mathbf{1} \\ \hline \mathbf{C}_0 & \mathbf{C}_1 & & \\ & & \ddots & \\ & & & \mathbf{C}_K \end{array}\right] \\ & \mathbf{W}=\left[\begin{array}{llll|lll} \check{\mathbf{P}}_0 & & & & & & \\ & \mathbf{Q}_1 & & & & & \\ & & \ddots & & & \\ & & & \mathbf{Q}_K & & & \\ \hline & & & & \mathbf{R}_0 & & \\ & & & & & \mathbf{R}_1 & \\ & & & & & \mathbf{R}_K \end{array}\right] \\ & \end{aligned}
H=
1−A0C01⋱C1⋱−AK−1⋱1CK
W=
Pˇ0Q1⋱QKR0R1RK
此时，目标函数可以重新表示为
J
(
x
)
=
1
2
(
z
−
H
x
)
T
W
−
1
(
z
−
H
x
)
J(\mathbf{x})=\frac{1}{2}(\mathbf{z}-\mathbf{H x})^T \mathbf{W}^{-1}(\mathbf{z}-\mathbf{H x})
J(x)=21(z−Hx)TW−1(z−Hx)求解其最小值，即令其一阶导为零
∂
J
(
x
)
∂
x
T
∣
x
^
=
−
H
T
W
−
1
(
z
−
H
x
^
)
=
0
\left.\frac{\partial J(\mathbf{x})}{\partial \mathbf{x}^T}\right|_{\hat{\mathbf{x}}}=-\mathbf{H}^T \mathbf{W}^{-1}(\mathbf{z}-\mathbf{H} \hat{\mathbf{x}})=\mathbf{0}
∂xT∂J(x)
x^=−HTW−1(z−Hx^)=0即
(
H
T
W
−
1
H
)
x
^
=
H
T
W
−
1
z
\left(\mathbf{H}^T \mathbf{W}^{-1} \mathbf{H}\right) \hat{\mathbf{x}}=\mathbf{H}^T \mathbf{W}^{-1} \mathbf{z}
(HTW−1H)x^=HTW−1z然而，这是批量求解模型，当只关心当前时 刻(k时刻)状态时，应改为滤波模型。
假设上一时刻后验为
{
x
^
k
−
1
,
P
^
k
−
1
}
\left\{\hat{\mathbf{x}}_{k-1}, \hat{\mathbf{P}}_{k-1}\right\}
{x^k−1,P^k−1}
目标是得到当前时刻后验
{
x
^
k
−
1
,
P
^
k
−
1
,
v
k
,
y
k
}
↦
{
x
^
k
,
P
^
k
}
\left\{\hat{\mathbf{x}}_{k-1}, \hat{\mathbf{P}}_{k-1}, \mathbf{v}_k, \mathbf{y}_k\right\} \mapsto\left\{\hat{\mathbf{x}}_k, \hat{\mathbf{P}}_k\right\}
{x^k−1,P^k−1,vk,yk}↦{x^k,P^k}由于马尔可夫性，仅与前一时刻有关，因此令
z
k
=
[
x
^
k
−
1
v
k
y
k
]
H
k
=
[
1
−
A
k
−
1
1
C
k
]
W
k
=
[
P
^
k
−
1
Q
k
R
k
]
\begin{aligned} \mathbf{z}_k & =\left[\begin{array}{c} \hat{\mathbf{x}}_{k-1} \\ \mathbf{v}_k \\ \mathbf{y}_k \end{array}\right] \\ \mathbf{H}_k & =\left[\begin{array}{ccc} \mathbf{1} & \\ -\mathbf{A}_{k-1} & 1 \\ & \mathbf{C}_k \end{array}\right] \\ \mathbf{W}_k & =\left[\begin{array}{ccc} \hat{\mathbf{P}}_{k-1} & \\ & \mathbf{Q}_k & \\ & & \mathbf{R}_k \end{array}\right] \end{aligned}
zkHkWk=
x^k−1vkyk
=
1−Ak−11Ck
=
P^k−1QkRk
则模型的解为
(
H
k
T
W
k
−
1
H
k
)
x
^
=
H
k
T
W
k
−
1
z
k
\left(\mathbf{H}_k^T \mathbf{W}_k^{-1} \mathbf{H}_k\right) \hat{\mathbf{x}}=\mathbf{H}_k^T \mathbf{W}_k^{-1} \mathbf{z}_k
(HkTWk−1Hk)x^=HkTWk−1zk
其中
x
^
=
[
x
^
k
−
1
′
x
^
k
]
\hat{\mathbf{x}}=\left[\begin{array}{c} \hat{\mathbf{x}}_{k-1}^{\prime} \\ \hat{\mathbf{x}}_k \end{array}\right]
x^=[x^k−1′x^k]
x
^
k
−
1
\hat{\mathbf{x}}_{k-1}
x^k−1 和
x
^
k
−
1
′
\hat{\mathbf{x}}_{k-1}^{\prime}
x^k−1′ 有本质区别，下图可以明确展示
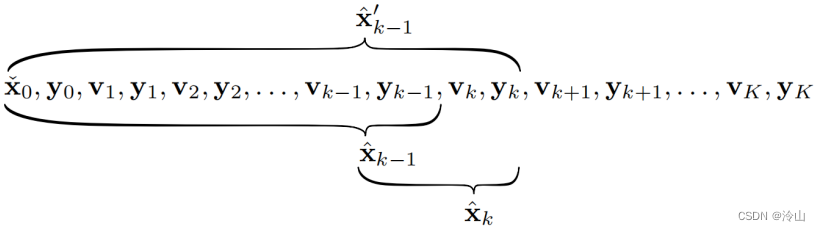
在此基础上，求解模型可以展开为
[
P
^
k
−
1
−
1
+
A
k
−
1
T
Q
k
−
1
A
k
−
1
−
A
k
−
1
T
Q
k
−
1
−
Q
k
−
1
A
k
−
1
Q
k
−
1
+
C
k
T
R
k
−
1
C
k
]
[
x
^
k
−
1
′
x
^
k
]
=
[
P
^
k
−
1
−
1
x
^
k
−
1
−
A
k
−
1
T
Q
k
−
1
v
k
Q
k
−
1
v
k
+
C
k
T
R
k
−
1
y
k
]
\left[\begin{array}{cc} \hat{\mathbf{P}}_{k-1}^{-1}+\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \mathbf{A}_{k-1} & -\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \\ -\mathbf{Q}_k^{-1} \mathbf{A}_{k-1} & \mathbf{Q}_k^{-1}+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{C}_k \end{array}\right]\left[\begin{array}{c} \hat{\mathbf{x}}_{k-1}^{\prime} \\ \hat{\mathbf{x}}_k \end{array}\right]=\left[\begin{array}{c} \hat{\mathbf{P}}_{k-1}^{-1} \hat{\mathbf{x}}_{k-1}-\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \mathbf{v}_k \\ \mathbf{Q}_k^{-1} \mathbf{v}_k+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{y}_k \end{array}\right]
[P^k−1−1+Ak−1TQk−1Ak−1−Qk−1Ak−1−Ak−1TQk−1Qk−1+CkTRk−1Ck][x^k−1′x^k]=[P^k−1−1x^k−1−Ak−1TQk−1vkQk−1vk+CkTRk−1yk]利用舒尔补，等式两边左乘如下矩阵，便可以直接求解出
x
^
k
\hat{\mathbf{x}}_k
x^k ，且不需求解
x
^
k
−
1
′
\hat{\mathbf{x}}_{k-1}^{\prime}
x^k−1′
[
1
0
Q
k
−
1
A
k
−
1
(
P
^
k
−
1
−
1
+
A
k
−
1
T
Q
k
−
1
A
k
−
1
)
−
1
1
]
\left[\begin{array}{cc} \mathbf{1} & \mathbf{0} \\ \mathbf{Q}_k^{-1} \mathbf{A}_{k-1}\left(\hat{\mathbf{P}}_{k-1}^{-1}+\mathbf{A}_{k-1}^T \mathbf{Q}_k^{-1} \mathbf{A}_{k-1}\right)^{-1} & \mathbf{1} \end{array}\right]
[1Qk−1Ak−1(P^k−1−1+Ak−1TQk−1Ak−1)−101]可得:
P
^
k
−
1
x
^
k
=
P
ˇ
k
−
1
(
A
k
−
1
x
^
k
−
1
+
v
k
)
+
C
k
T
R
k
−
1
y
k
\hat{\mathbf{P}}_k^{-1} \hat{\mathbf{x}}_k=\check{\mathbf{P}}_k^{-1}\left(\mathbf{A}_{k-1} \hat{\mathbf{x}}_{k-1}+\mathbf{v}_k\right)+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{y}_k
P^k−1x^k=Pˇk−1(Ak−1x^k−1+vk)+CkTRk−1yk其中
P
ˇ
k
=
Q
k
+
A
k
−
1
P
^
k
−
1
A
k
−
1
T
P
^
k
=
(
P
ˇ
k
−
1
+
C
k
T
R
k
−
1
C
k
)
−
1
\begin{aligned} & \check{\mathbf{P}}_k=\mathbf{Q}_k+\mathbf{A}_{k-1} \hat{\mathbf{P}}_{k-1} \mathbf{A}_{k-1}^T \\ & \hat{\mathbf{P}}_k=\left(\check{\mathbf{P}}_k^{-1}+\mathbf{C}_k^T \mathbf{R}_k^{-1} \mathbf{C}_k\right)^{-1} \end{aligned}
Pˇk=Qk+Ak−1P^k−1Ak−1TP^k=(Pˇk−1+CkTRk−1Ck)−1以上过程，核心即为边缘化，因此滤波(IEKF)可以看做长度为1的滑动窗口。
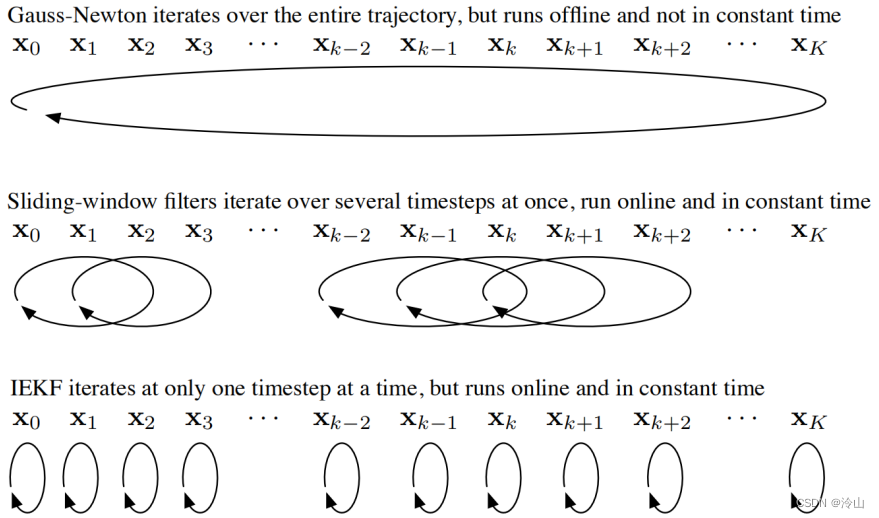
3. 基于kitti的实现原理
3.1 基于地图定位的滑动窗口模型
-
窗口优化模型构成
在图优化模型中，优化模型也可写成如下形式：
J ⊤ Σ J δ x = − J ⊤ Σ r \mathbf{J}^{\top} \boldsymbol{\Sigma} \mathbf{J} \delta \boldsymbol{x}=-\mathbf{J}^{\top} \boldsymbol{\Sigma} \mathbf{r} J⊤ΣJδx=−J⊤Σr其中
r r r 是残差；
J J J 是残差关于状态量的雅可比；
∑ \sum ∑ 是信息矩阵。
在kitti工程中，基于地图定位的滑动窗口，其残差包括:- 地图匹配位姿和优化变量的残差
- 激光里程计相对位姿和优化变量的残差
- IMU预积分和优化变量的残差
- 边缘化形成的先验因子对应的残差
此处先介绍前3项，第4项待边缘化后介绍。
-
地图匹配位姿和优化变量的残差
该残差对应的因子为地图先验因子。
一个因子仅约束一个位姿，其模型如下：
残差关于优化变量的雅可比，可视化如下：
因此，对应的Hessian矩阵的可视化为：
-
激光里程计相对位姿和优化变量的残差
该残差对应的因子为激光里程计因子。
一个因子约束两个位姿，其模型如下：
残差关于优化变量的雅可比，可视化如下：
因此，对应的Hessian矩阵可视化为：
-
IMU预积分和优化变量的残差
该残差对应的因子为IMU因子。
一个因子约束两个位姿，并约束两个时刻 IMU
的速度与 bias。
残差关于优化变量的雅可比，可视化如下：
因此，对应的Hessian矩阵可视化为：
-
完整模型
完整Hessian矩阵，即为以上各因子对应矩阵的累加。
上述过程用公式可表示为:
J ⊤ Σ J ⏟ H δ x = − J ⊤ Σ r ⏟ b \underbrace{\mathbf{J}^{\top} \boldsymbol{\Sigma} \mathbf{J}}_{\mathbf{H}} \delta \boldsymbol{x}=\underbrace{-\mathbf{J}^{\top} \boldsymbol{\Sigma} \boldsymbol{r}}_{\text {b }} H J⊤ΣJδx=b −J⊤Σr其中
r = [ r Y 0 r Y 1 r Y 2 r L 0 r L 1 r M 0 r M 1 ] \boldsymbol{r}=\left[\begin{array}{l} \boldsymbol{r}_{Y 0} \\ \boldsymbol{r}_{Y 1} \\ \boldsymbol{r}_{Y 2} \\ \boldsymbol{r}_{L 0} \\ \boldsymbol{r}_{L 1} \\ \boldsymbol{r}_{M 0} \\ \boldsymbol{r}_{M 1} \end{array}\right] r= rY0rY1rY2rL0rL1rM0rM1
J = ∂ r ∂ δ x = [ ∂ r 0 ∂ δ 0 ∂ r 1 ∂ δ x ∂ r 2 ∂ δ x ∂ r L 0 ∂ δ x ∂ r L 1 ∂ δ x ∂ r M 0 ∂ δ x ∂ r M 1 ∂ δ x ] = [ J 1 J 2 J 3 J 4 J 5 J 6 J 7 ] J ⊤ = [ J 1 ⊤ J 2 ⊤ J 3 ⊤ J 4 ⊤ J 5 ⊤ J 6 ⊤ J 7 ⊤ ] \begin{aligned} & \mathbf{J}=\frac{\partial \mathbf{r}}{\partial \delta x}=\left[\begin{array}{c} \frac{\partial \mathbf{r}_0}{\partial \delta_0} \\ \frac{\partial \mathbf{r}_1}{\partial \delta x} \\ \frac{\partial \mathbf{r}_2}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{L 0}}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{L 1}}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{M 0}}{\partial \delta x} \\ \frac{\partial \mathbf{r}_{M 1}}{\partial \delta x} \end{array}\right]=\left[\begin{array}{l} \mathbf{J}_1 \\ \mathbf{J}_2 \\ \mathbf{J}_3 \\ \mathbf{J}_4 \\ \mathbf{J}_5 \\ \mathbf{J}_6 \\ \mathbf{J}_7 \end{array}\right] \\ & \mathbf{J}^{\top}=\left[\begin{array}{lllllll} \mathbf{J}_1^{\top} & \mathbf{J}_2^{\top} & \mathbf{J}_3^{\top} & \mathbf{J}_4^{\top} & \mathbf{J}_5^{\top} & \mathbf{J}_6^{\top} & \mathbf{J}_7^{\top} \end{array}\right] \\ & \end{aligned} J=∂δx∂r= ∂δ0∂r0∂δx∂r1∂δx∂r2∂δx∂rL0∂δx∂rL1∂δx∂rM0∂δx∂rM1 = J1J2J3J4J5J6J7 J⊤=[J1⊤J2⊤J3⊤J4⊤J5⊤J6⊤J7⊤]矩阵乘法写成累加形式为:
∑ i = 1 7 J i ⊤ Σ i J i δ x = − ∑ i = 1 7 J i ⊤ Σ i r i \sum_{i=1}^7 \mathbf{J}_i^{\top} \boldsymbol{\Sigma}_i \mathbf{J}_i \delta \boldsymbol{x}=-\sum_{i=1}^7 \mathbf{J}_i^{\top} \boldsymbol{\Sigma}_i \mathbf{r}_i i=1∑7Ji⊤ΣiJiδx=−i=1∑7Ji⊤Σiri此累加过程，即对应前面可视化时各矩阵叠加。
3.2 边缘化过程
-
移除老的帧
假设窗口长度为3，在加入新的帧之前，需要先边缘化掉老的帧，即下图方框中的变量。
用前述公式，可以表示为
( H r r − H r m H m m − 1 H m r ) δ x r = b r − H r m H m m − 1 b m \left(H_{r r}-H_{r m} H_{m m}^{-1} H_{m r}\right) \delta x_r=b_r-H_{r m} H_{m m}^{-1} b_m (Hrr−HrmHmm−1Hmr)δxr=br−HrmHmm−1bm但是在实际代码中，会把它拆成两步实现。第一步：使用和要边缘化掉的量无关的因子，构建剩余变量对应的Hessian矩阵。
上标 a a a 代表是第一步中的变量，包含Hessian矩阵的完整表达式为
H r r a δ x r = b r a H_{r r}^a \delta x_r=b_r^a Hrraδxr=bra第二步：挑出和要边缘化掉的量相关的因子，构建待边缘化的Hessian矩阵，并使用舒尔补做边缘化。
上标 b b b 代表是第二步中的变量，包含Hessian矩阵的完整表达式为
[ H r r b − H r m b ( H m m b ) − 1 H m r b ] δ x r = b r b − H r m b ( H m m b ) − 1 b m b \left[H_{r r}^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} H_{m r}^b\right] \delta x_r=b_r^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} b_m^b [Hrrb−Hrmb(Hmmb)−1Hmrb]δxr=brb−Hrmb(Hmmb)−1bmb这一步形成的约束(上式)就叫先验因子，它包含了边缘化掉的量对剩余变量的约束关系。
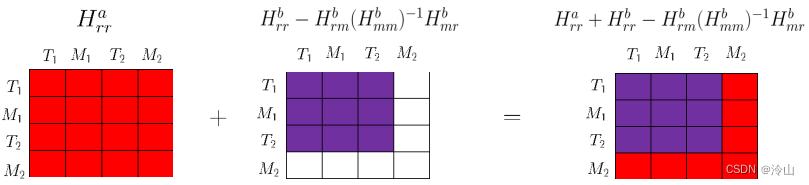
最终使用的是两步的叠加，Hessian矩阵叠加的可视化如下：
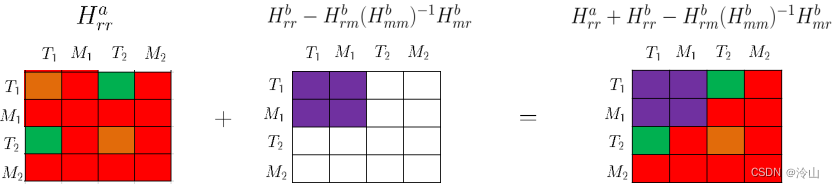
对应的完整公式为
H r r δ x r = b r H_{r r} \delta x_r=b_r Hrrδxr=br其中
H r r = H r r a + H r r b − H r m b ( H m m b ) − 1 H m r b b r = b r a + b r b − H r m b ( H m m b ) − 1 b m b \begin{gathered} H_{r r}=H_{r r}^a+H_{r r}^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} H_{m r}^b \\ b_r=b_r^a+b_r^b-H_{r m}^b\left(H_{m m}^b\right)^{-1} b_m^b \end{gathered} Hrr=Hrra+Hrrb−Hrmb(Hmmb)−1Hmrbbr=bra+brb−Hrmb(Hmmb)−1bmb边缘化之后，模型如下：
注意：边缘化先验因子只有在第一次边缘化之前是不存在的，完成第一次边缘化之后就一直存在，并且随着后续新的边缘化进行，其内容不断更新。 -
添加新的帧
添加新的帧之后，模型如下：
此处直接给出新的Hessian矩阵可视化结果：
此后，随着定位过程的进行，便不断循环“边缘化老帧->添加新帧”的过程，从而维持窗口长度不变。
该过程的代码实现可参考后面lio-mapping的实现，理解后者便很容易实现前者。
4. lio-mapping 介绍
4.1 核心思想
基于滑动窗口方法，把雷达线/面特征、IMU预积分等的约束放在一起进行优化。
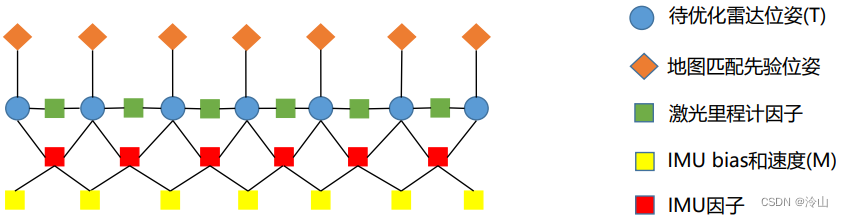
- 𝑜 𝑜 o 到 𝑖 𝑖 i 是滑窗；
- 只有 𝑝 𝑝 p 到 𝑖 𝑖 i 的位姿在滑窗中优化；
- 𝑜 𝑜 o 到 𝑝 𝑝 p 是为了构建局部地图，防止地图过于稀疏；
- 局部地图都投影到 𝑝 𝑝 p 的位姿处；
- 滑窗中点云约束是当前优化帧和局部地图特征匹配，因此特征对应的因子约束的是 𝑝 𝑝 p 帧和 𝑘 𝑘 k 帧( 𝑝 𝑝 p< 𝑘 𝑘 k<= 𝑗 𝑗 j)。
其优化模型为
min
X
1
2
{
∥
r
P
(
X
)
∥
2
+
∑
m
∈
m
L
α
α
∈
{
p
+
1
,
⋯
,
j
}
∥
r
L
(
m
,
X
)
∥
C
L
α
m
2
+
∑
β
∈
{
p
,
⋯
,
j
−
1
}
∥
r
B
(
z
β
+
1
β
,
X
)
∥
C
B
β
+
1
B
β
2
}
\begin{aligned} & \min _{\mathbf{X}} \frac{1}{2}\left\{\left\|\mathbf{r}_{\mathcal{P}}(\mathbf{X})\right\|^2+\sum_{\substack{m \in \mathbf{m}_{L_\alpha} \\ \alpha \in\{p+1, \cdots, j\}}}\left\|\mathbf{r}_{\mathcal{L}}(m, \mathbf{X})\right\|_{\mathbf{C}_{L_\alpha}^m}^2\right. \\ & \left.+\sum_{\beta \in\{p, \cdots, j-1\}}\left\|\mathbf{r}_{\mathcal{B}}\left(z_{\beta+1}^\beta, \mathbf{X}\right)\right\|_{\mathbf{C}_{B_{\beta+1}}^{B_\beta}}^2\right\} \end{aligned}
Xmin21⎩
⎨
⎧∥rP(X)∥2+m∈mLαα∈{p+1,⋯,j}∑∥rL(m,X)∥CLαm2+β∈{p,⋯,j−1}∑
rB(zβ+1β,X)
CBβ+1Bβ2⎭
⎬
⎫其中
r
P
(
X
)
\mathbf{r}_{\mathcal{P}}(\mathbf{X})
rP(X) 是边缘化产生的先验因子对应的残差；
r
L
(
m
,
X
)
\mathbf{r}_{\mathcal{L}}(m, \mathbf{X})
rL(m,X) 是点云特征匹配对应的残差；
r
B
(
z
β
+
1
β
,
X
)
\mathbf{r}_{\mathcal{B}}\left(z_{\beta+1}^\beta, \mathbf{X}\right)
rB(zβ+1β,X) 是IMU约束对应的残差。
4.2 具体流程
流程讲解思路：
• 以前述kitti中实现原理为基础，此处只是多了点云特征的约束；
• 只介绍可借鉴的内容，因此不介绍bias、外参初始化和外参优化等内容。
4.2.1 各类因子
-
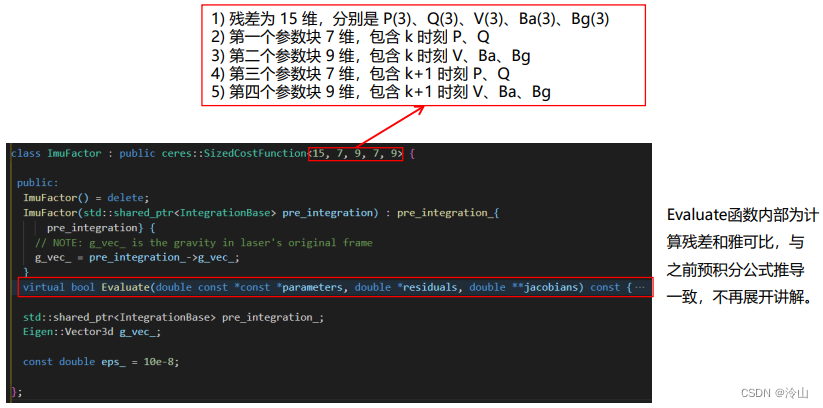
定义IMU 因子
-
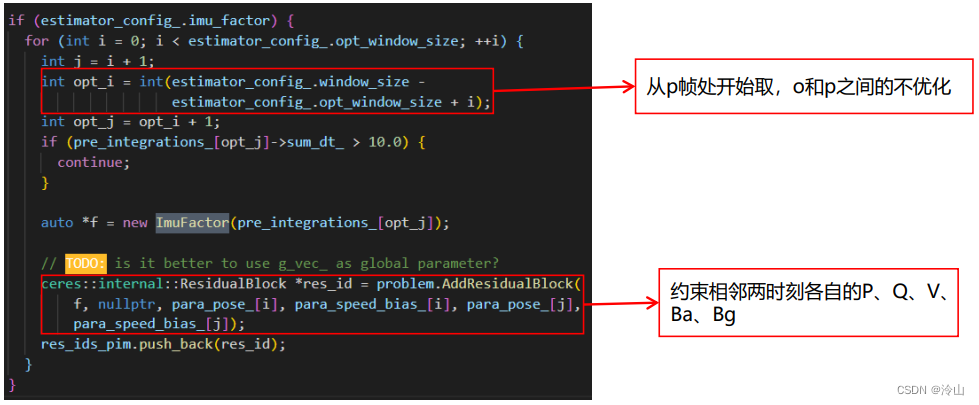
添加imu因子
-
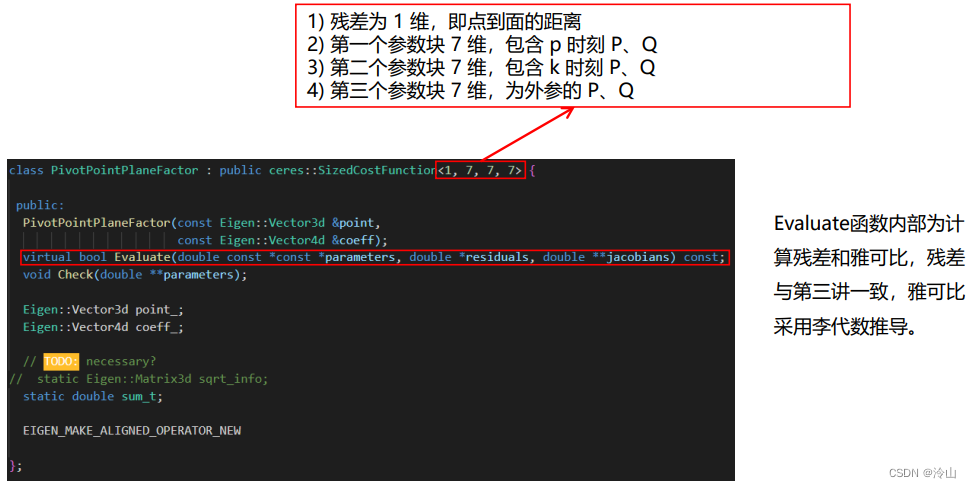
定义点云面特征因子
-
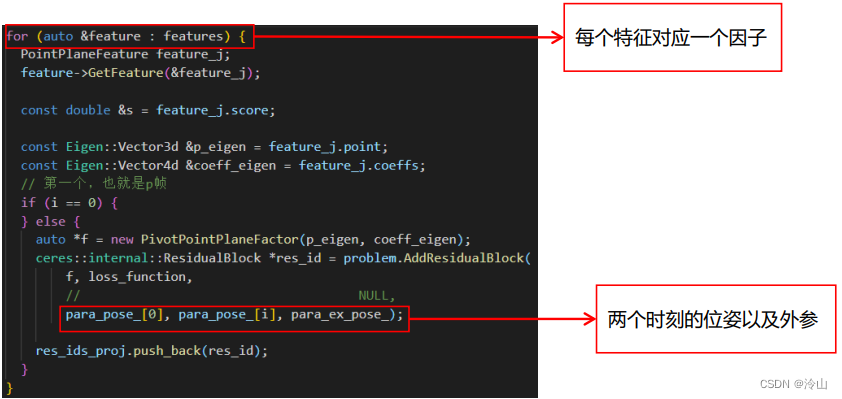
添加点云面特征
-
定义边缘化先验因子
由于不确定边缘化后会和哪些量产生关联，因此没有固定size。
其详细内容待讲解边缘化实现时再展开。 -
添加边缘化先验因子
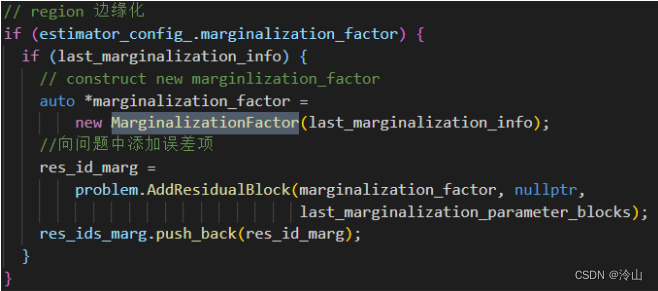
4.2.2 滑窗模型
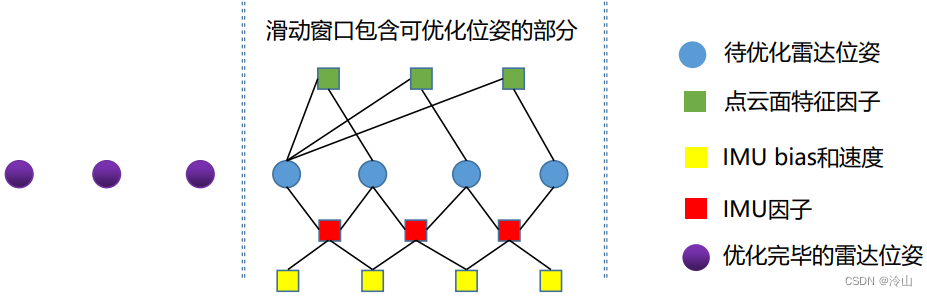
• 帧与帧之间通过特征约束，因此没有了激光里程计因子。
• 当前模型中没有使用点云的线特征。
-
IMU预积分和优化变量的残差
一个因子约束两个位姿，并约束两个时刻 IMU 的速度与 bias
残差关于优化变量的雅可比可视化如下：
因此对应的Hessian矩阵的可视化为：
-
点云面特征对应的残差
一个因子约束两个位姿
残差关于优化变量的雅可比可视化如下：
因此对应的Hessian矩阵的可视化为
-
完整模型
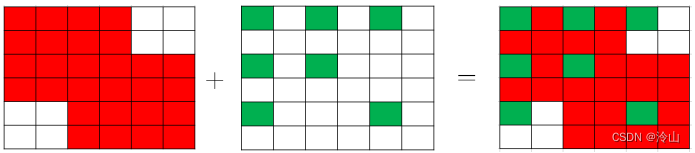以上工程，就是前述代码中添加各类因子到模型的过程。
4.2.3 边缘化
-
边缘化模型
需要边缘化掉的为方框中的变量 -
边缘化可视化
第一步：使用和要边缘化掉的量无关的因子，构建剩余变量对应的Hessian矩阵。
第二步：挑出和要边缘化掉的量相关的因子，构建待边缘化的Hessian矩阵，并使用舒尔补做边缘化。
对应的完整Hessian矩阵就是他们合在一起的结果。
-
边缘化实现
核心思路是把要边缘化掉的变量，以及跟这些变量被同一个因子约束的变量，汇总在一起。
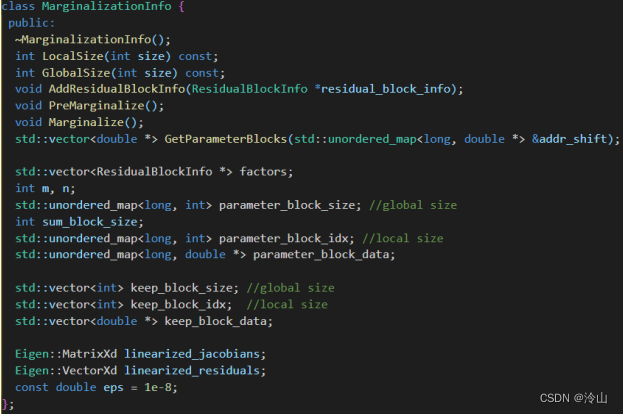
在该例中，把和模型无关的量去除，剩余部分如下(设每帧有20个面特征)
因此，放入MarginalizationInfo中的信息包括:
5个变量: T 0 M 0 T 1 M 1 T 2 T_0 \quad M_0 \quad T_1 \quad M_1 T_2 T0M0T1M1T2
41个因子： 40 个面特征因子、1个IMU因子
（此处假设的是第一次进行边缘化，若不是第 一次，因子中还应该有边缘化先验因子)
找出所有变量后，需要知道哪些是应该边缘化的，哪些是应该保留的。
右图代码中，形参里_parameter_blocks包含所有相关参数，而_drop_set即为这些参数中要边缘化掉的参数的id。
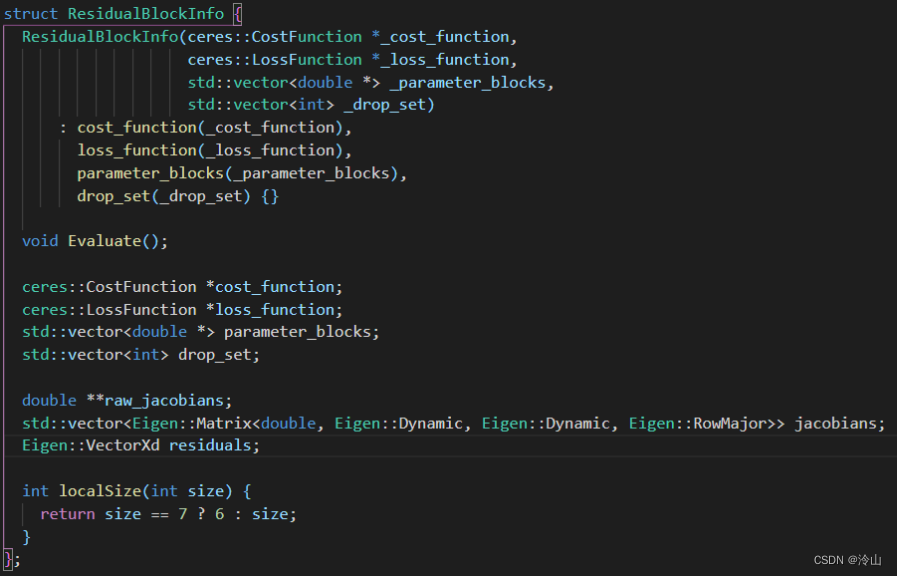
添加和IMU因子相关的ResidualBlockInfo
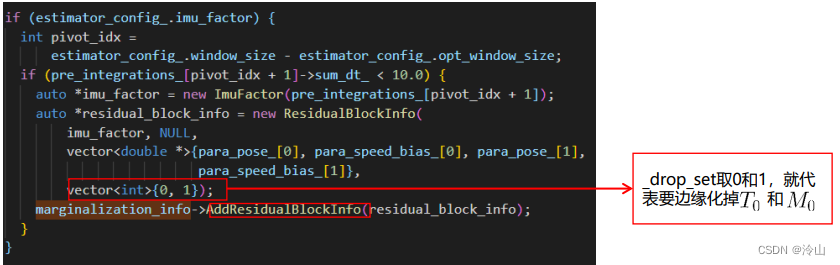
添加和面特征因子相关的ResidualBlockInfo
在添加以上ResidualBlockInfo的同时，核心变量parameter_block_size 就被赋值。
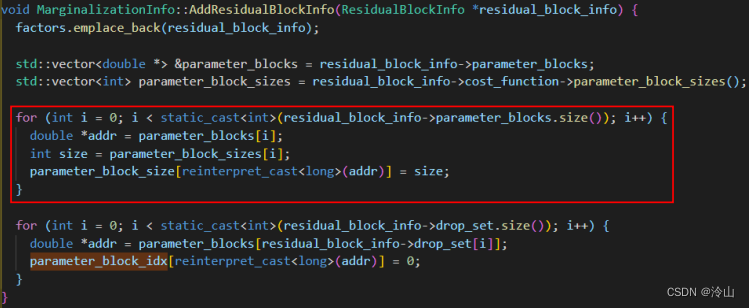
第二个核心函数的作用是计算每个因子对应的变量(parameter_blocks)、误差项(residuals)、雅可比矩阵(jacobians)，并把变量数值放到parameter_block_data中。
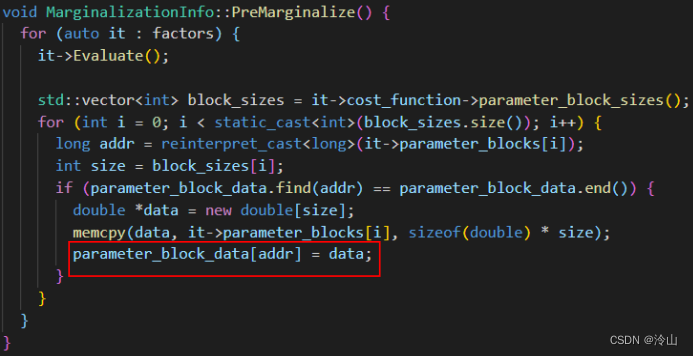
第三个核心函数的作用构建Hessian矩阵，Schur掉需要marg的变量，得到对剩余变量的约束，即为边缘化约束（先验约束）。
函数的前半部分，对m、n和parameter_block_idx 这三个核心变量进行了赋值。
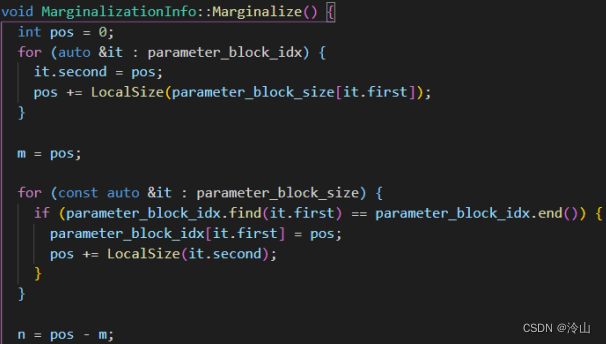
函数的中间部分开始构建Hessian 矩阵，由于使用多线程，因此要给不同的线程平均分配因子。
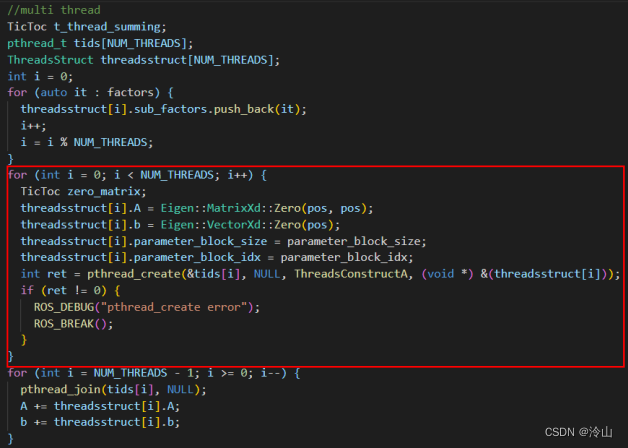
函数的最后便是执行边缘化，得到边缘化先验因子。
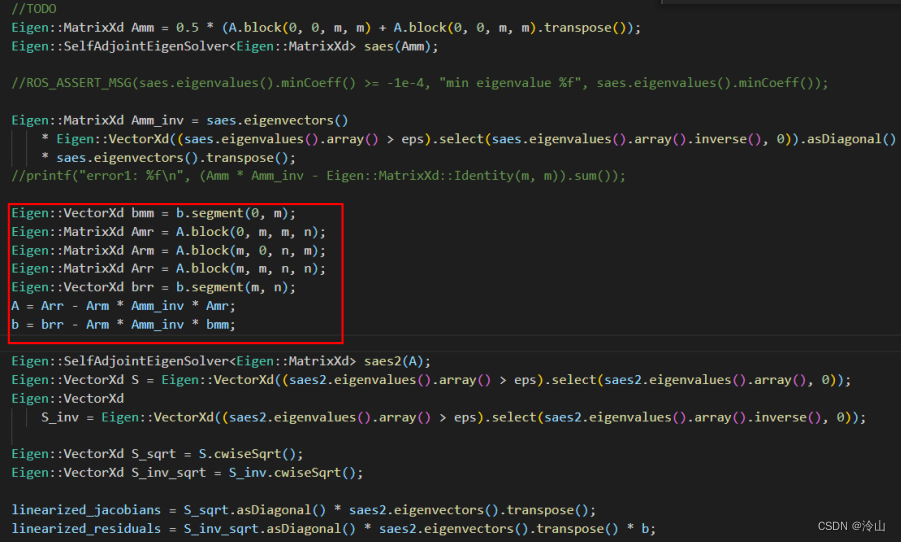
上述过程是假设第一次执行边缘化，当不是第一次时，步骤上只是多了在AddResidualBlockInfo时把边缘化先验因子也加入进来，剩余过程不变。
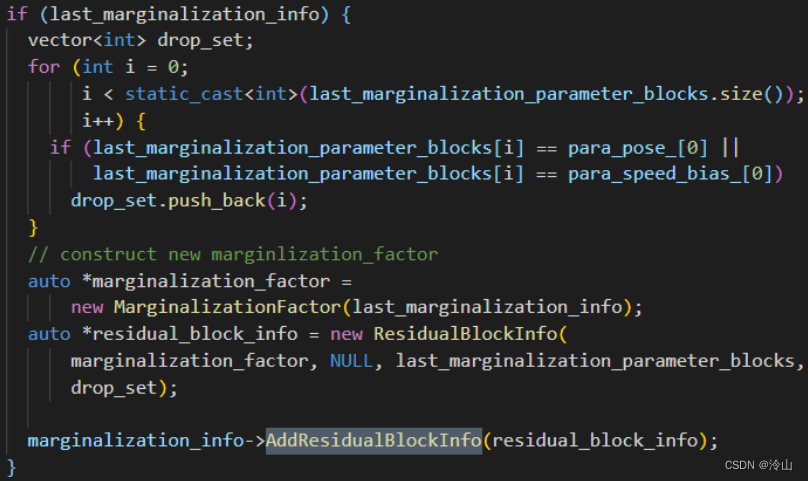
4.2.4 添加新帧
边缘化之后，模型如下：
注意：由于面特征因子都是和第一帧(
T
0
T_0
T0)关联，当它边缘化掉之后，该因子便不存在，因此在加入新的帧的同时，还需要构建所有帧和当前第一帧(
T
1
T_1
T1)的面特征关联。
添加新的帧以后，模型如下：
Hessian矩阵可视化如下：
此后不断循环该过程，便可以实现lio功能。
