🌼多年后再见你 - 乔洋/周林枫 - 单曲 - 网易云音乐 闲来无事听听歌
Dijkstra可解决“单源最短路径”问题
四种最短路算法
Floyd算法
时间复杂度高,但实现容易(5行核心代码),可解决负权边,适用于数据范围小的
Dijkstra算法
不能解决负权边,但具有良好扩展性,且复杂度较低
Bellman-Ford / 队列优化Bellman-Ford
可解决负权边,且复杂度较低
本节学习指定一个点(源点)到其他顶点的最短路径(单源最短路径)
比如下图,求1号顶点到2,3,4,5,6号顶点的最短路径

与Floyd-Warshall一样,我们依然采用二维数组e存储顶点和边的关系,初始值如下图:
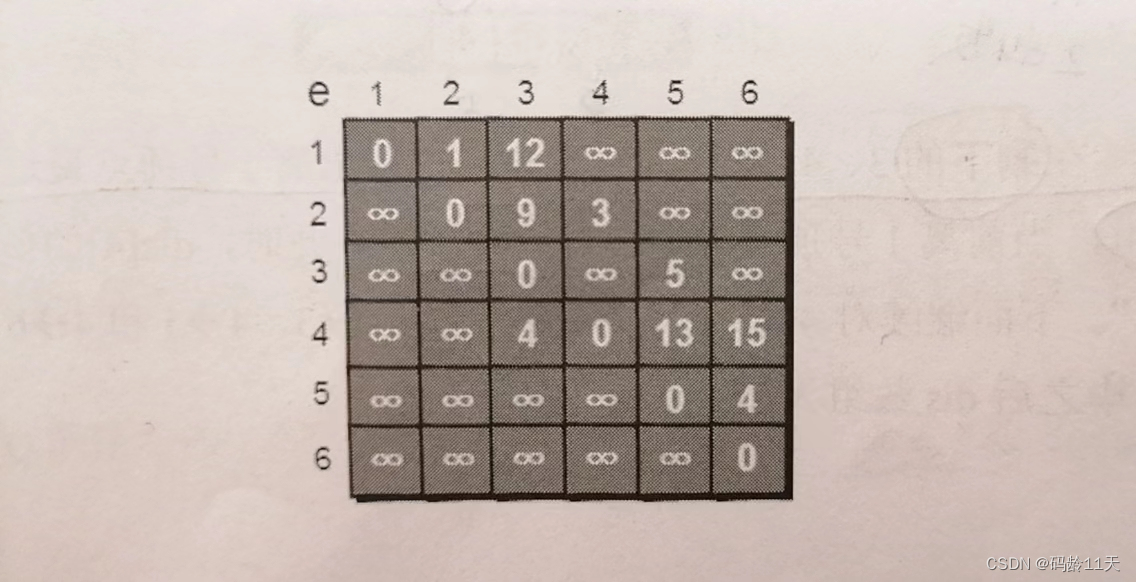
还需要一个一维数组dis(tant)来存储1号顶点到其他顶点的初始路程,如下图:

我们将此时dis数组中的值称为最短路程的“估计值”
第一步:找确定值 (1)
先找离源点(1号)最近的顶点,由dis数组可知,2号最近,选择2号顶点后,dis[2]的值就从“估计值”变成了“确定值”(表示1号到2号的最短路程已确定)
敲重点!
下面的推理是Dijkstra算法的核心, ↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
为什么确定了呢?因为:
1,离源点(1号顶点)最近的是2号顶点
2,这个图所有边都是正数
所以,通过其他顶点中转,使1号先经其他顶点,再到2号顶点的路程,肯定更长
所以此时dis[2]就是1号到2号最短路程的确定值
↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑
第二步:从刚被确定的顶点“出边”
第一步确定了一个确定值,第二步我们从这个被确定的点,进行“出边”,有2->3, 2->4两条边
先判断 dis[2] + e[2][3] < dis[3],即判断能否借2号中转,使1号到3号的路程缩短,由下图可知,dis[2] + e[2][3] == 1 + 9等于10,dis[3] == 12,可以缩短,所以dis[3]更新为10
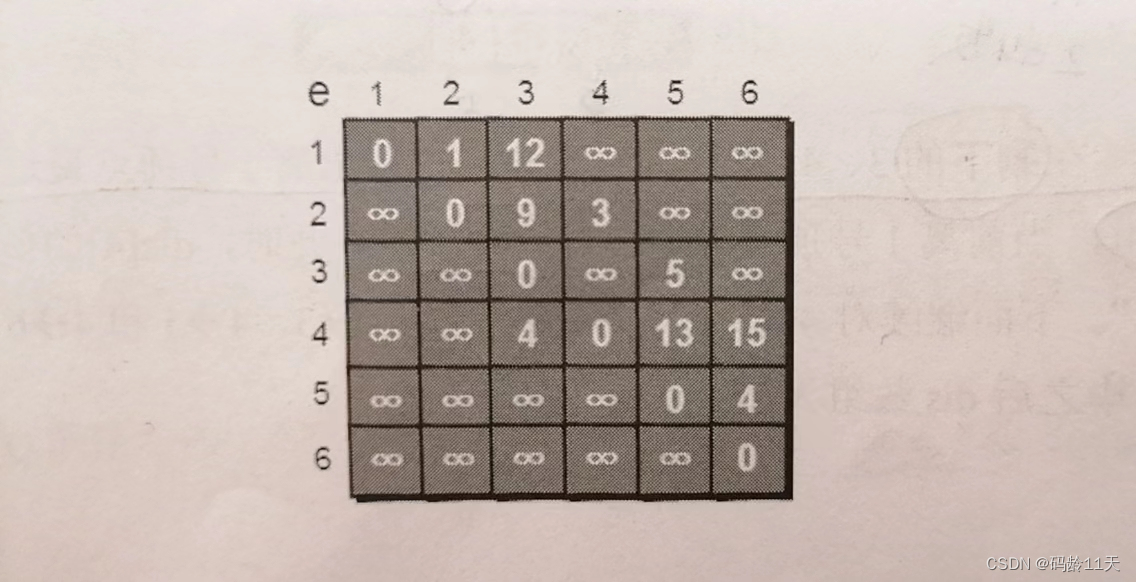

这个过程有个专业术语叫“松弛” ,即1号顶点到3号顶点的路程dis[3],通过2->3这条边“松弛”成功,这便是Dijkstra算法的主要思想:
通过“边”来松弛1号顶点到其他顶点的路程
同理,判断dis[2] + e[2][4] < dis[4],dis[2] + e[2][4] == 1 + 3等于4,dis[4] == ∞
4 < ∞,所以dis[4]更新为4

围绕确定点2的出边结束,开始下一轮找确定点
第一步:找确定值 (2)
从剩下未确定的3,4,5,6号顶点,选出离1号最近的点,通过上面更新后的dis数组,当前最近的是4号顶点,所以dis[4]从估计值变成确定值
为什么此时dis[4]就确定是1号到4号的最短路径了呢?因为dis数组更新后,假设存在经一个或几个点中转,路程比dis[4]小,首先经2号中转后离1号顶点最近的点已确定,就是4号,所以不存在经2号中转比dis[4]小的
至于经3,5,6中转比dis[4]小,更不存在了,此时1到3,5,6不经中转都比dis[4]大
所以更新后的dis[4]必然确定了
第二步:从刚被确定的顶点“出边”


从被确定的4号顶点出边,4->3, 4->5, 4->6,
dis[4] + e[4][3] < dis[3](8 < 10),dis[4] + e[4][5] < dis[5](17 < ∞),dis[4] + e[4][6] < dis[6](19<∞)
出边完毕后,看下图:

第一步:找确定值 (3)
再在剩下未确定的3, 5, 6中,找出离1号最近的,即dis中未确定中的最小值,8 < 17 < 19
所以dis[3]从估计值变为确定值
第二步:从刚被确定的顶点“出边”

只能从3向5出边,3不和6直接相连(不能出边),只能3->5了,dis[3] + e[3][5] == 8 + 5 == 13
dis[5] == 17, 13 < 17,所以dis[5]更新为13
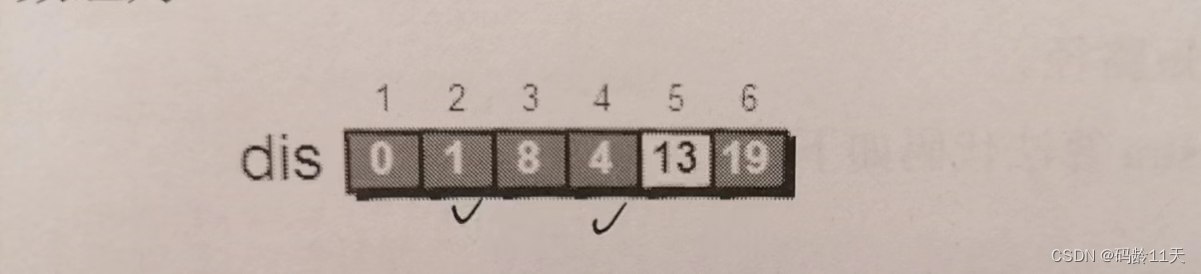
第一步:找确定值 (4)
从剩下的5,6号找离1号最近的顶点,是5号,dis[5]从估计值变成确定值
第二步:从刚被确定的顶点“出边”
dis[5] + e[5][6] < dis[6](17 < 19),dis[6]更新为17

第一步:找确定值 (5)
在剩下的6号中找离1号最近的,就他一个了,所以dis[6]从估计值变确定值
第二步:从刚被确定的顶点“出边”
没有未确定的值,出边失败~ 算法结束
最终

这便是1号顶点到其他顶点的最短路径,至此,“单源最短路径”问题解决
思路
每次找到离源点最近的点,以该点为中心对未确定的点进行扩展
1,
将所有顶点分为两部分,一部分已确定(确定值),一部分未确定(估计值)
已确定的顶点,用book数组标记为1,比如book[4] = 1
2,
将某一点到源点最短路径用dis数组保存;二维数组e中,i 到 j 无法到达用e[i][j] = ∞来表示,i 到 i 用e[i][i] = 0来表示
完整代码
#include<cstdio>
int main()
{
int e[10][10], dis[10], book[10], i, j, n, m;
int t1, t2, t3, u, v, Min;
int inf = 1e8; //infinity(n.)无穷
//读入n个顶点, m条边
scanf("%d%d", &n, &m);
//初始化
for(i = 1; i <= n; ++i)
for(j = 1; j <= n; ++j) {
if(i == j) e[i][j] = 0;
else e[i][j] = inf;
}
//读入边
for(i = 1; i <= m; ++i) {
scanf("%d%d%d", &t1, &t2, &t3);
e[t1][t2] = t3;
}
//初始化dis数组, 表示源点1号到其他点初始路程
for(i = 1; i <= n; ++i)
dis[i] = e[1][i];
//初始化book数组
for(i = 1; i <= n; ++i)
book[i] = 0;
//Dijkstra算法核心
//源点不用确定, 所以是n - 1次遍历
for(i = 1; i <= n - 1; ++i) {
Min = inf;
for(j = 2; j <= n; ++j) { //从顶点2开始
//找确定值(未确定中找最小值)
if(book[j] == 0 && dis[j] < Min) {
Min = dis[j];
u = j;
}
}
book[u] = 1; //顶点u已确定
//从刚被确定的顶点出边
for(v = 2; v <= n; ++v) //从顶点2开始
if(e[u][v] < inf && dis[u] + e[u][v] < dis[v])
//两点连通且可更新
dis[v] = dis[u] +e[u][v];
}
for(int i = 1; i <= n; ++i)
printf("%d ", dis[i]);
return 0;
}
输入输出
6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
0 1 8 4 13 17由上述代码,可知Dijkstra时间复杂度为O(n^2)
每次找到离源点最近顶点的时间复杂度是O(n),这里我们可以用堆来优化(下下个博客讲)
使找最近顶点的复杂度从O(n) --> O(logn)
另外对于边数m小于n^2的稀疏图来说(我们称m < n^2的图为稀疏图,m > n^2的图为稠密图)
可以用邻接表来代替矩阵,使整个算法时间复杂度优化到O((m + n) * logn),但稀疏图的最坏情况是m == n^2,此时 (m + n) * logn 比 n^2 还大
当然大多数情况不会有那么多边
下面这个是稠密图

总结
每次出边就要判断,判断dis[a] + e[a][c] < dis[c]成立,就要更新dis[c] = dis[a] + e[a][c]
即源点 -> a -> c的路程 小于 源点 -> c的路程 ,其中dis[a]是确定值