文章目录
- 方向角与方向余弦
- 方向角
- 方向余弦
- 方向导数
- 定义
- 性质
- 梯度下降
梯度下降法(Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
方向角与方向余弦
方向角
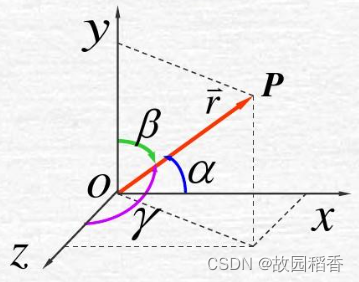
向量(或有向直线)与坐标轴正向或基向量的交角称为向量的方向角。定义域为
[
0
,
π
]
[0,\pi]
[0,π]。
方向余弦
{
cos
α
=
x
∣
r
∣
cos
β
=
y
∣
r
∣
cos
γ
=
z
∣
r
∣
\begin{cases} \cos\alpha = \frac{x}{|r|}\\ \cos\beta = \frac{y}{|r|}\\ \cos\gamma = \frac{z}{|r|} \end{cases}
⎩
⎨
⎧cosα=∣r∣xcosβ=∣r∣ycosγ=∣r∣z
且有
cos
2
α
+
cos
2
β
+
cos
2
γ
=
1
\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1
cos2α+cos2β+cos2γ=1
方向导数
定义
给定标量函数
f
(
x
,
y
,
z
)
f(x,y,z)
f(x,y,z),和任意向量
l
⃗
\vec{l}
l,该向量与三个坐标轴的夹角分别为
α
\alpha
α、
β
\beta
β、
γ
\gamma
γ,从定义域中一定
P
0
(
x
,
y
,
z
)
P_0(x,y,z)
P0(x,y,z)出发,沿着向量
l
⃗
\vec{l}
l方向移动距离
Δ
s
\Delta s
Δs,到达点
P
1
(
x
+
Δ
s
cos
α
,
y
+
Δ
s
cos
β
,
z
+
Δ
s
cos
γ
)
P_1(x+\Delta s \cos\alpha,y+\Delta s \cos\beta,z+\Delta s \cos\gamma)
P1(x+Δscosα,y+Δscosβ,z+Δscosγ),定义方向导数:
d
f
d
l
⃗
=
lim
Δ
s
→
0
f
(
x
+
Δ
s
cos
α
,
y
+
Δ
s
cos
β
,
z
+
Δ
s
cos
γ
)
−
f
(
x
,
y
,
z
)
Δ
s
\frac{df}{d\vec{l}}=\lim_{\Delta s \to 0}\frac{f(x+\Delta s \cos\alpha,y+\Delta s \cos\beta,z+\Delta s \cos\gamma)-f(x,y,z)}{\Delta s}
dldf=limΔs→0Δsf(x+Δscosα,y+Δscosβ,z+Δscosγ)−f(x,y,z)
代表函数 f f f在方向 l ⃗ \vec{l} l的变化率。
性质
d f d l ⃗ = ∂ f ∂ x cos α + ∂ f ∂ y cos β + ∂ f ∂ z cos γ = ( ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z ) ⋅ ( cos α , cos β , cos γ ) = ∇ f ⋅ n ⃗ = ∣ ∇ f ∣ cos ⟨ ∇ f , l ⃗ ⟩ \begin{aligned} \frac{df}{d\vec{l}} &=\frac{\partial f}{\partial x}\cos\alpha+\frac{\partial f}{\partial y}\cos\beta+\frac{\partial f}{\partial z}\cos\gamma \\ \\ &=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})\cdot(\cos\alpha,\cos\beta,\cos\gamma)=\nabla f \cdot\vec{n}=|\nabla f|\cos\lang\nabla f,\vec{l}\rang \end{aligned} dldf=∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ=(∂x∂f,∂y∂f,∂z∂f)⋅(cosα,cosβ,cosγ)=∇f⋅n=∣∇f∣cos⟨∇f,l⟩
当 l ⃗ \vec{l} l取 f f f的梯度方向时, cos ⟨ ∇ f , l ⃗ ⟩ = 1 \cos\lang\nabla f,\vec{l}\rang=1 cos⟨∇f,l⟩=1,变化率绝对值最大且为正;当 l ⃗ \vec{l} l取 f f f的负梯度方向时, cos ⟨ ∇ f , l ⃗ ⟩ = − 1 \cos\lang\nabla f,\vec{l}\rang=-1 cos⟨∇f,l⟩=−1,变化率绝对值最大且为负。
梯度下降
应用场景:求损失函数的最小值。
梯度下降的具体算法实现过程是:
1、确定模型和损失函数;
2、参数初始化,包括:参数、算法终止条件和步长;
3、参数更新
θ
j
+
1
=
θ
j
−
α
∂
J
∂
θ
j
\theta_{j+1}=\theta_j - \alpha \frac{\partial J}{\partial\theta_j}
θj+1=θj−α∂θj∂J
4、判断停止条件,若满足,则停止,若不满足,则继续更新。



![[Java 进阶] synchronized 与 ReentrantLock的区别](https://img-blog.csdnimg.cn/6fff8d64b4a04f89935dcc4bf57350d0.png)