1、傅里叶变换

a、傅里叶变换原理

时域分析：以时间为参照进行分析。

频域分析：相当于上帝视角一样，看事物层次更高，时域的运动在频域来看就是静止的。

eg：投球——时域分析：第1分钟投了3分，第2分钟投了2分，第3分钟投了1分......第n分钟投了2分。

频域分析：每隔一分钟投一个3分球，每隔一分钟投一个2分球。

关于傅里叶变换详细描述可以参考知乎上的这篇文章：

文章链接：https://zhuanlan.zhihu.com/p/19763358

傅里叶变换的作用： 低频——变化缓慢的灰度分量

高频——变化剧烈的灰度分量

滤波： 低通滤波器——只保留低频，会使得图像模糊

高通滤波器——只保留高频，会使得图像细节增强

频域转换代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread("lena.jpg",0)
img_float32=np.float32(img)
dft=cv2.dft(img_float32,flags=cv2.DFT_COMPLEX_OUTPUT)#图像转为频域,输入图像需要先转化为float32格式
dft_shift=np.fft.fftshift(dft)
#得到灰度图表现的形式
magnitude_spectrum=20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1])
plt.subplot(121)
plt.imshow(img,cmap='gray')
plt.title("input image")
plt.xticks([])
plt.yticks([])
plt.subplot(122)
plt.imshow(magnitude_spectrum,cmap='gray')
plt.title("magnitude spectrum")
plt.xticks()
plt.yticks()
plt.show()

b、低通与高通滤波

低通滤波代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread("lena.jpg",0)
img_float32=np.float32(img)
dft=cv2.dft(img_float32,flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift=np.fft.fftshift(dft)
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #中心位置
mask=np.zeros((rows,cols,2),np.uint8)#创建掩膜,进行低通滤波
mask[crow-30:crow+30,ccol-30:ccol+30]=1
fshift=dshift*mask
f_isift=np.fft.fftshift(fshift)
img_back=cv2.idft(f_ishift)#将图像转回去，和dft为互逆运算
img_back=cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
plt.subplot(121)
plt.imshow(img,cmap='gray')
plt.title("input image")
plt.xticks([])
plt.yticks([])
plt.subplot(122)
plt.imshow(img_back,cmap='gray')
plt.title("result1")
plt.xticks()
plt.yticks()
plt.show()

高通滤波代码:

import cv2
import numpy as np
import matplotlib.pyplot as plt
img=cv2.imread("lena.jpg",0)
img_float32=np.float32(img)
dft=cv2.dft(img_float32,flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift=np.fft.fftshift(dft)
rows,cols=img.shape
crow,ccol=int(rows/2),int(cols/2) #中心位置
mask=np.ones((rows,cols,2),np.uint8)#创建掩膜,进行低通滤波
mask[crow-30:crow+30,ccol-30:ccol+30]=0
fshift=dshift*mask
f_isift=np.fft.fftshift(fshift)
img_back=cv2.idft(f_ishift)#将图像转回去，和dft为互逆运算
img_back=cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
plt.subplot(121)
plt.imshow(img,cmap='gray')
plt.title("input image")
plt.xticks([])
plt.yticks([])
plt.subplot(122)
plt.imshow(img_back,cmap='gray')
plt.title("result1")
plt.xticks()
plt.yticks()
plt.show()

2、直方图

直方图：横坐标为像素值，从左到右即从0到255，纵坐标为每个像素值在图像中出现的次数。

单通道直方图代码：

import matplotlib.pyplot as plt
import cv2
img=cv2.imread("cat.jpg",0)#0代表灰度图
hist=cv2.calcHist([img],[0],None,[256],[0,256])#参数从左到右依次为图像、通道（012,BGR）、掩膜图像、histsize（BIN数量）、像素值范围
hist.shape
plt.hist(img.ravel(),256)
plt.show()

三个通道直方图代码：

img=cv2.imread("cat.jpg")
color=['b','g','r']
for i col in enumerate(color):
    histr=cv2.calcHist([img],[i],None,[256],[0,256])
    plt.plot(histr,color=col)
    plt.xlim([0,256])
    plt..show()

3、掩膜图像

创建掩膜代码：

import numpy as np
mask=np.zeros(img.shape[:2],np.uint8)
mask[100:300,100:400]=255
cv2.imshow("mask",mask)
cv2.waitKey()
cv2.destroyAllWindows()

掩膜操作:

mask_img=cv2.bitwise_and(img,img,mask=mask)#与操作
cv2.imshow("mask_img",mask_img)
cv2.waitKey()
cv2.destroyAllWindows()

计算掩膜操作的直方图:

hist_mask=cv2.calcHist([img],[0],mask,[256],[0,256])
plt.plot(hist_mask)
plt.xlim([0,256])
plt.show()

4、直方图均衡化

a、均衡化原理及计算方法

均衡化：让原本分布不均衡的直方图在坐标轴上变得更为均衡，如下图所示。

均衡化计算过程：

步骤1：原图像灰度值统计

步骤2：每个灰度的个数、概率及累积概率（累积概率：加上前面几个像素点的概率，如：0.1875+0.25=0.4375）

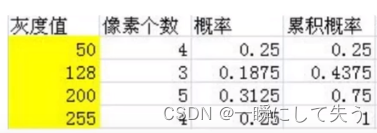
步骤3：累积概率*灰度值取值范围（0.25*（255-0））

步骤4：均衡化后的灰度值统计

b、均衡化代码及效果

均衡化前的直方图展示：

img=cv2.imshow("cat.jpg")
plt.hist(img.ravel(),256)
plt.show()

均衡化代码：

equ=cv2.equalizeHist(img)
plt.hist(img.ravel(),256)
plt.show()

自适应均衡化:

clahe=cv2.createCLAHE(clipLimit=2.0,tileGridSize=(8,8))
res_clahe=clahe.apply(img)
res=np.hstack((img,equ,res_clahe))
cv2.imshow("res",res)
cv2.waitKey()
cv2.destroyAllWindows()