安装 ts运行环境 node

node-v看版本号
2. 安装ts -g全局安装

npm i -g typescript  // 这里全局安装  -s安装无法使用tsc

创建一个01.ts文件
命令编译这个.ts文件

tsc 01.ts

这时候文件多了一个01.js文件

TS类型

| 类型 | 例子 |

类型	例子	描述

number	1, -33, 2.5	任意数字
string	‘hi’, “hi”, hi	任意字符串
boolean	true、false	布尔值true或false
字面量	其本身	限制变量的值就是该字面量的值
any	*	任意类型
unknown	*	类型安全的any
void	空值（undefined）	没有值（或undefined）
never	没有值	不能是任何值
object	{name:‘孙悟空’}	任意的JS对象
array	[1,2,3]	任意JS数组
tuple	[4,5]	元素，TS新增类型，固定长度数组
enum	enum{A, B}	枚举，TS中新增类型

数字、字符串和布尔类型

let decimal: number = 6;   //6
let isDone: boolean = false;


let fullName: string = `Bob Bobbington`;
let sentence: string = `Hello, my name is ${fullName}`  
//'Hello, my name is Bob Bobbington'

tsc 转js后
var fullName = "Bob Bobbington";
var sentence = "Hello, my name is ".concat(fullName);

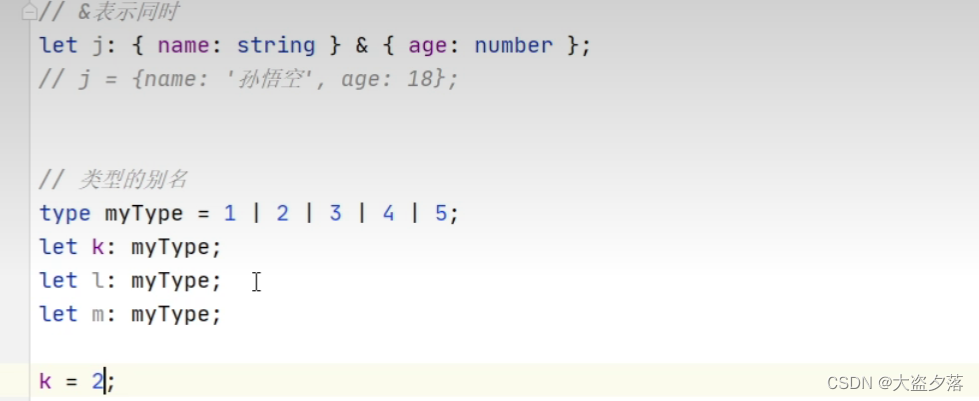
字面量

可以使用字面量去指定变量的类型，也可以通过字面量可以确定变量的取值范围

let a:10 
a = 11   //报错  
a = 10  //正确

let color: 'red' | 'blue' | 'black'; //color 取值范围内正确,其它的都报错
let num: 1 | 2 | 3 | 4 | 5;

any 和unknown

let d: any = 4;
d = 'hello';
d = true;

let notSure: unknown = 4;
     notSure = 'hello';

any 赋值给另外一个变量不报错，unknown 赋值给另外一个变量会报错
unknown 是一个类型安全的any，

let s:string="df"
let d:any ="dse"
let f:unknown="sdfwe"
s = d  //不报错
s = f  //报错

类型断言

可以用类型断言来赋值不报错

s=f as string  
//or
s = <string>f

第一种用法

let someValue: unknown = "this is a string";
let strLength: number = (someValue as string).length;

第二种用法

let someValue: unknown = "this is a string";
let strLength: number = (<string>someValue).length;

void和never

用在函数中，void 表示没有返回值的函数，如果有return 10 会报错

let unusable: void = undefined;

function fn() :void {
  return 10  ; //报错
  return  //不报错
}

never表示永远不会有结果，一般用来抛出异常

function error(message: string): never {
    throw new Error(message);
}

object

? 表示属性是可选的

let bb: {name:string,age?:number}  //在属性后面加上 ? 表示属性是可选的
bb={name:'ded'}

[propname:string]:any 表示任意类型的属性，属性名是字符串，属性值任意类型
propname可以随便写，任意名称替换都可以

let  cc:{name:string,[propname:string]:any}
cc = {name:'dsd',age:18,gender:'男'}

设置函数结构的类型声明

语法:(形参：类型，形参：类型...)=> 返回值
let dd:(a:number,b:number)=>number
dd =function(ni,n2):number{
    return 10
}

Array

两种声明方式

let arr1:string[]
arr1=['a','b','c']

let arr2:Array<number>
arr2=[1,2,3]

tuple 元组

元组就是固定长度的数组

let x: [string, number];
x = ["hello", 10];

enum 枚举

enum Color {
  Red,
  Green,
  Blue,
}
let c: Color = Color.Green;

enum Color {
  Red = 1,
  Green,
  Blue,
}
let c: Color = Color.Green;

enum Color {
  Red = 1,
  Green = 2,
  Blue = 4,
}
let c: Color = Color.Green;