第五十章 动态规划——数位DP模型
- 一、什么是数位DP
- 数位DP的识别
- 数位DP的思路
- 二、例题
- 1、AcWing 1083. Windy数(数位DP)
- 2、AcWing 1082. 数字游戏(数位DP)
- 3、AcWing 1081. 度的数量(数位DP)
一、什么是数位DP
数位DP的识别
当一道题问我们,数轴上,某个区间内的数,满足某个条件的个数。
一般像这种题我们会使用数位DP的逻辑。
数位DP的思路
数位DP顾名思义就是按照数字的每一位去讨论。
那么数位DP做题思路分为两步:按位枚举,分类讨论

我们把区间的上限X写出来:
那么怎么分类讨论呢?
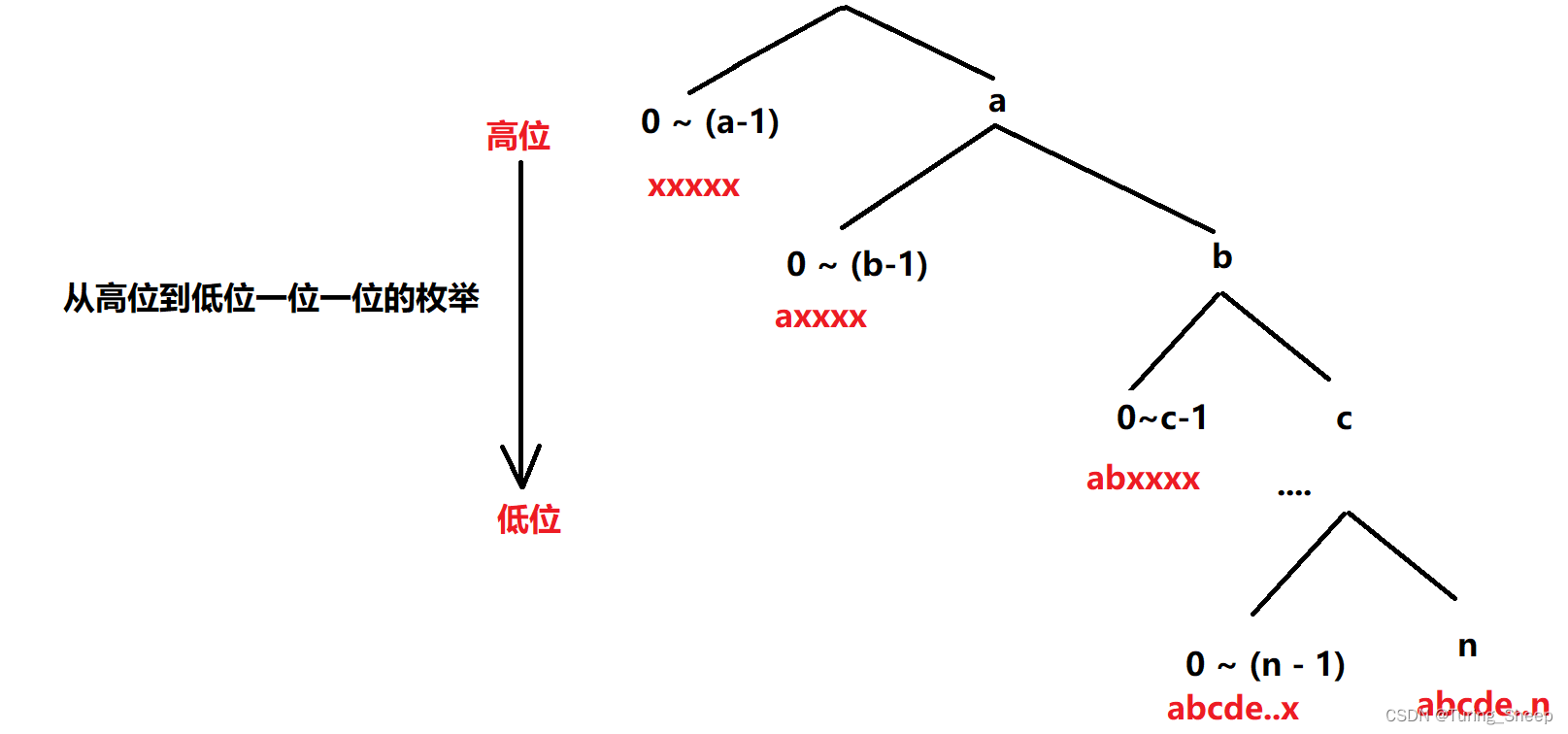
从上到下是从高位到低位枚举的,对于每一位我们的分类依据是:(0 ~ a - 1)和a,那么为什么这么分呢?
一般数位DP都是让我们挑选满足某个条件的数,我们不仅需要考虑某个数是否满足条件,还需要考虑某个数是否小于上限值。
那么我们在分类讨论以后,就发现我们分出的第一类情况中:0~a-1,由于高位都小于了a,那么这个数肯定比上限X小,也就是说此时我们只需要考虑是否满足题目中的某个条件。
我们对每一位都做这样的操作,只不过越往下分,每个数字固定的前缀就越长,最后我们会发现所有二叉树的右儿子恰好组成了我们上限值。
那么有人可能会想,题目中问的有可能是个区间,难道我们不需要考虑这个数必须大于等于下限吗?
这里可以使用一个思路,假设 f [ n ] f[n] f[n]是满足所有小于等于上限值的数的数量,我们只需要再减去小于下限m的数目,即 f [ m − 1 ] f[m - 1] f[m−1]的值,就是区间 [ n , m ] [n,m] [n,m]内符合题目条件的数目。
我们发现上面介绍的仅仅是分类讨论,那和DP有什么关系呢?
其实当我们进行分类讨论后,我们发现左支部分枚举的数是不需要关注他的大小是否超过区间上限的,因此我们只需要考虑它是否满足某个条件,而找出符合该条件的数目的时候往往需要用DP。
二、例题
1、AcWing 1083. Windy数(数位DP)
这道题中要格外注意前导零的问题。
AcWing 1083. Windy数(数位DP)
2、AcWing 1082. 数字游戏(数位DP)
AcWing 1082. 数字游戏(数位DP)
3、AcWing 1081. 度的数量(数位DP)
AcWing 1081. 度的数量(数位DP)