梯度下降
梯度下降法是常用于求解无约束情况下凸函数的极小值,是一种迭代类型的算法,因为凸函数只有一个极值点,故求解出来的极小值点就是函数的最小值点
公式

第一个θ,是更新之后的θ,第二个θ是更新之前的θ,求偏导也是更新之前的θ,
需要对θ设置一个初始化的值,
α是学习率,α过大,可能会产生振荡,导致找不到极值点,甚至可能反向更新
α过小,会导致在限制的迭代次数之内没有找到极值点
迭代终止条件:偏差不再下降或下降很小,即误差控制在限定范围内;或迭代达到迭代次数上限要求
相关算法
SDG(随机梯度下降算法):随机选取单个样本的θ值作为当前模型的θ更新,每次迭代只计算一个样本梯度

BGD(批量梯度下降算法):选取所有样本的θ值作为当前模型的θ值更新,每次迭代计算所有样本的梯度

MBGD(小批量梯度下降算法):选取部分样本的θ值作为当前模型的θ值更新,每次迭代计算部分样本的梯度
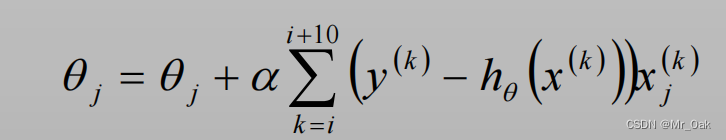
总结:
SGD的迭代次数更少
由于SGD是随机选取的样本,所以有可能跳出局部最优解
SGD和MBGD可能会出现波动
BGD一定能得到最优解,由于SGD的随机性,且每次迭代一个样本,在有限迭代次数内可能看不到最优解
案例
对一元函数的收敛案例
import sys
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import random
# 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
x = 100
input_x = np.arange(x) * 0.1
m = 10
step_max = 150
learn_rate = 0.0003
true_y = 5 * input_x
def pre_y(x, k):
return k * x
# SDG
K = 0.0
G_KS = [0.0]
for step in range(step_max):
x1_num = np.random.randint(len(input_x))
tidu = (pre_y(input_x[x1_num], K) - true_y[x1_num]) * input_x[x1_num]
K -= learn_rate * tidu
G_KS.append(K)
# print(G_KS)
# BGD
K = 0.0
G_KB = [0.0]
for step in range(step_max):
sum_tidu = 0
for i in range(len(input_x)):
tidu = (pre_y(input_x[i], K) - true_y[i]) * input_x[i]
sum_tidu += tidu
K -= learn_rate * sum_tidu
G_KB.append(K)
# print(G_KB)
# MBGD
K = 0.0
G_KM = [0.0]
for step in range(step_max):
sum_tidu = 0
r_n = random.sample(range(0, len(input_x)), m)
# print(r_n)
for i in r_n:
tidu = (pre_y(input_x[i], K) - true_y[i]) * input_x[i]
sum_tidu += tidu
K -= learn_rate * sum_tidu
G_KM.append(K)
# print(G_KM)
## 画图
plt.figure(facecolor='w')
plt.plot(range(step_max + 1), G_KS, 'r', label='SGD')
plt.plot(range(step_max + 1), G_KB, 'b', label='BGD')
plt.plot(range(step_max + 1), G_KM, 'k', label='MBGD')
plt.legend(loc='lower right')
plt.title('一维函数不同梯度下降对比')
plt.xlabel('step')
plt.ylabel('K')
plt.show()
结果显示