- 104.二叉树的最大深度 559.n叉树的最大深度
- 111.二叉树的最小深度
- 222.完全二叉树的节点个数
104.二叉树的最大深度
力扣题目链接
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7],

返回它的最大深度 3 。
var maxDepth = function(root) {
if(root == null) return 0;
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
};
var root = {
val: 3,
left: {
val: 9,
left: null,
right: null
},
right: {
val: 20,
left: {
val: 15,
left: null,
right: null
},
right: {
val: 7,
left: null,
right: null
}
}
}
console.log(maxDepth(root));递归法
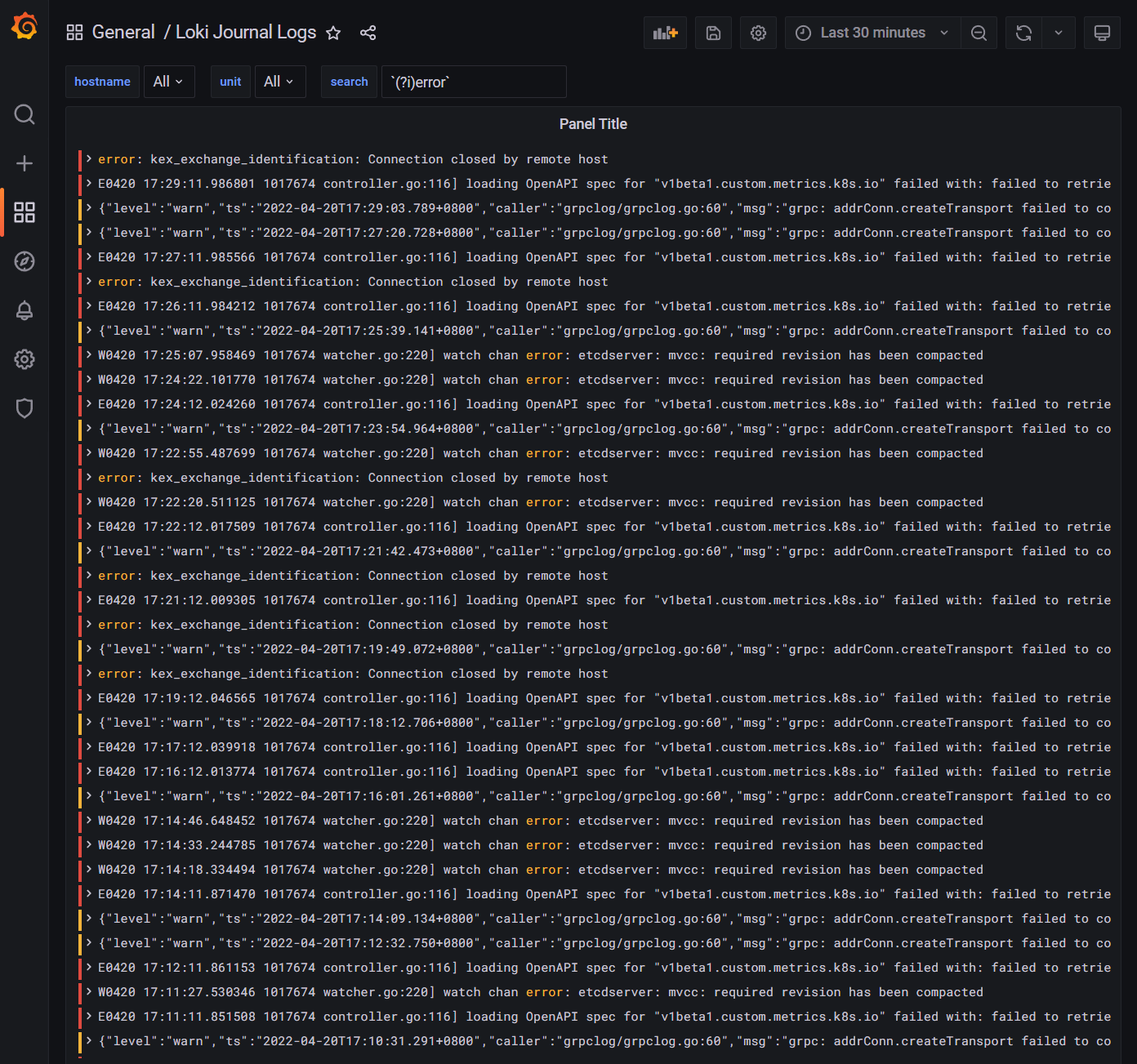
本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,使用后序求的是高度。
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)
而根节点的高度就是二叉树的最大深度,所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
我先用后序遍历(左右中)来计算树的高度。
// 代码随想录
var maxdepth = function(root) {
if (root === null) return 0;
return 1 + Math.max(maxdepth(root.left), maxdepth(root.right))
};
// 二叉树最大深度递归遍历
var maxdepth = function(root) {
//使用递归的方法 递归三部曲
//1. 确定递归函数的参数和返回值
const getdepth = function(node) {
//2. 确定终止条件
if(node === null) {
return 0;
}
//3. 确定单层逻辑
let leftdepth = getdepth(node.left);
let rightdepth = getdepth(node.right);
let depth = 1 + Math.max(leftdepth, rightdepth);
return depth;
}
return getdepth(root);
};迭代法
使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
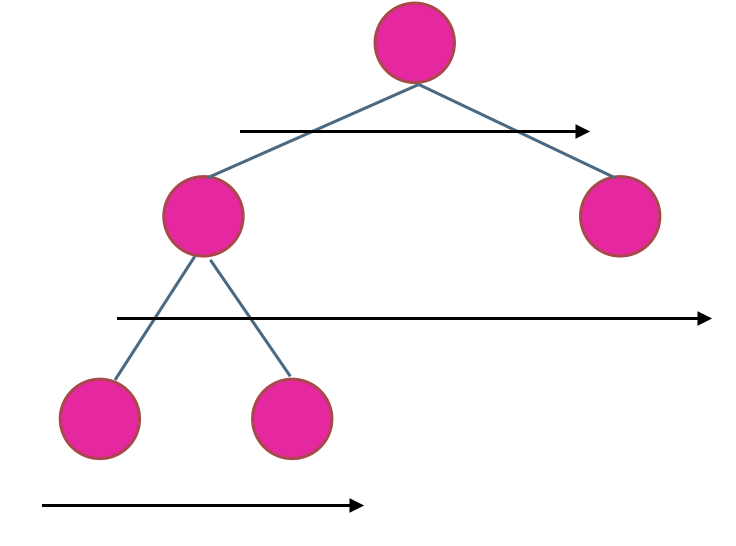
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
如果对层序遍历还不清楚的话,可以看这篇:二叉树:层序遍历登场!
// 二叉树最大深度层级遍历
var maxDepth = function(root) {
if(!root) return 0
let count = 0
const queue = [root]
while(queue.length) {
let size = queue.length
/* 层数+1 */
count++
while(size--) {
let node = queue.shift();
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return count
};
559.n叉树的最大深度
力扣题目链接
给定一个 n 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
例如,给定一个 3叉树 :

我们应返回其最大深度,3。
思路:
依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
// 559.n叉树的最大深度
// N叉树的最大深度 递归写法
var maxDepth = function(root) {
if(!root) return 0
let depth = 0
for(let node of root.children) {
depth = Math.max(depth, maxDepth(node))
}
return depth + 1
}
// N叉树的最大深度 层序遍历
var maxDepth = function(root) {
if(!root) return 0
let count = 0
let queue = [root]
while(queue.length) {
let size = queue.length
count++
while(size--) {
let node = queue.shift()
for (let item of node.children) {
item && queue.push(item);
}
}
}
return count
};
111.二叉树的最小深度
力扣题目链接
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

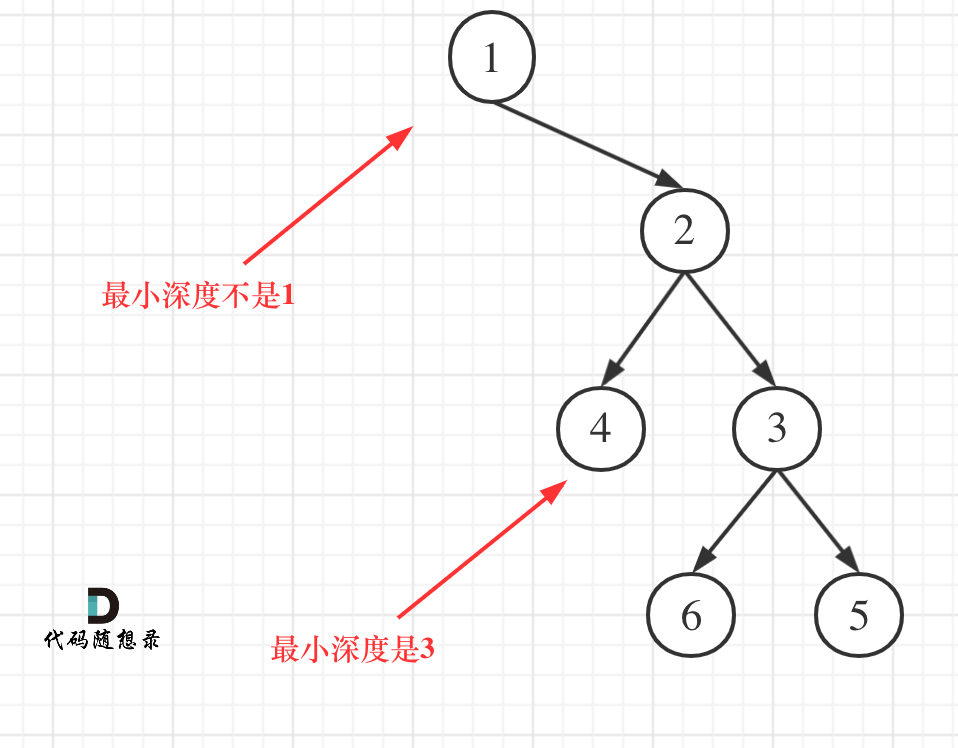
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。,注意是叶子节点。
什么是叶子节点,左右孩子都为空的节点才是叶子节点!
var minDepth=function(root){
if(root===null) return 0;
if(root.left===null&&root.right===null) return 1;
let min_depth=Number.MAX_SAFE_INTEGER;
if(root.left!==null){
min_depth=Math.min(minDepth(root.left),min_depth);
}
if(root.right!==null){
min_depth=Math.min(minDepth(root.right),min_depth);
}
return min_depth+1;
}#递归法
- 确定递归函数的参数和返回值 参数为要传入的二叉树根节点,返回的是int类型的深度。
- 确定终止条件 终止条件也是遇到空节点返回0,表示当前节点的高度为0。
- 确定单层递归的逻辑
var minDepth1 = function(root) {
if(!root) return 0;
// 到叶子节点 返回 1
if(!root.left && !root.right) return 1;
// 只有右节点时 递归右节点
if(!root.left) return 1 + minDepth(root.right);
// 只有左节点时 递归左节点
if(!root.right) return 1 + minDepth(root.left);
return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
};// 迭代法
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
if(!root) return 0;
const queue = [root];
let dep = 0;
// 队列不为空时
while(queue.length) {
let size = queue.length;
dep++;
while(size--){
const node = queue.shift();
// 到第一个叶子节点 返回 当前深度
if(!node.left && !node.right) return dep;
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
};222.完全二叉树的节点个数
力扣题目链接
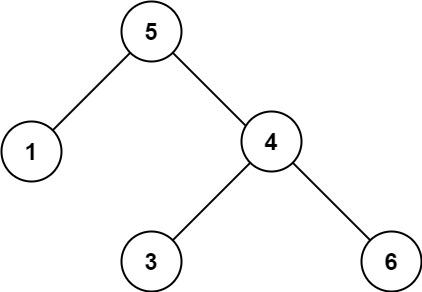
给出一个完全二叉树,求出该树的节点个数。
示例 1:
- 输入:root = [1,2,3,4,5,6]
- 输出:6
示例 2:
- 输入:root = []
- 输出:0
示例 3:
- 输入:root = [1]
- 输出:1
提示:
- 树中节点的数目范围是[0, 5 * 10^4]
- 0 <= Node.val <= 5 * 10^4
- 题目数据保证输入的树是 完全二叉树
#思路
var countNodes = function(root) {
if(root===null) return 0;
return 1+countNodes(root.left)+countNodes(root.right);
};
//代码随想录
// 递归版本
var countNodes = function(root) {
//递归法计算二叉树节点数
// 1. 确定递归函数参数
const getNodeSum = function(node) {
//2. 确定终止条件
if(node === null) {
return 0;
}
//3. 确定单层递归逻辑
let leftNum = getNodeSum(node.left);
let rightNum = getNodeSum(node.right);
return leftNum + rightNum + 1;
}
return getNodeSum(root);
};
// 迭代(层序遍历)版本
var countNodes = function(root) {
//层序遍历
let queue = [];
if(root === null) {
return 0;
}
queue.push(root);
let nodeNums = 0;
while(queue.length) {
let length = queue.length;
while(length--) {
let node = queue.shift();
nodeNums++;
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return nodeNums;
};
// 利用完全二叉树性质
var countNodes = function(root) {
//利用完全二叉树的特点
if(root === null) {
return 0;
}
let left = root.left;
let right = root.right;
let leftDepth = 0, rightDepth = 0;
while(left) {
left = left.left;
leftDepth++;
}
while(right) {
right = right.right;
rightDepth++;
}
if(leftDepth == rightDepth) {
return Math.pow(2, leftDepth+1) - 1;
}
return countNodes(root.left) + countNodes(root.right) + 1;
};