验证二叉搜索树

中等

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。

• 节点的右子树只包含 大于 当前节点的数。

• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]

输出：true

示例 2：

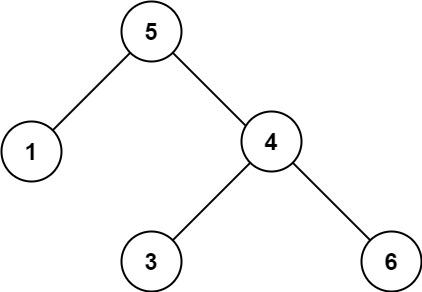
输入：root = [5,1,4,null,null,3,6]

输出：false

解释：根节点的值是 5 ，但是右子节点的值是 4 。

题解（中序遍历）

1. 创建节点和list集合，list集合用于节点遍历后值的存储

2. 声明一个中序遍历方法，递归求解

3. 传入参数，获取节点值

4. 遍历集合，根据中序遍历性质，如果找到前一个值大于后一个值，说明该树不符合平衡二叉树的特点，返回false,否则返回true。

中序遍历（左+中+右）

（当前节点左右子树不为空时递归调用）先递归遍历左子树节点，在获取当前节点，在递归遍历右子树节点

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        infixOrder(root,list);
        System.out.println(list);
        boolean flag = true;
        for (int i = 1; i < list.size(); i++) {
            if(list.get(i-1) >= list.get(i)){
                flag = false;
                System.out.println(flag);
                return flag;
            }
        }
        System.out.println(flag);
        return flag;
    }
    public void infixOrder(TreeNode root,List<Integer> list){
        if(root != null){
            if(root.left != null){
                infixOrder(root.left,list);
            }
            list.add(root.val);
            if(root.right != null){
                infixOrder(root.right,list);
            }
        }
    }
}