1、分位数

1.1、分位数的概念

分位数（Quantile），亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位数、百分位数等。分位数指的就是连续分布函数中的一个点，这个点对应概率p。若概率0<p<1，随机变量X或它的概率分布的分位数Za，是指满足条件p(X≤Za)=α的实数
通俗的分位数的概念就是将数据从小到大排序后，处于某个位置的数。

1.2、特殊分位数

• 第一四分位数(Q1)，又称“较小四分位数”、上四分位数。等于该样本中所有数值由小到大排列后第25%的数字；
• 第二四分位数(Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字；
• 第三四分位数(Q3)，又称“较大四分位数”、下四分位数。等于该样本中所有数值由小到大排列后第75%的数字。
• 第三四分位数与第一四分位数的差距又称四分位距（interquartile range, IQR）。IQR = Q3 − Q1。

1.3、分位数的计算

例如：有如下12个数，求Q1，Q2，Q3以及9分位数。

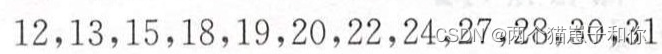
解：数据按照从小到大排序
第一分位数=Q1：i=np=120.25=3,Q1=(位置3的数据+位置4的数据)/2=(15+18)/2=16.5
第二分位数=Q2：i=np=120.5=6,Q2=(位置6的数据+位置7的数据)/2=(20+22)/2=21
第三分位数=Q3：i=np=120.75=9,Q2=(位置9的数据+位置10的数据)/2=(27+28)/2=27.5
9分位数：i=np=120.9=10.8,9分位数=位置11的数据=30

2、箱线图

2.1、概念

箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比较。箱形图于1977年由美国著名统计学家约翰·图基（John Tukey）发明。它能显示出一组数据的最大值、最小值、中位数、及上下四分位数。

箱形图提供了一种只用5个点对数据集做简单总结的方式。这5个点包括中点、Q1、Q3、分部状态的高位和低位。箱形图很形象的分为中心、延伸以及分布状态的全部范围。

2.2、作图步骤

1. 获取异常值。认为在Q3+1.5IQR~Q1-1.5IQR之间的数据为正常值，其他的为异常值；
2. 求最大值，最小值，第一分位数，第二分位数（中位数），第三分位数；
3. 画数轴，度量单位大小和数据批的单位一致，起点比最小值稍小，长度比该数据批的全距稍长；
4. 画一个矩形盒，两端边的位置分别对应数据批的上下四分位数（Q3和Q1）。在矩形盒内部中位数（Xm）位置画一条线段为中位线。
5. 在Q3+1.5IQR和Q1－1.5IQR处画两条与中位线一样的线段，这两条线段为异常值截断点，称其为内限；在Q3+3IQR和Q1－3IQR处画两条线段，称其为外限。处于内限以外位置的点表示的数据都是异常值，其中在内限与外限之间的异常值为温和的异常值（mild outliers），在外限以外的为极端的异常值(extreme outliers)。四分位距IQR=Q3-Q1；
6. 从矩形盒两端边向外各画一条线段直到不是异常值的最远点，表示该批数据正常值的分布区间；
7. 用“〇”标出温和的异常值，用“*”标出极端的异常值。相同值的数据点并列标出在同一数据线位置上，不同值的数据点标在不同数据线位置上。至此一批数据的箱形图便绘出了。统计软件绘制的箱形图一般没有标出内限和外限。
   

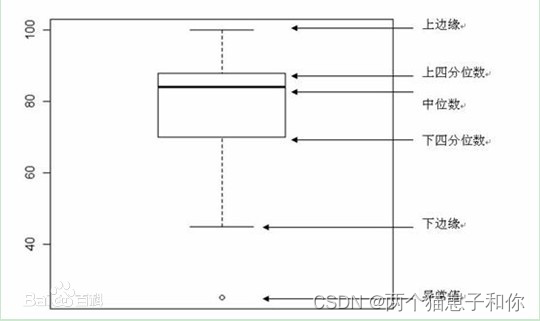
2.3、箱线图的作用

2.3.1、定位异常值

一批数据中的异常值值得关注，忽视异常值的存在是十分危险的，不加剔除地把异常值包括进数据的计算分析过程中，对结果会带来不良影响；重视异常值的出现，分析其产生的原因，常常成为发现问题进而改进决策的契机。箱形图为我们提供了识别异常值的一个标准：异常值被定义为小于Q1－1.5IQR或大于Q3+1.5IQR的值。虽然这种标准有点任意性，但它来源于经验判断，经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知，基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的，而均值和标准差的耐抗性极小，异常值本身会对它们产生较大影响，这样产生的异常值个数不会多于总数0.7%。显然，应用这种方法于非正态分布数据中判断异常值，其有效性是有限的。箱形图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，它只是真实直观地表现数据形状的本来面貌；另一方面，箱形图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响，箱形图识别异常值的结果比较客观。由此可见，箱形图在识别异常值方面有一定的优越性。

2.3.2、偏态和尾重

比较标准正态分布、不同自由度的t分布和非对称分布数据的箱形图的特征，可以发现：对于标准正态分布的大样本，只有 0.7%的值是异常值,中位数位于上下四分位数的中央,箱形图的方盒关于中位线对称。选取不同自由度的t分布的大样本，代表对称重尾分布，当t分布的自由度越小，尾部越重，就有越大的概率观察到异常值。以卡方分布作为非对称分布的例子进行分析，发现当卡方分布的自由度越小，异常值出现于一侧的概率越大，中位数也越偏离上下四分位数的中心位置，分布偏态性越强。异常值集中在较大值一侧，则分布呈现右偏态；；异常值集中在较小值一侧，则分布呈现左偏态。这个规律揭示了数据批分布偏态和尾重的部分信息，尽管它们不能给出偏态和尾重程度的精确度量，但可作为我们粗略估计的依据。

2.3.3、数据的形状

同一数轴上，几批数据的箱形图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便一目了然。在一批数据中，哪几个数据点出类拔萃，哪些数据点表现不及一般，这些数据点放在同类其它群体中处于什么位置，可以通过比较各箱形图的异常值看出。各批数据的四分位距大小，正常值的分布是集中还是分散，观察各方盒和线段的长短便可明了。每批数据分布的偏态如何，分析中位线和异常值的位置也可估计出来。还有一些箱形图的变种，使数据批间的比较更加直观明白。例如有一种可变宽度的箱形图，使箱的宽度正比于批量的平方根，从而使批量大的数据批有面积大的箱，面积大的箱有适当的视觉效果。如果对同类群体的几批数据的箱形图进行比较，分析评价，便是常模参照解释方法的可视图示；如果把受测者数据批的箱形图与外在效标数据批的箱形图比较分析，便是效标参照解释的可视图示。箱形图结合这些分析方法用于质量管理、人事测评、探索性数据分析等统计分析活动中去，有助于分析过程的简便快捷，其作用显而易见。