摘要

　　虽然相位感知语音处理近年来受到越来越多的关注，但大多数帧长约为32 ms的窄带STFT方法显示出相位对整体性能的影响相当有限。与此同时，现代基于深度神经网络(DNN)的方法，如Conv-TasNet，隐式修改幅度和相位，在非常短的帧(2 ms)上产生了出色的性能。

　　在这一观察的启发下，本文系统地研究了相位和幅度在不同帧长的DNN语音增强中的作用。结果表明，基于相位感知的神经网络可以充分利用之前关于纯净语音重建的研究表明：当使用短帧时，相位谱变得更加重要，而幅度谱的重要性降低。实验表明，当同时估计幅度和相位时，较短的帧可以显著提高具有显式相位估计的DNN的性能。相反，如果只处理幅值不估计相位，32 ms帧可以获得最佳性能。基于DNN的相位估计得益于使用较短的帧，并建议基于神经网络的相位感知语音增强方法推荐用约4 ms的帧长。

索引术语：语音增强，神经网络，帧长，相位感知

1 引言

　　单通道语音增强通常在时频域进行，为了获得时频表示，可以应用诸如短时傅里叶变换(STFT)等具有多个自由参数的变换。这些参数(即帧长、帧移和窗函数，参见第2节)必须适当地选择。然而，不仅要考虑信号本身，还要考虑应用于时频表示的算法；STFT参数的选择应该产生对当前算法最有用的表示[1]。

　　本文重点关注基于深度神经网络(DNNs)的语音增强算法帧长的选择，特别是针对相位感知方法。STFT表示是复数的，通常分为幅度谱和相位谱。相位谱与语音增强任务的相关性一直是一个争论的话题。传统上，由于经验研究[2]和理论结果[3]，它被认为是不重要的。然而，最近的研究表明，相位确实携带语音相关信息[4]、[5]。受这些研究结果的推动，相位感知语音处理得到了一定程度的复兴，并提出了多种相位感知语音处理方法，如[6]-[10]。

　　近年来，深度神经网络已迅速成为许多领域的首选工具，包括音频和语音处理。因此，最近的许多相位感知的语音增强和声源分离方法使用深度神经网络直接估计相位谱[11]-[13]，或估计相位导数并从中重建相位[14]，[15]。其他基于DNN的方法包括直接对复数谱进行操作，而不将[16]-[18]分为幅度和相位，或者仅考虑相位以改进幅度估计[19]。

　　一些作者采取了不同的方法，完全用学习到的编码器-解码器机制取代了基于STFT的表示，这通常会产生实数表示[20]-[22]。这些编码器-解码器方法一个有趣方面是，当使用大约2ms的非常短的帧时，它们表现出非常好的性能，甚至短至0.125毫秒[21]。这与基于STFT的方法形成了鲜明的对比，后者通常使用大约20 ms到60 ms的帧长。注意，虽然学习的编码器-解码器方法最初是为了源分离而提出的，但它们在语音增强任务[23]，[24]上也表现出良好的性能。

　　随着开创性的学习编码器-解码器Conv-TasNet模型[20]的发布，一些作者提出了扩展和分析。在其他结果中，已经表明，ConvTasNet性能的主要影响因素是使用短帧和时域损失函数，而不是学习的编码器-解码器[25]，[26]。研究还表明，当用STFT替换学习到的编码器时，最佳输入特征集取决于所选择的帧长[26]，[27]；对于较长的帧(25 ms到64 ms)，幅度谱工作得很好，而较短的帧(2 ms到4 ms)只有将完整的复数谱作为输入(以实部和虚部连接的形式)时才表现出更好的性能。这个观察是特别重要的，因为它意味着相位感知语音处理(无论是隐式还是显式相位估计)应该可能采用与仅幅值处理不同的帧长。

　　论文[24]虽然已经研究了相位感知语音增强DNNs中损失函数的选择对于感知测量的影响，但我们还不知道关于帧长选择的这种分析。先前与DNN无关的研究表明，相位对语音相关任务的重要性随着STFT参数的选择而变化。特别是，在不使用典型帧长(对应于大约20 ms到40 ms)，使用更短帧[28]，[29]或使用有效缩短帧[4]，可以仅从相位谱中获得非常好的信号重建。对于较长的典型帧[28]、[30]，也观察到了类似的结果。然而，由于长帧会产生算法延迟，这对于许多实时语音处理设备来说可能是禁止的，因此出于实际原因，我们选择关注短帧。从[28]复制的图1显示了相位和幅度对重建纯净语音可懂度的贡献如何随着帧长的变化而变化。人们观察到，随着帧变短，相位变得更重要，而幅度逐渐失去相关性。然而，请注意，这些发现是基于oracle数据上的一些人工信号重构实验——它们是否也适用于实际的语音增强、源分离等尚不清楚。

图1：从[28]复制的结果摘录，这里显示为说明目的。

从幅度谱或相位谱重构语音(用噪声代替其他分量)时，得到的语音信号的可懂度很大程度上取决于帧长的选择。完整图及详细信息见[28，图2]。

　　语音处理中典型的帧长(约32 ms)可以被认为是准平稳的，但又足够长，可以覆盖多个浊音的基本周期(基本周期在2 ms到12.5 ms之间)[31]。这些考虑适用于幅度谱，但不一定适用于相位谱。事实上，似乎相位谱的不相关性部分是由于实验中帧长的选择。

　　基于之前的结果和观察，本文试图回答的问题是：哪种帧长对基于STFT的相位感知语音增强DNN最有利？以具有显式相位估计的深度神经网络为例，分析和比较了不同帧长下的性能。为了获得进一步的见解，本文还试图描述每个帧长上的幅度和相位谱的相对贡献，并表明上述关于短帧中相位重要性的观察在语音增强的背景下也是相关和有用的。

2 预备知识

　　将时域信号$x(n)$分割为长度为$M$、位移为$H$的重叠帧，计算其STFT，对每一帧应用窗函数$w(n)$，然后对其进行离散傅里叶变换(DFT)，将其转换到频域。假设采用单边$M$点DFT，得到复数谱$x\in C^{K*L}$，定义为

$$公式1：X_{k,l}=\sum_{n=0}^{M-1}x(lH+n)w(n)e^{-j2\pi \frac{kn}{M}}$$

其中$k$是频率索引，$l$是帧索引，$K=\frac{M}{2}+1$是频点的数量，$L$是时间帧的数量。除非另有说明，否则我们总是考虑整个频谱，因此忽略下面的索引。为了方便起见，我们还定义了重叠率$R=\frac{M-H}{M}$。由于$M$是单个帧中的样本数量，我们定义$M_t=\frac{M}{f_s}$(其中$f_s$是采样频率)为物理帧长度(以秒为单位)。从这一点开始，术语帧长度将指的是$M_t$。

　　复数谱在极坐标下可以表示为幅度谱$|X|$和相位谱$\phi X$：

$$公式2：X=|X|e^{j\phi X}$$

在语音增强的背景下，我们考虑了一个加性噪声模型

$$公式3：X=S+V$$

其中$S$和$V$分别是纯净语音信号和加性噪声分量。给定噪声信号$X$，任务是计算估计$\hat{S}=|\hat{S}|e^{j\hat{\phi }S}$，随后将其转换回时域，得到估计的干净信号$\hat{s}$。

3 神经网络框架

　　本文提出的DNN架构是[12]中提出的用于视听语音分离和增强的模型的改编，由耦合的幅值和相位子网络组成。虽然我们在这里不考虑音视频输入，但该模型相对简单，可以对幅度和相位进行显式估计，这对我们的实验至关重要。与视频流相关的部分被忽略，模型进行了相应的调整。结果网络如图2所示，如下所述

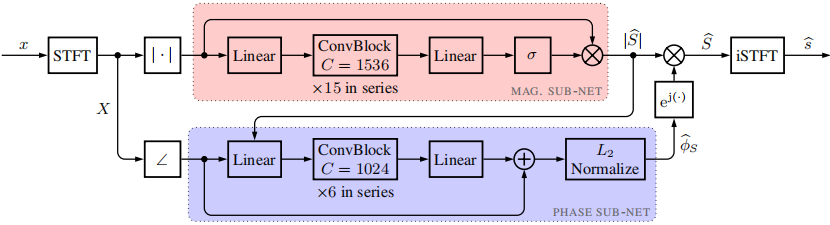
图2：所提出的网络架构概述，基于[12]的视听模型，尽管仅使用带噪语音信号作为输入

基本卷积块如图3所示。请注意，相位子网络的输入由估计幅度以及噪声相位的余弦和正弦组成，为了简单起见，这里显示为单个输入

　　这两个子网络都使用沿时间轴的一维深度可分离卷积层[32]实现卷积神经网络(在这种设置中，输入端的不同频点被视为通道)。两个网络都由多个相同的残差块组成；基本构建块由预激活(ReLU)、批量归一化层和卷积层组成，卷积层的输出被添加到块的输入中(见图3)。

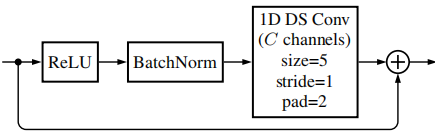
图3 基本残差卷积块，由ReLU预激活、批量归一化层和一维深度可分离卷积层组成

3.1 幅度子网络

　　幅度子网络采用带噪幅度谱$|X|$输出一个实数掩模，该掩模应用于带噪STFT幅度谱以产生幅度估计(注意，来自[12]的原始网络使用梅尔尺度的频谱以及视频特征作为输入)。噪声幅度谱通过15个卷积块的链进行，每个卷积块有1536个输入/输出通道。输入和输出的线性层有助于对频率间关系建模，并将数据投影到正确的维度。将sigmoid激活函数应用于输出，得到一个值在[0,1]内的实数掩码。实数的掩模与输入相乘，得到一个幅度估计$|\hat{S}|$。

3.2 相位子网络

　　相位子网络的输入是沿频率轴的$|\hat{S}|$， $cos(\phi X)$和$sin(\phi X)$的级联。它被输入到一个线性输入层，随后通过6个具有1024个通道的卷积块和一个线性输出层。线性层的输出被视为相位残差的余弦和正弦的级联，它们被添加到各自的输入。对得到的估计进行$L_2$归一化，以确保余弦和正弦输出彼此一致(即它们表示复平面上的一个单位向量)。

3.3 训练过程

　　与[12]中提出的多阶段学习方法相比，我们只是在由不同信噪比(SNR)的带噪和纯净语音样本对组成的整个训练集上训练网络(更多细节请参见第4.1节)。本文采用了一种时域损失函数，即负尺度不变信号失真比(negative scale invariant signal to distortion ratio, SI-SDR)[33]，而不是[12]中提出的频域损失函数。当幅度谱和相位谱都被估计时，SISDR损失已经被证明可以产生优越的结果[26]。

4 实验

　　我们进行的主要实验是比较该模型在不同STFT帧长$M$的性能，在感知和客观测量方面。由于我们考虑的模型包括相位和幅度的显式估计，我们还能够分析和量化幅度和相位估计的相对贡献，再次作为帧长的函数。这种分析的方式与[4]、[28]、[29]中的感知实验类似，尽管这里我们使用纯净语音幅度和相位的估计，而不是纯净或噪声时域信号。对于每个帧长，我们产生三个纯净语音信号的估计：网络的实际输出以及两个由估计幅度和噪声相位组成的合成信号，反之亦然：

$$公式4：\hat{s} =iSTFT\{|\widehat{S}| \mathrm{e}^{\mathrm{j} \widehat{\phi}_S}\}$$

$$公式5：\widehat{s}_{\mathrm{mag}} =iSTFT\{|\widehat{S}| \mathrm{e}^{\mathrm{j} \phi_X}\}$$

$$公式6：\widehat{s}_{\mathrm{ph}} =iSTFT\{|X| \mathrm{e}^{\mathrm{j} \widehat{\phi}_S}\}$$

　　为了进行公平的比较，我们必须保持DNN参数的数量恒定。在我们考虑的网络架构的情况下，参数的数量取决于频点数量$K$。因此，我们在应用DFT之前对帧进行零补全，使得K = 257，这对应于$f_s$ = 16kHz时我们考虑的最长帧($M_t$ = 32 ms)。在所有实验中，我们使用平方根Hann窗，重叠比R = 50%。同样的窗口用于正向和逆STFT。

4.1 数据及训练明细

　　在训练中，我们使用2020年深度噪声抑制(DNS)数据集[34]的纯净语音和噪声，SNR$\in ${- 5,0，…, 10} dB。每个语音长度为2 s，数据集总共包含100 h的语音，其中80%用于训练，剩余20%用于验证。使用Adam优化器训练所有模型，batch size大小为32，学习率为$10^{-4}$。如果10个迭代周期内验证损失没有减少，则停止训练。

　　在两个测试集上进行评估：DNS合成无混响测试集，包含150个节选语音，每个语音10 s，信噪比$\in ${0,1，…， 20}dB，另一个自定义测试集，由来自WSJ语料库[35]的纯净语音和来自CHiME3数据集[36]的噪声组成，混合信噪比$\in ${−10，−5，…, 20} dB。该测试集共包含672个摘要。所有训练和评估数据都以$f_s$ = 16kHz采样。

5 结果和讨论

表1：DNS测试集上的评估结果

对于每个重构信号(如公式(4)到(6)展示了各种帧长下POLQA和ESTOI的改进(对带噪输入信号的w.r.t.)

每列中最好的结果和接近的秒数以粗体显示

　　在DNS测试集上的评估结果如表1所示。虽然可理解性(在ESTOI方面)受帧长选择的影响不大，但我们看到了对语音质量(POLQA)的显著影响，它受益于减少帧长，直到在$M_t$ = 4 ms达到最大值，之后开始下降，但对于1 ms到2 ms的非常短的帧仍然达到相对较高的值。对于POLQA和ESTOI，基于幅度和基于相位的估计(分别为$\hat{s}_{mag}$和$\hat{s}_{ph}$)显示了一幅有趣的图像：在$M_t$ = 32 ms时，$\hat{s}_{mag}$达到了与$\hat{s}$相似的值，而基于相位的估计$\hat{s}_{ph}$与噪声输入相比几乎没有改善。随着帧长的减少，这种情况逐渐发生变化：基于幅度的估计失去了质量和可理解性，而基于相位的估计则相反。

图4：WSJ/CHiME测试集的评估结果(见章节4.1)。

图中显示了POLQA, ESTOI和SI-SDR在所有信噪比下的平均改进随帧长的变化。

误差带表示95%的置信区间。短帧有利于POLQA测量的语音估计质量。

此外，基于相位和基于幅度的重建的不同度量显示出一种互补的行为，这让人想起在之前的oracle实验中观察到的行为(参见图1)。

　　如图4所示，对更大的WSJ/CHiME数据集的评估在POLQA、ESTOI和SI-SDR方面显示出类似的趋势。虽然ESTOI和SI-SDR在帧长上几乎保持不变，但POLQA显然从较短的帧中受益。同样，可以看到基于幅度和基于相位的估计的互补行为。这种行为非常类似于早期基于oracle的研究[28]，[29]。实际上，∆ESTOI结果与图1之间有惊人的相似之处，尽管基于相位的估计变得更好的点略有偏移。

　　POLQA的改进在Mt = 4 ms时达到最大，其中基于相位的估计也达到最大。当帧数更短时，所有三个指标的性能都会下降。总的来说，ESTOI和SI-SDR的改进似乎并不强烈依赖于帧长，尽管上述互补行为也可以清楚地观察到。然而，在这种相位感知设置中，随着帧变短，语音质量(POLQA)确实呈现上升趋势。我们将这种依赖性归因于相位和幅度谱的相对贡献以及它们之间的相互作用。虽然基于幅值的估计显示短帧的质量下降，但相位谱的贡献提高了整体性能，导致了优越的结果。

　　由于图4中的结果是在所有信噪比下的平均结果，我们在图5中通过显示两个选定帧长(4 ms, 16 ms)在不同信噪比下的POLQA改进来提供进一步的了解。除了较短帧的整体性能较好和较长帧的相位估计不重要之外(cf. Fig. 4)，基于幅度和相位估计的质量对信噪比的依赖性更强。特别是，在低信噪比(≤0 dB)下，基于相位的估计实际上超过了基于幅度的估计，这表明相位估计在困难的噪声条件下尤其有益，根据先前的感知研究[37]。这也转化为联合估计的情况(即$\hat{s}$)，其中帧长之的∆POLQA差异在低信噪比下更明显。

图5：M_t$\in ${4,16}ms WSJ/CHiME测试集上的平均POLQA改进，显示为输入信噪比的函数

6 结论

在这项工作中，我们提出了一项关于帧长对基于DNNs的STFT相位感知语音增强的影响的研究。结果表明，通过使用相对较短的帧(4 ms)，与通常在基于STFT的处理中使用的较长帧相比，性能有了显著提高。此外，通过显式估计相位和幅度，我们能够表明这种性能提升与幅度和相位估计的单独贡献有关，这高度依赖于帧长。这反映了以前在oracle数据上的实验得出的见解，同时首次表明，可以利用这一现象来改善语音增强结果。

7 贡献

这项工作得到了德意志Forschungsgemeinschaft (DFG，德国研究基金会)的资助-项目编号247465126。我们要感谢J. Berger和Rohde&Schwarz swiss squal AG对POLQA的支持。

8 参考文献

[1] T. Virtanen, E. Vincent, and S. Gannot, “Time-Frequency Processing： Spectral Properties,” in Audio Source Separation and Speech Enhancement, John Wiley & Sons, Ltd, 2018, pp. 15–29.

[2] D. Wang and J. Lim, “The unimportance of phase in speech enhancement,” IEEE Trans. on Acoustics, Speech, and Signal Processing, vol. 30, no. 4, pp. 679–681, Aug. 1982. ∆POLQA ∆ESTOI ∆SI-SDR (dB) ∆POLQA

[3] Y. Ephraim and D. Malah, “Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator,” IEEE Trans. on Acoustics, Speech, and Signal Processing, vol. 32, no. 6, pp. 1109–1121, Dec. 1984.

[4] K. Paliwal, K. W´ojcicki, and B. Shannon, “The importance of phase in speech enhancement,” Speech Communication, vol. 53, no. 4, pp. 465–494, Apr. 2011.

[5] T. Gerkmann, M. Krawczyk-Becker, and J. Le Roux, “Phase Processing for Single-Channel Speech Enhancement： History and recent advances,” IEEE Signal Processing Magazine, vol. 32, no. 2, pp. 55–66, Mar. 2015.

[6] J. Le Roux and E. Vincent, “Consistent Wiener Filtering for Audio Source Separation,” IEEE Signal Processing Letters, vol. 20, no. 3, pp. 217–220, Mar. 2013.

[7] T. Gerkmann, “MMSE-optimal enhancement of complex speech coefficients with uncertain prior knowledge of the clean speech phase,” in 2014 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), May 2014.

[8] ——, “Bayesian Estimation of Clean Speech Spectral Coeffi- cients Given a Priori Knowledge of the Phase,” IEEE Trans. Signal Process., vol. 62, no. 16, pp. 4199–4208, Aug. 2014.

[9] M. Krawczyk and T. Gerkmann, “STFT Phase Reconstruction in Voiced Speech for an Improved Single-Channel Speech Enhancement,” IEEE/ACM Trans. Audio Speech Lang. Process., vol. 22, no. 12, pp. 1931–1940, Dec. 2014.

[10] P. Mowlaee and J. Kulmer, “Harmonic Phase Estimation in Single-Channel Speech Enhancement Using Phase Decomposition and SNR Information,” IEEE/ACM Trans. on Audio, Speech, and Language Processing, vol. 23, no. 9, pp. 1521–1532, Sep. 2015.

[11] N. Takahashi, P. Agrawal, N. Goswami, and Y. Mitsufuji, “PhaseNet： Discretized Phase Modeling with Deep Neural Networks for Audio Source Separation,” in Interspeech 2018, Sep. 2, 2018.

[12] T. Afouras, J. S. Chung, and A. Zisserman, “The Conversation： Deep Audio-Visual Speech Enhancement,” in Interspeech 2018, Sep. 2, 2018.

[13] J. Le Roux, G. Wichern, S. Watanabe, A. Sarroff, and J. R. Hershey, “Phasebook and Friends： Leveraging Discrete Representations for Source Separation,” IEEE Journal of Selected Topics in Signal Processing, vol. 13, no. 2, pp. 370–382, May 2019.

[14] N. Zheng and X.-L. Zhang, “Phase-Aware Speech Enhancement Based on Deep Neural Networks,” IEEE/ACM Trans. on Audio, Speech, and Language Processing, vol. 27, no. 1, pp. 63–76, Jan. 2019.

[15] Y. Masuyama, K. Yatabe, Y. Koizumi, Y. Oikawa, and N. Harada, “Phase Reconstruction Based On Recurrent Phase Unwrapping With Deep Neural Networks,” in 2020 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), May 2020.

[16] D. S. Williamson, Y. Wang, and D. Wang, “Complex ratio masking for joint enhancement of magnitude and phase,” in 2016 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), Mar. 2016.

[17] K. Tan and D. Wang, “Learning Complex Spectral Mapping With Gated Convolutional Recurrent Networks for Monaural Speech Enhancement,” IEEE/ACM Trans. on Audio, Speech, and Language Processing, vol. 28, pp. 380–390, 2020.

[18] Y. Hu, Y. Liu, S. Lv, M. Xing, S. Zhang, Y. Fu, J. Wu, B. Zhang, and L. Xie, “DCCRN： Deep Complex Convolution Recurrent Network for Phase-Aware Speech Enhancement,” in Interspeech 2020, Oct. 25, 2020.

[19] H. Erdogan, J. R. Hershey, S. Watanabe, and J. Le Roux, “Phasesensitive and recognition-boosted speech separation using deep recurrent neural networks,” in 2015 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), Apr. 2015.

[20] Y. Luo and N. Mesgarani, “Conv-TasNet： Surpassing Ideal Time–Frequency Magnitude Masking for Speech Separation,” IEEE/ACM Trans. on Audio, Speech, and Language Processing, vol. 27, no. 8, pp. 1256–1266, Aug. 2019.

[21] Y. Luo, Z. Chen, and T. Yoshioka, “Dual-Path Rnn： Efficient Long Sequence Modeling for Time-Domain Single-Channel Speech Separation,” in 2020 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), May 2020.

[22] C. Subakan, M. Ravanelli, S. Cornell, M. Bronzi, and J. Zhong, “Attention Is All You Need In Speech Separation,” in 2021 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), Jun. 2021.

[23] Y. Koyama, T. Vuong, S. Uhlich, and B. Raj, “Exploring the Best Loss Function for DNN-Based Low-latency Speech Enhancement with Temporal Convolutional Networks,” Aug. 20, 2020. arXiv： 2005.11611 [cs, eess].

[24] Z.-Q. Wang, G. Wichern, and J. Le Roux, “On the Compensation Between Magnitude and Phase in Speech Separation,” IEEE Signal Processing Letters, vol. 28, pp. 2018–2022, 2021.

[25] D. Ditter and T. Gerkmann, “A Multi-Phase Gammatone Filterbank for Speech Separation Via Tasnet,” in 2020 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), May 2020.

[26] J. Heitkaemper, D. Jakobeit, C. Boeddeker, L. Drude, and R. Haeb-Umbach, “Demystifying TasNet： A Dissecting Approach,” in 2020 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), May 2020.

[27] M. Pariente, S. Cornell, A. Deleforge, and E. Vincent, “Filterbank Design for End-to-end Speech Separation,” in 2020 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), May 2020.

[28] M. Kazama, S. Gotoh, M. Tohyama, and T. Houtgast, “On the significance of phase in the short term Fourier spectrum for speech intelligibility,” The Journal of the Acoustical Society of America, vol. 127, no. 3, pp. 1432–1439, 2010.

[29] T. Peer and T. Gerkmann, “Intelligibility Prediction of Speech Reconstructed From Its Magnitude or Phase,” in Speech Communication; 14th ITG Conference, Kiel (online), Sep. 2021.

[30] L. Alsteris and K. Paliwal, “Importance of window shape for phase-only reconstruction of speech,” in 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, vol. 1, May 2004.

[31] K. K. Paliwal, J. G. Lyons, and K. K. W´ojcicki, “Preference for 20-40 ms window duration in speech analysis,” in 2010 4th International Conference on Signal Processing and Communication Systems, 2010.

[32] F. Chollet, “Xception： Deep Learning with Depthwise Separable Convolutions,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, Jul. 2017.

[33] J. Le Roux, S. Wisdom, H. Erdogan, and J. R. Hershey, “SDR – Half-baked or Well Done?” In 2019 IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), May 2019.

[34] C. K. Reddy, V. Gopal, R. Cutler, E. Beyrami, R. Cheng, H. Dubey, S. Matusevych, R. Aichner, A. Aazami, S. Braun, P. Rana, S. Srinivasan, and J. Gehrke, “The INTERSPEECH 2020 Deep Noise Suppression Challenge： Datasets, Subjective Testing Framework, and Challenge Results,” in Interspeech 2020, Oct. 25, 2020.

[35] D. B. Paul and J. M. Baker, “The design for the wall street journal-based CSR corpus,” in Proceedings of the Workshop on Speech and Natural Language - HLT ’91, Harriman, New York, 1992.

[36] J. Barker, R. Marxer, E. Vincent, and S. Watanabe, “The third ‘CHiME’ speech separation and recognition challenge： Dataset, task and baselines,” in 2015 IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), 2015.

[37] M. Krawczyk-Becker and T. Gerkmann, “An evaluation of the perceptual quality of phase-aware single-channel speech enhancement,” The Journal of the Acoustical Society of America, vol. 140, no. 4, EL364–EL369, Oct. 2016.