2021网络空间安全西湖学术论坛线上报告中介绍了差分隐私过去发展，目前现状以及未来研究方向。博主对这个报告进行了介绍与总结。总结中提到学习差分隐私最重要的环节是：

1. 了解差分隐私的基本机制：拉普拉斯机制、指数机制和高斯机制
2. 差分隐私的组合定理与一些性质
3. 差分隐私的数学证明
   本笔记按照这个思路进行学习。

拉普拉斯机制

拉普拉斯机制针对数值型查询进行隐私保护。即针对$f:D\to R^d$的情况。其实现为$M(D)$：
$$M(D)=f(D)+(Y_1,Y_2,...Y_d)$$即在数据的查询结果$f(D)$上添加服从拉普拉斯分布的噪声，从而做到保护数据的目的。
其中$Y_i\sim Lap(\Delta /ϵ)$，$\Delta$是全局敏感度。

使用拉普拉斯机制对数据进行保护满足$ϵ$差分隐私，证明如下：
$$\begin{gathered} \frac{pr[M(D)=t]}{pr[M(D^{\prime })=t]}=\frac{pr[Y=t-h]}{pr[Y=t-h^{\prime }]} \\ =\frac{\frac{1}{2\lambda }\exp (-\frac{|t-h|}{\lambda })}{\frac{1}{2\lambda }\exp (-\frac{|t-h^{\prime }|}{\lambda })} \\ =\exp (\frac{|t-h^{\prime }|}{\lambda }-\frac{|t-h^{\prime }|}{\lambda }) \\ \le \exp (\frac{|h-h^{\prime }|}{\lambda }) \\ =\exp (ϵ) \end{gathered}$$
证明思路为：

1. 将引入机制后的最终结果相等的概率比值按照拉普拉斯机制的定义转换成对噪声取值的要求
2. 将噪音的概率引入到计算公式中
3. 进行除法约分计算
4. 利用距离公式
5. 利用$\Delta$的定义进行化简

拉普拉斯分布

当随机变量$Y$满足其取值为$y$的概率为$$pr[Y=y]=\frac{1}{2\lambda }\exp (-\frac{|y-\mu |}{\lambda })$$
我们称随机变量$Y$服从拉普拉斯分布$Y\sim Lap(\lambda )$.

常见的$f$函数

对于关系数据R，常见的$f$函数包括：

1. 计数
2. 均值
3. 中位数
4. 直方图

有关$\Delta$

对于不同的$f$，$\Delta$的取值不尽相同，例如对于计数函数，$\Delta =1$；对于直方图函数，$\Delta =2$.

指数机制

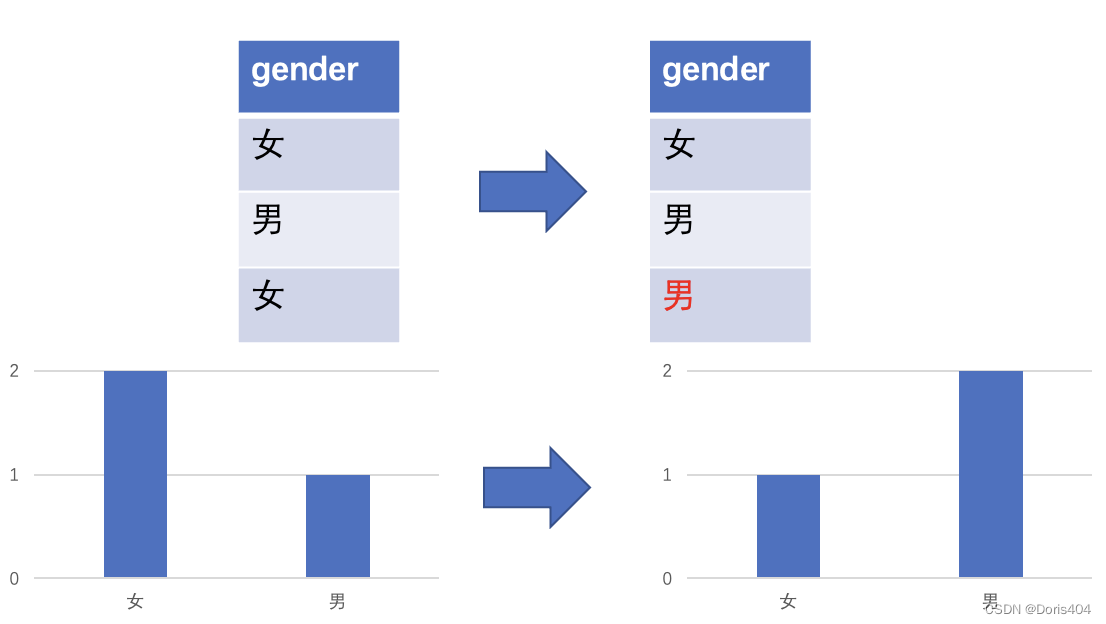
指数机制针对非数值查询进行隐私保护，这与拉普拉斯针对数值型查询进行隐私保护有着巨大的不同。以为数字产品做定价这个场景为例，假定存在$n=3$个买者，每个买者对于商品有自己的定价，定价分别为$(1,1,3.01)$,在这个设定下，当价格从1增加到1.1时，1号和2号买方不买，只有3号买方买，则总收益从3突然减小到1.01。在这个例子中我们知道价格的轻微变化会导致收益的剧烈变化。

考虑数据集$D\in x^n$（可以理解为上述情景中每个用户的定价）给定范围$R$（上述例子中定价的范围）效用函数$\mu$（最终收益），指数机制保证以正比于$\exp (\frac{ϵ\mu (D,R)}{2{\Delta }_{\mu }})$的概率得到$r$.即$$pr[M_E(x)=r]=\frac{\exp (ϵ\mu (x,r)/2{\Delta }_{\mu })}{{\sum }_{r^{\prime }\in R}\exp (ϵ\mu (x,r^{\prime })/2{\Delta }_{\mu })}$$

$M_E$满足$ϵ$差分隐私，其证明如下：$$\frac{pr[M_E(x)=r]}{pr[M_E(x^{\prime })=r]}=\frac{\exp (ϵ\mu (x,r)/2{\Delta }_{\mu })}{\exp (ϵ\mu (x^{\prime },r)/2{\Delta }_{\mu })}=\exp (\frac{ϵ(\mu (x,r)-\mu (x^{\prime },r))}{2{\Delta }_{\mu }})\le \exp (\frac{ϵ\times 2{\Delta }_{\mu }}{2{\Delta }_{\mu }})=\exp (ϵ)$$

有关${\Delta }_{\mu }$

${\Delta }_{\mu }$衡量了效用函数的敏感度，其定义为$${\Delta }_{\mu }=\underset{r\in R}{\max }\underset{x,x^{\prime }arenbrs}{\max }|\mu (x,r)-\mu (x^{\prime },r)|$$

一个例子：定价

数字产品定价场景中，假定产品的个数可以不受限制，整个市场有3个用户，每个用户对产品的心目定价为确定已知，用户1的定价为1，用户2的定价为1，用户3的定价为3.01，即用户定价向量为(1,1,3.01)，下面考虑定价对总收益的影响。在定价小于1时，随着价格的增加，收益会增加；价格超过1后用户1和2停止购买，总收益会突然减小，然后随着价格上涨，3号用户一个人贡献的总收益逐渐增加；最后当价格超过3号用户心中的价格3.01后，整个市场无人购买，总收益变成0。

性质

Utility

令$OPT(X)=ma{x}_{r\in R}\mu (x,r)$是最大效用函数，$R^{\ast }$是达到最大效用函数的目标集合，则有$$pr[\mu (M_E(x)\le OPT(X)-\frac{2{\Delta }_{\mu }}{ϵ}(\ln (\frac{|R|}{|R^{\ast }|})+t)]\le \exp (-t)$$其证明如下：$$pr[s(M_E(x)\le c]=\sum _{r:\mu (x,r)\le c}\frac{\exp (\frac{ϵ\mu (x,r)}{2{\Delta }_{\mu }})}{{\sum }_{r^{\prime }\in R}\exp (\frac{ϵ\mu (x,r^{\prime })}{2{\Delta }_{\mu }})}\le \frac{|R|}{|R^{\ast }|}\exp (\frac{ϵ}{2{\Delta }_{\mu }}(c-OPT(X)))$$为了找到上界，应该找到分子的上界和分母的下界，这里使用到效用函数的范围：对于分子而言效用函数小于等于$c$，因此分子中的效用函数可以被$c$限定住，求和则涉及到满足效用函数小于$c$的个数，其最大不会超过整个范围空间$R$，因此分子小于等于$|R|\exp (\frac{ϵc}{2{\Delta }_{\mu }})$；对于分母我们要找其大于什么，由效用函数的最大值为$OPT(X)$我们可以得到分母大于等于效用函数取值为$OPT(X)$的项之和，即分母大于等于$|R^{\ast }|\exp (\frac{ϵOPT(X)}{2{\Delta }_{\mu }})$.令$c=OPT(X)-\frac{2{\Delta }_{\mu }}{ϵ}(\ln (\frac{|R|}{|R^{\ast }|})+t)$则可以得证。

高斯机制

高斯机制与拉普拉斯机制类似，均通过在响应结果上加噪音达到隐私保护的效果，只不过与拉普拉斯机制不同，高斯机制加的噪音服从高斯分布。
$$M(D)=f(D)+(Y_1,Y_2,...Y_d)$$其中$Y_i\sim N(0,{\sigma }^2)$ ${\sigma }^2=(\frac{{\Delta }_2}{ϵ}\sqrt{\log (1/\lambda )}{)}^2$.

高斯机制无法确保$ϵ$差分隐私，而是退而求其次达到了$(ϵ,\delta )$差分隐私，这里的$\delta$是松弛项，表示隐私保护做得不好的范围。可以证明高斯机制实现了$(ϵ,\delta )$差分隐私，证明如下：

首先证明$L_{M(D)||M(D^{\prime })}\sim N(\frac{||f(D)-f(D^{\prime })|{|}_2^2}{2{\sigma }^2},\frac{||f(D)-f(D^{\prime })|{|}_2^2}{{\sigma }^2})$然后利用分布的特点，计算出$L_{M(D)||M(D^{\prime })}$小于$ϵ$的概率是$1-\delta$.

1. 证明$L_{M(D)||M(D^{\prime })}\sim N(\frac{||f(D)-f(D^{\prime })|{|}_2^2}{2{\sigma }^2},\frac{||f(D)-f(D^{\prime })|{|}_2^2}{{\sigma }^2})$
   令$f(x)-f(x^{\prime })=v$，则有$$\begin{gathered} L_{M(D)||M(D^{\prime })}=\ln (\frac{pr[M(D)=f(D)+x]}{pr[M(D^{\prime })=f(D)+x]}) \\ =\ln (\frac{\exp (-||x|{|}_2^2/2{\delta }^2)}{\exp (-||x+v|{|}_2^2/2{\delta }^2)}) \\ =\frac{1}{2{\sigma }^2}(||x+v|{|}_2^2-||x|{|}_2^2) \\ =\frac{1}{2{\sigma }^2}(\sum _i^k(v_i^2+2x_i{v}_i)) \end{gathered}$$可以发现$L_{M(D)||M(D^{\prime })}$的计算结果中$x_i$服从正态分布，$v_i$是$v$的分量。由于正态分布满足线性关系，可以知道$L_{M(D)||M(D^{\prime })}$服从正态分布，并且其均值为$\frac{||v|{|}_2^2}{2{\sigma }^2}$，方差为$\frac{||v|{|}_2^2}{{\sigma }^2}$。
2. 计算出$L_{M(D)||M(D^{\prime })}$小于$ϵ$的概率是$1-\delta$
   由第1步可知$L_{M(D)||M(D^{\prime })}$是服从均值为$\frac{||v|{|}_2^2}{2{\sigma }^2}$，方差为$\frac{||v|{|}_2^2}{{\sigma }^2}$的正态分布，因此我们可以写成：$L_{M(D)||M(D^{\prime })}=\frac{||v|{|}_2}{{\sigma }^2}z+\frac{||v|{|}_2^2}{2{\sigma }^2}$，其中$z\sim N(0,1)$，$pr[L_{M(D)||M(D^{\prime })}\ge ϵ]=pr[|z|\ge \frac{ϵ\delta }{||v|{|}_2}-\frac{||v|{|}_2}{2\sigma }]$，令$\sigma =\frac{{\Delta }_{2}t}{ϵ}$，则有$$pr[|z|\ge \frac{ϵ\delta }{||v|{|}_2}-\frac{||v|{|}_2}{2\sigma }]\le pr[|z|\ge t-\frac{ϵ}{2t}]\approx pr[|z|\ge t]$$根据正态分布满足$pr[z\ge v]\le \exp (-v^2/2)$则可以得出$\sigma =\frac{{\Delta }_2\sqrt{2log(2/\delta })}{ϵ}$

有关${\Delta }_2$

${\Delta }_2$衡量了l2-敏感度，其定义如下：$f:x^n\to R^k$${\Delta }_2^{(f)}=ma{x}_{x,x^{\prime }}||f(x)-f(x^{\prime })|{|}_2$，其中$x,x^{\prime }$是邻居数据。

性质

Post processing

如果$M:x^n\to y$是$ϵ$差分隐私的，$F:y\to z$是任意随机映射，那么$F\circ M$满足$ϵ$差分隐私。证明如下：
$$\frac{pr[F(M(x))=t]}{pr[F(M(x^{\prime }))=t]}=\frac{pr[M(x)\in F^{-1}(t)]}{pr[M(x^{\prime })\in F^{-1}(t)]}=\frac{{\sum }_{y\in F^{-1}(t)}pr[M(x)=y]}{{\sum }_{y\in F^{-1}(t)}pr[M(x^{\prime })=y]}\le e^{ϵ}$$

Group privacy

如果$M:x^n\to y$是$ϵ$差分隐私，$x$和$x^{\prime }$在第k个位置不同，那么对于所有$T\subset y$有$$pr[M(D)\in T]\le \exp (kϵ)pr[M(D^{\prime })\in T]$$其证明如下：
构建一个邻居数据序列:$x_0,x_1,...x_k$，依据$ϵ$差分隐私的性质，有:
$$\begin{gathered} pr[M(x_0)\in T]\le pr[M(x_1)\in T] \\ pr[M(x_1)\in T]\le pr[M(x_2)\in T] \\ ... \end{gathered}$$
连乘后得到结论$$pr[M(D)\in T]\le \exp (kϵ)pr[M(D^{\prime })\in T]$$

Basic composition

如果$M$是一系列符合$ϵ$差分隐私的函数叠加，即$M=M_k(M_{k-1}(...(M_1(x)...))$则$M$满足$kϵ$差分隐私，证明如下：
$$\frac{pr[M(x)=y]}{pr[N(x^{\prime })=y]}=\frac{{\sum }_{y_1+y_2+...y_k=y-h}\widetilde{M(x)}}{{\sum }_{y_1+y_2+...y_k=y-h^{\prime }}\widetilde{M(x^{\prime })}}\le (e^{ϵ}{)}^k=e^{ϵ}k$$

其中$\widetilde{M(x)}=pr[M_k(y_{k-1})=y_k|M_{k-1}(x)=y_{k-1}...]...pr[M_3(y_2)=y_3|M_2(y_1)=y_2,M_1(x)=y_1]pr[M_2(y_1)=y_2|M_1(x)=y_1]pr[M_1(x)=y_1]$

Advanced composition

从Basic composition引申，进一步缩小$ϵ$的范围，可以发现M满足$(ϵ\sqrt{\delta k\log (1/\delta )},k\delta +\delta )$差分隐私，即$(ϵ\sqrt{k},k\delta )$差分隐私